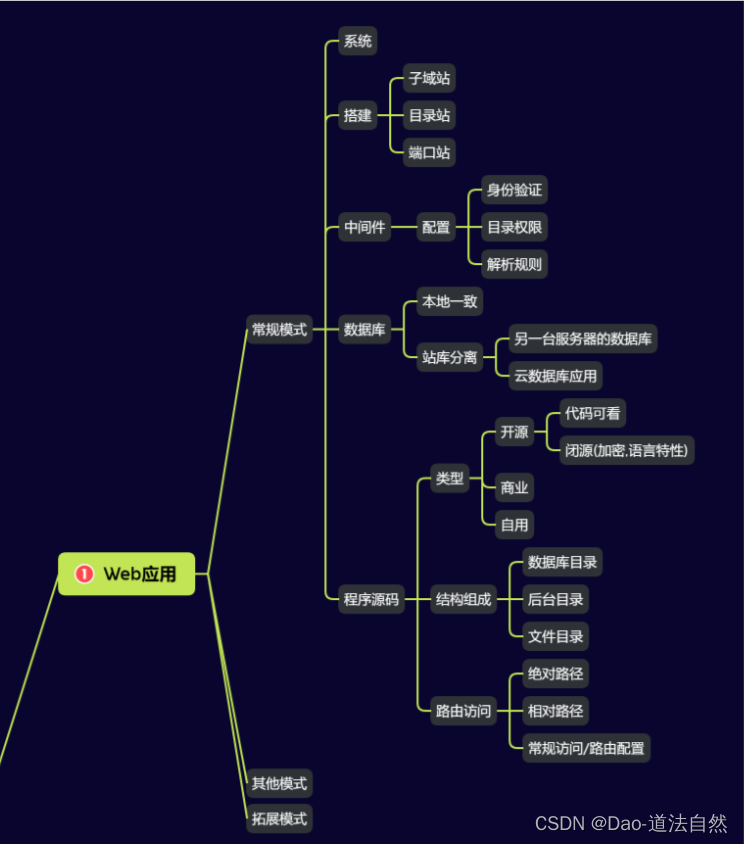
Educational Codeforces Round 71 (Rated for Div. 2)

F. Remainder Problem

题目链接

---

F. Remainder Problem

题意：

给你一个由 $500000$ 个整数（编号从 $1$ 到 $500000$ ）组成的数组 $a$ 。最初 $a$ 中的所有元素都为零。

您必须对这个数组进行两种类型的查询：

• $1$ $x$ $y$ - $a_x$ 增加 $y$ ；
• $2$ $x$ $y$ - 计算 $\sum _{i\in R(x,y)}{a}_i$ ，其中 $R(x,y)$ 是所有从 $1$ 到 $500000$ 有模 $x$ 同余 $y$ 的整数的集合。

你能处理所有的查询吗？

思路：

很好的一道根号分治题，类似的还有这道 F. Sum of Progression 。题解的F题

操作 $1$ 好说，看操作 $2$ 如何实现。发现其实就是求 $\sum a_{i\ast x+y}$ 形式的数，对这种形式，大佬说：

当步长 $x$ 很大的时候，我们其实枚举不了几次就会到边界 $n$ ，因此 $x$ 很大的时候直接枚举。而当 $x$ 比较小的时候，我们可以提前处理出结果。这里把起始位置为 $j$ ，步长为 $i$ 的这一系列位置上的数的和设为 $s[i][j]$，这样操作 $1$ 修改的时候只需要枚举步长 $i$，给所有 $s[i][x\%i]$ 加 $y$ 就可以维护住了。

而这个分界点就取为 $\sqrt{n}$，当 $x\ge \sqrt{n}$ 时，就用第一种枚举求和的方式来算。否则就直接查询 $s[i][j]$。这样每次暴力枚举的次数不会超过 $\sqrt{n}$，而每次修改的时候维护 $s$ 数组时枚举的步长也只需要枚举 $\sqrt{n}$ 次。总的时间复杂度就是枚举的复杂度加上维护 $s$ 数组的复杂度，总的复杂度不会超过 $q\sqrt{n}$。

为什么分界点取为 $\sqrt{n}$？证明只需要用均值不等式就可以了。最坏情况显然是要么操作 $1$ 修改，要么操作 $2$ 使用枚举方式查询答案。如果分界点选为 $t$ 最优，假设操作 $1$ 有 $x$ 次，那么操作 $2$ 要 $q-x$ 次。总的操作次数是 $x\ast t+(q-x)\ast \frac{n}{t}$，因为算最坏的情况，因此需要 $t=\frac{n}{t}$，否则就会按着用时最多的操作 $allin$，因此就有了 $t=\sqrt{n}$，总的时间复杂度就是 $x\ast \sqrt{n}+(q-x)\ast \sqrt{n}=q\ast \sqrt{n}$。

code：

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const int n=5e5;
const int sqn=710;int t,x,y;
ll a[n+5],s[sqn+5][sqn+5];//初值 步长int main(){int _;cin>>_;while(_--){scanf("%d%d%d",&t,&x,&y);if(t&1){a[x]+=y;for(int i=1;i<sqn;i++)s[i][x%i]+=y;}else {if(x>=sqn){ll ans=0;for(int i=y;i<=n;i+=x)ans+=a[i];printf("%lld\n",ans);}else {printf("%lld\n",s[x][y]);}}} return 0;
}