A. Moving Chips

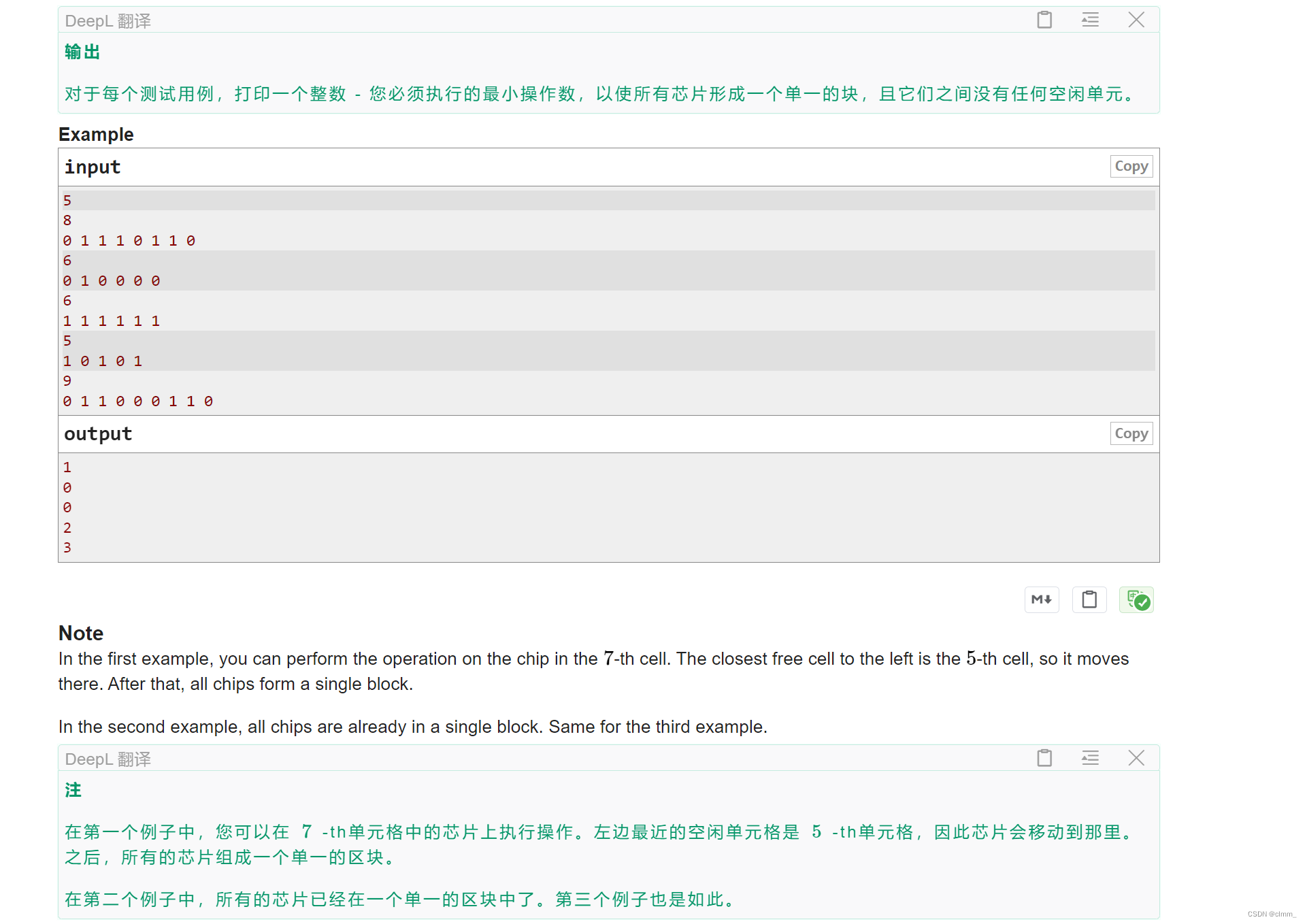
分析:先找出区间[l,r],a[l]为1第一次出现,a[r]为1最后一次出现,[l,r]以外的区间不用管。
所以我们要将[l,r]中所有1的区域块练成一块。
经过简单的样例分析发现,假设1的区域t1和区域t2间有x个0,按照最优的走法,只需要x步就能将这两块区域合成一块。
所以问题就转换成[l,r]有多少个0
int a[N];
void solve() {int n; cin >> n;int l = 1, r = n;int f = 0;rep(i, 1, n) {cin >> a[i];if (!f && a[i] == 1) {f = 1; l = i;}if (a[i] == 1) r = i;}int ans = 0;rep(i, 1, n) {if (i >= l && i <= r && a[i] == 0) ans++;}//tans;cout << ans << endl;}B. Monsters Attack!


分析:
1.当怪物1的坐标是-x,血量为t1,怪物2的坐标是x,血量为t2,那我们其实可以把他们当成同一个怪物,因为这两个怪物的威胁是相同的。所以我们就可以看成,有一个怪物在坐标x,血量为t1+t2
2.我们要优先解决离我们近的怪物,因此要对距离进行排序。我用的是map,用结构体排序也可以。
3.当前离我们最近的怪物t距离为c,假设我们在这c秒都把子弹打到怪物t身上,用一个rest记录怪物当前血量,rest>0就死了,rest<0说明伤害溢出了,没必要把所有伤害都打到这个怪物身上,应该把rest伤害留给下一个“离我们最近的怪物”。
int a[N],b[N];
void solve() {int n, k, cnt = 0; cin >> n >> k;map<int, int> mp;rep(i, 1, n) cin >> a[i];rep(i, 1, n) {cin >> b[i];if (b[i] < 0) b[i] = -b[i];mp[b[i]] += a[i];}//tans;int rest = 0;for (auto it : mp) {int c = it.first - cnt;mp[it.first] -= c * k - rest;rest = mp[it.first];if (rest > 0) {cout << "NO" << endl;return;}cnt += c;}cout << "YES" << endl;}C. Find B

分析:
对于1,我们必须要+1(题意说了必须正整数),对于大于1的数,我们可以-1。
[l,r]的长度为len,有x个数为1,len-x个数大于1。我们必须进行x次+1操作,当这len-x个数可以进行x次-1操作的话,就是YES
我们要以O(1)的时间复杂度查询到[l,r]中1的个数,所以要预处理(以类似前缀和的方法处理)。
int n, q;
int a[N], b[N], c[N];
void solve() {cin >> n >> q;rep(i, 1, n) {cin >> a[i];b[i] = b[i - 1] + a[i];c[i] = c[i - 1] + (a[i] == 1);}while (q--) {int l, r; cin >> l >> r;//tans;int len = r - l + 1;int cnt1 = c[r] - c[l - 1];int mmin = b[r] - b[l - 1] - cnt1 - (len - cnt1);if (mmin < cnt1 || len == 1) cout << "NO" << endl;else cout << "YES" << endl;}}D. Slimes

分析:前缀和,后缀和,二分我都想到了,公式也推出来了,但有这样的特殊情况{2,2,2,2},不知道怎么处理。
因为前缀和与后缀和的作用是我们可以查新,区间[l,r]的史莱姆经过互相吞噬后的大小,但如果区间[l,r]是{2,2,2,2},那么这个区间的史莱姆就不能相互吞噬(因为只有严格大于的史莱姆才能吞噬)。换言之,只要[l,r]区间的史莱姆不是全部相同的,那么[l,r]的史莱姆就可以经过相互吞噬,变成一个史莱姆。
看了题解,知道了要设pl和sl数组,来记录同一个数字连续出现了几次。
int pre[N], suf[N],a[N],pl[N],sl[N];
void solve() {int n; cin >> n;rep(i, 1, n) {cin >> a[i];pre[i] = pre[i - 1] + a[i];pl[i] = 1;if (a[i] == a[i - 1]) pl[i] += pl[i - 1];}for (int i = n; i >= 1; i--) {suf[i] = suf[i + 1] + a[i];sl[i] = 1;if (a[i] == a[i + 1]) sl[i] += sl[i + 1];}//sort(suf + 1, suf + 1 + n);//tans;rep(i, 1, n) {if (i != 1) cout << " ";int k1 = inf, k2 = inf;if(a[i-1]>a[i]||a[i+1]>a[i]){cout<<1;continue;}//往左找int l = 1, r = i;while (l <= r) {int mid = (l + r) / 2;if (suf[mid] > a[i] + suf[i] && mid+sl[mid]<i) {l = mid + 1;k1 = mid;}else {r = mid - 1;}}if (k1 != inf) k1 = i - k1;//往右找l = i + 1, r = n;while (l <= r) {int mid = (l + r) / 2;if (mid - pl[mid] > i && pre[mid] - pre[i] > a[i]) {r = mid - 1, k2 = mid;}else l = mid + 1;}if (k2 != inf) k2 = k2 - i;int ans = min(k1, k2);if (ans == inf) ans = -1;cout << ans;}cout << endl;for (ll i = 1; i <= n; ++i)a[i] = pre[i] = suf[i] = pl[i] = sl[i] = 0;}