目录

MergeSortNonR归并排序

非递归&归并排序VS快速排序 

整体思想

图解分析​

代码实现

时间复杂度

归并排序在硬盘上的应用（外排序）

---

MergeSortNonR归并排序

前面的快速排序的非递归实现，我们借助栈实现。这里我们能否也借助栈去实现归并排序呢？

非递归&归并排序VS快速排序 

• 快速排序的递归：前序递归
• 快速排序的非递归：借用栈
• 快速排序的非递归模拟递归借助栈，实际上来说，快排的非递归模拟回归的过程，就是不入栈。（实际上是没有这个回归过程的）
• 因为快速排序回归不需要处理，在分割的时候就已经处理了

---

• 归并排序的递归：后序递归
• 归并排序的非递归：直接分解
• 归并排序回归需要处理，然儿借助栈模拟非递归，根本没有回归这个过程。

---

• 处理根  左  右（前序）
• 左  右 根处理（后序）
• 借助栈模拟非递归，比较适合前序，后序需要复杂处理是不适合的。

整体思想

• 借助斐波那契数列的非递归思想
• 递归的分治是倒着推；非递归的分治是正着推（顺着往前推）
• 把整个序列直接看成分解之后的（不在去分解了）。直接合并。
• 一一合并，二二合并，四四合并等等........(❗万一这个不是2的次方数合并呢❓）
• 每小组合并之后拷贝回原数组（❗不要在每大组合并完再去拷贝❗）
• 因为是一一合并，二二合并等等。设置一个gap变量控制每大组的合并

---

每小组

• 设置begin1&end1&begin2&end2控制两个区间的序列的合并
• 两段有序序列的合并
• 拷贝 | 每小组合并之后拷贝回原数组（❗不要在每大组合并完再去拷贝❗）
• ❗区间必须变化起来

---

每大组

• 写入循环for
• 完成每gap组的合并拷贝
• 循环使❗区间必须变化起来

---

整体

• gap变化起来
• 结束条件：< n

---

易错点：

• 每小组合并完之后再去拷贝
• 区间合并的起始位置&结束位置&拷贝的长度问题。
• 合并的组数不一定都是2的次方倍，越界问题。（可以尝试打印区间来查看越界问题）
• 越界问题存在三种情况（begin1=i<n不会越界）

1. end1（后面两个肯定越界，第一序列存在数，第二序列不存在数）
2. begin2（end2肯定越界，第二序列不存在数）
3. end2（可能第二序列区间还存在数）

图解分析​​​​​​​​​​​​​​ 

 

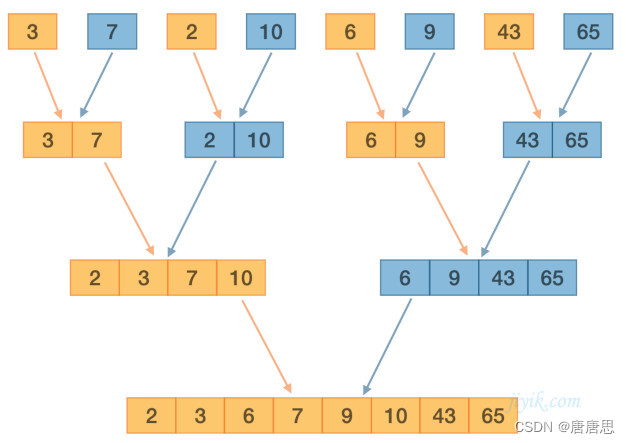
代码实现

#include<stdio.h>
#include<stdlib.h>
#include<string.h>//0          n-1
void MergeSortNonR(int* a, int begin, int end, int* tmp)
{//直接看成分割完合并的int gap = 1;//整体while (gap < end + 1){//每组for (int i = 0; i < end + 1; i += 2 * gap){//每小组int begin1 = i;//不会越界int end1 = i + gap - 1;//会越界int begin2 = i + gap;int end2 = i + 2 * gap - 1;int j = i;//越界结束=n if (end1 >= end + 1 || begin2 >= end + 1){break;}//越界修改if (end2 >= end + 1)//=注意{end2 = end;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else//>={tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}//begin1变了大哥memcpy(a + i, tmp + i, sizeof(int) * (end2-i+1));}printf("\n");gap = gap * 2;}
}int main()
{int a[] = { 10,6,7,1,3,9,4,2,9,8,7 };int n = sizeof(a) / sizeof(a[0]);int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}MergeSortNonR(a, 0, n - 1, tmp);PrintSort(a, n);free(tmp);return 0;
}

时间复杂度

时间复杂度：O（N*logN) 

归并排序在硬盘上的应用（外排序）

• 内部排序：数据元素全部放在内存中的排序。
• 外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。（硬盘）
• 归并排序既是内排序，也是外排序。

• ---

  内存和硬盘的区别？
• 为什么归并排序可以是外排序，其他排序只能是内排序？
• 为什么数据要放到硬盘里面？
• 大量的数据在文件中保存，如果用归并排序使其有序？

🙂感谢大家的阅读，若有错误和不足，欢迎指正。关于归并排序作为外排序在文件中的应用，后面的补充内容会详细讲解。