2月28日代码随想录二叉搜索树中的众数

摸了一个寒假了，得赶一赶了

251.二叉搜索树中的众数

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

示例 1：

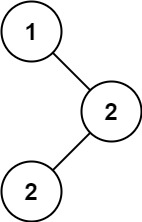
输入：root = [1,null,2,2]
输出：[2]

示例 2：

输入：root = [0]
输出：[0]

提示：

树中节点的数目在范围 [1, 104] 内
-105 <= Node.val <= 105

进阶：你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）

思路

哈希表中序遍历

还记得二叉搜索树的遍历用的是二叉树的中序遍历的特性，在遍历二叉搜索树时是从小到大的顺序遍历的，所以我们需要在遍历的过程中找到所有的众数并且加入结果中，在遍历过程中将每个数的出现次数存入HashMap，并记录最大值，最后遍历hashmap并将键值为最大值的所有key加入ArrayList，最后转为数组。

class Solution {public int[] findMode(TreeNode root) {Map<Integer, Integer> map = new HashMap<>();Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;int max = 0;while (cur != null || !stack.isEmpty()) {if (cur != null) {stack.push(cur);cur = cur.left;} else {cur = stack.pop();map.put(cur.val, map.getOrDefault(cur.val, 0) + 1);if (map.get(cur.val) > max)max = map.get(cur.val);cur = cur.right;}}List<Integer> modes = new ArrayList<>();for (Map.Entry<Integer, Integer> entry : map.entrySet()) {if (entry.getValue() == max) {modes.add(entry.getKey());}}return modes.stream().mapToInt(i -> i).toArray();}}

此处将ArrayList转换为int数组使用了java流的方法：

但是这个解法我写的非常难绷，差点气笑了，纯纯狗屎。

中序遍历法（真）

官方题解第一句话直接否定了我的若只解法，哈哈，真是一场酣畅淋漓的破防啊，活个屁啊，跳了

其实也没高明到哪里去，只是在遍历的过程中更新答案数组。用base记录当前数字，count记录当前数字重复次数，用maxCount记录当前已经扫描过的数中出现最多的数的次数，answer代表众数数组。每次扫描到一个新元素：

首先更新base和count：

如果该元素与base相同，那么count自增1；

如果不同，base更新为当前数字，count复位为1。

然后更新maxcount：

如果count=maxcount，那么说明当前数字也为当前众数，将base加入answer

如果count>maxcount，那么将answer清空，再将base加入answer。

    class Solution {List<Integer> answer=new ArrayList<>();int base,count,maxCount;public int[] findMode(TreeNode root) {dfs(root);int[] mode=new int[answer.size()];for(int i=0;i<answer.size();++i){mode[i]=answer.get(i);}return mode;}public void dfs(TreeNode node){if(node==null){return;}dfs(node.left);update(node.val);dfs(node.right);}public void update(int i){if(i==base){count++;}else {count=1;base=i;}if(count==maxCount){answer.add(base);}if(count>maxCount){maxCount=count;answer.clear();answer.add(i);}}}

以后遍历二叉树还是写递归吧，看着就清爽。

Morris中序遍历

最后来解决进阶问题：如何将空间复杂度控制在O(1)?

从前两个方法的代码中我们可以发现，主要的空间消耗在于中序遍历，不管是递归回溯或者是迭代法用栈存储返回点，都需要付出额外的空间代价。

Morris中序遍历：

其实没太看懂。

 class Solution {List<Integer> answer = new ArrayList<>();int base, count, maxCount;public int[] findMode(TreeNode root) {TreeNode cur = root, pre = null;while (cur != null) {if (cur.left == null) {update(cur.val);cur = cur.right;continue;}pre = cur.left;while (pre.right != null && pre.right != cur) {pre = pre.right;}if (pre.right == null) {pre.right = cur;cur = cur.left;} else {pre.right = null;update(cur.val);cur = cur.right;}}int[] mode = new int[answer.size()];for (int i = 0; i < answer.size(); ++i) {mode[i] = answer.get(i);}return mode;}public void update(int i) {if (i == base) {count++;} else {count = 1;base = i;}if (count == maxCount) {answer.add(base);}if (count > maxCount) {maxCount = count;answer.clear();answer.add(i);}}}

懂了吗？