插值
插值(Interpolation)是数学和计算科学中的一个重要概念,它指的是通过已知的一系列数据点,构造一个函数或曲线,并据此估计未知数据点的值。这个过程通常发生在已知数据点之间,用于预测或估算在这些已知点之间的某个位置的值。
插值有多种方法,包括线性插值、多项式插值、样条插值(如立方样条插值)、径向基函数插值等。选择哪种插值方法取决于具体的应用场景、数据点的分布、所需的精度和计算效率等因素。

逼近
逼近(Approximation)是数值分析和函数逼近论中的一个重要概念。它的目的是找到一个相对简单的函数(称为逼近函数或近似函数),该函数在某种度量下尽可能地接近给定的复杂函数。逼近通常用于处理那些难以直接计算或分析的复杂函数。
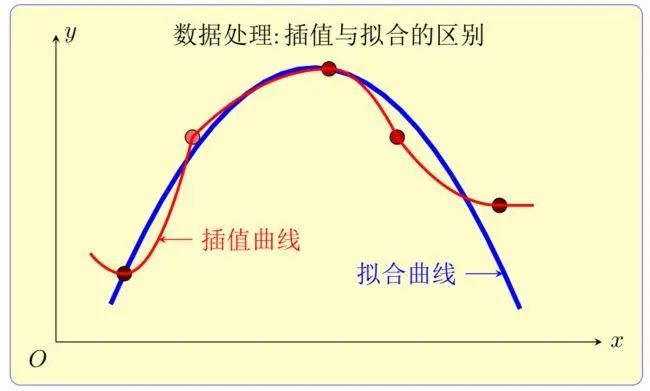
逼近与插值有所不同。插值要求逼近函数必须通过所有给定的数据点,而逼近则只要求逼近函数在某种意义下接近这些点,并不一定要通过它们。逼近通常用于处理无穷多个数据点的情况,或者当数据点之间存在噪声时。
逼近的方法有很多,包括多项式逼近、三角多项式逼近、有理函数逼近、样条逼近、小波逼近等。选择哪种逼近方法取决于被逼近函数的性质、逼近的精度要求、计算复杂度等因素。
拟合
拟合(Fitting)是数学和统计学中用于描述一个模型(通常是一个函数或一组参数)如何最好地适应给定数据的过程。拟合的目的是找到一个模型,该模型能够尽可能准确地描述数据中的关系或模式。这种关系可以是线性的,也可以是非线性的。
拟合通常涉及到最小化某种误差度量,例如均方误差(Mean Squared Error)或最大似然估计(Maximum Likelihood Estimation)。拟合的过程可以使用多种数学方法来实现,包括最小二乘法、最大似然法、梯度下降法等。
拟合与插值和逼近有些相似,但也有所不同。插值要求模型必须通过所有数据点,而逼近则要求模型在某种度量下尽可能接近所有数据点。相比之下,拟合更注重模型的整体性能和预测能力,而不仅仅是模型与数据点的匹配程度。因此,拟合通常用于构建能够预测新数据的模型。
拟合在许多领域都有广泛应用,包括统计建模、机器学习、数据分析、图像处理等。例如,在机器学习中,线性回归和逻辑回归等模型就是通过拟合训练数据来构建预测模型的。
光顺
在图形学和几何造型中,光顺通常指的是曲线或曲面的连续性和平滑性。一个光顺的曲线或曲面应该看起来自然流畅,没有明显的拐点或折痕,曲率变化均匀且连续。这种光顺性对于提高模型的真实感和视觉效果至关重要。