oppo手机备忘录记录怎么转移到华为手机?使用oppo手机已经有三四年了,因为平时习惯,在手机系统的备忘录中记录了很多重要的笔记,比如工作会议的要点、读书笔记、购物清单、朋友的生日提醒等。这些记录对我来说非常重要,我可以通过查看了解哪些事情做了,哪些事情没做,或者是即将要做的。
最近,想换个华为手机,但是,担心oppo手机备忘录无法转移到华为手机中,导致我会丢失这些重要的信息。我尝试使用了手机搬家助手软件,但很遗憾地发现,这类软件不支持将系统备忘录、便签、笔记等内容直接从旧手机传输到不同品牌的另一个手机中。
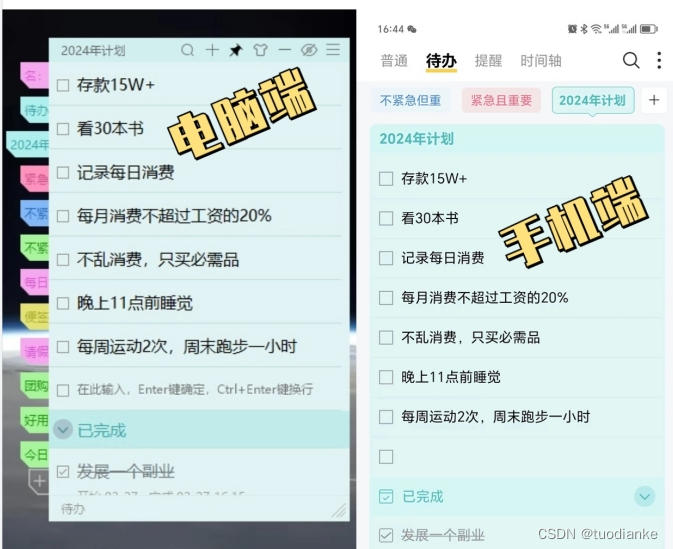
这个时候,无意中发现了好用便签这款桌面便签APP,它可以帮助我们轻松地在不同品牌的手机之间转移备忘录和便签内容。好用便签支持在华为、vivo、小米、OPPO、苹果等各种手机端使用,并且能实现内容的多端实时同步。这意味着,我只需将oppo手机的备忘录内容转移到好用便签中,然后在新的华为手机上登录好用便签帐号就可以查看到自动同步过来的备忘录内容。
考虑到oppo手机的备忘录不支持一键导出内容,我选择在oppo手机上安装好用便签,然后逐条复制备忘录内容并粘贴到云便签中保存。这个过程虽然有些繁琐,但考虑到能够顺利转移我的所有重要记录,这一切都是值得的。
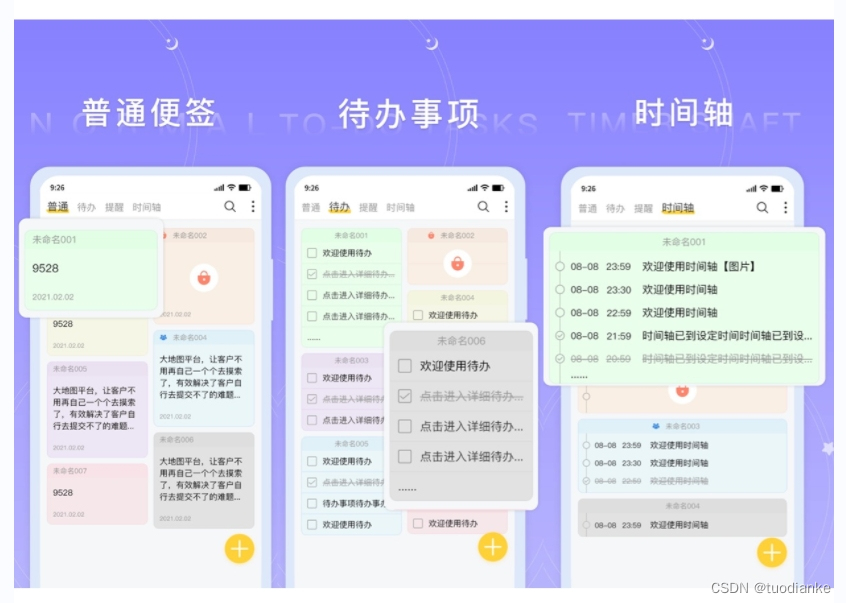
当我在华为手机上打开好用便签时,我惊喜地发现,之前从oppo手机上转移过来的备忘录内容已经自动同步到了华为手机中的好用便签中了,方便我继续在新手机上使用这些备忘录内容。因此,我打算以后直接使用好用便签来记录各种信息,这样无论将来我更换到哪款手机,都无需再为备忘录内容的转移而烦恼,直接在新手机上使用好用便签即可,真正实现了记事内容的无缝迁移和同步。
最后,现在大家是否已经知道oppo手机备忘录记录怎么转移到华为手机了呢,不管你是什么品牌的手机,好用便签都支持兼容,再也不用担心数据丢失的问题,哪怕是手机突然坏了也不用担心了。