本篇来介绍信号量与PV原语的一些知识,并介绍其在前趋图上的应用分析。本篇的知识属于操作系统部分的通用知识,在嵌入式软件开发中,同样会用到这些知识。
1 信号量
信号量是最早出现的用来解决进程同步与互斥问题的机制(可以把信号量视为一个加锁标志位,实现对临界资源互斥的访问)。
信号量是一个整数:
- 当信号量S>=0时,代表可供并发使用的资源数量
- 当信号量S<0时,代表已经没有可用资源,S的绝对值表示当前等待该资源的进程数
利用信号量可以实现进程的互斥与同步
2 PV原语
2.1 P原语(wait)
P原语(申请资源,相当于wait,阻塞进程)操作的动作是:
- sem减1
- 若sem减1后仍>=0,则执行P操作的进程继续执行
- 若sem减1后<0,则执行P操作的进程被阻塞后进入与该信号相对应的队列中,然后转进程调度
2.2 V原语(signl)
V原语(释放资源,相当于signal,激活进行)操作的动作是:
- sem加1
- 若sem加1后>0,则执行V操作继续执行
- 若sem加1后仍<=0(表明有进程阻塞在该类资源上),则从该信号的等待队列中唤醒一等待进程,然后再返回原进程继续执行或转进程调度
注意:PV操作对于每一个进程来说,都只能进行一次,而且必须成对使用。在PV原语执行期间不允许有中断的发生。

2.3 P、V操作
PV原语的执行顺序:
- 执行P操作,信号量减一
- 然后进行对共享资源的访问
- V操作,信号量加一
PV操作中关于信号量的计算:
某系统有n个进程,共享资源R,R是可用数为m,其中n>=m。若采用PV操作,则信号量S的取值范围是多少?
分析:
- 信号量的最大值,即可用资源的数据,即m
- 信号量的最小值,即最多能阻塞的进程数量,然后取负数,本例中,最大阻塞数为n-m
- 所以,信号量S的取值范围是 -(n-m)~m
3 信号量与PV操作的应用
3.1 实现进程互斥
为使多个进程互斥的访问某临界资源(例如一台打印机):
- 须为该资源设置一个互斥信号量mutex,并设其初值为1
- 然后各进程访问资源的临界区CS置于wait(mutx)和signal(mutex)之间即可
semaphore mtuex = 1; //表示打印机(互斥/共享资源)void process1() //进程1
{//...wait(mutx); //P操作,信号量-1//使用打印机signal(mutex); //V操作,信号量+1//...
}void process2() //进程2
{//...wait(mutx);//P操作,信号量-1//使用打印机signal(mutex);//V操作,信号量+1//...
}
这里简单分析一下
-
只有一台打印机,所以信号量初值是1
-
wait(mutx),即P操作,信号量减1,例如:
- 当第一个进程使用打印机时,信号量减为0,没有进程阻塞
- 当第二个进程也使用打印机时,信号量再减1变为-1,小于0了,说明有进程阻塞(就是第二个进程阻塞)
- 当第三个进程也使用打印机时,信号量再减1变为-2,也小于0了,说明有进程阻塞(就是第三个进程阻塞)
-
signal(mutex),即V操作,信号量加1,例如:
- 当第一个进程使用打印机完毕时,信号量加1变为-1,仍小于0,说明激活一个进程后,仍有进程阻塞(例如第二个进程可以使用打印机了,第三个进程仍在等待)
- 当第二个进程使用打印机完毕时,信号量加1变为0,说明激活一个进程后,没有进程阻塞(第二个进程可以使用打印机了)
- 当第三个进程使用打印机完毕时,信号量加1变为1
3.2 实现前趋关系(前趋图)
这里先简单介绍下前趋图:
前趋图是为了描述一个程序的各部分间的依赖关系,或者是一个大的计算的各个子任务间的因果关系的图示。
前趋图中的每个结点可以表示一条语句、一个程序段或一个进程
结点间的有向边表示两个结点之间存在的偏序(Partial Order)或前趋关系
3.2.1 例子1
进程P1P5的前趋图如下所示,若用PV操作控制进程P1P5并发执行的过程,需要设置5个信号量S1~S5,且信号量的初值都是0。
根据以上描述,下图中的a~e处分别该填什么:

分析,根据文字描述,对照图中信息,可先将P(S1)和P(S3)在图中标注出来,进而可推出信号量S1和S3以及V操作V(S1)和V(S3)。
然后假设P1到P3使用的信号量S3,P3到P5使用的信号量S4,P4到P5使用的信号量S5,即可推导出剩余的PV操作。

3.2.2 例子2
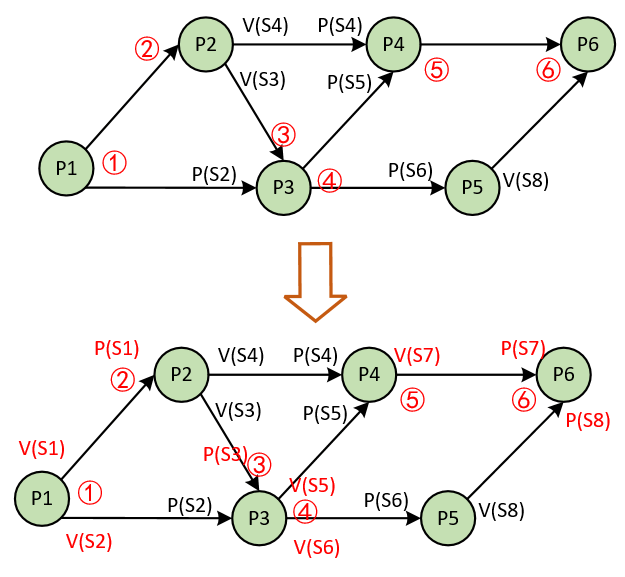
进程P1P6的前趋图如下所示,若用PV操作控制进程P1P6进程同步与互斥的程序如下,则呈现中中的①~⑥处分别该填什么:

分析:根据程序中的描述,对照图中信息,可先将程序中已表示的PV操作标注出来,并标注出①~⑥在图中的位置。
然后假设P1到P2使用的信号量S1,P4到P6使用的信号量S7,P5到P6使用的信号量S8,即可推导出剩余的PV操作
4 总结
本篇介绍了信号量与PV原语的基础知识点,并介绍了PV操作的一些应用,实现进程互斥和实现前趋关系,前趋关系中使用前趋图来实例分析PV操作影响信号量变化的具体运行过程。