8. KNN

8.1 简述一下KNN算法的原理?
一句话概括:KNN的原理就是当预测一个新的值x的时候,根据它距离最近的K个点是什么类别来判断x属于哪个类别
工作原理:存在一个样本数据集合,也称作为训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一个数据与所属分类的对应关系。输入没有标签的新数据后,将新的数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本最相似数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
3个主要因素是:k值选择,距离度量,分类决策。
8.2 如何理解KNN中的k的取值?
K值的重要性需要先看一下距离度量,要度量空间中点距离的话,有好几种度量方式,比如常见的曼哈顿距离计算,欧式距离计算等等。不过通常KNN算法中使用的是欧式距离,这里只是简单说一下,拿二维平面为例,,二维空间两个点的欧式距离计算公式如下:![]()
将其拓展到多维空间则为下图
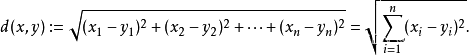
KNN算法最简单粗暴的就是将预测点与所有点距离进行计算,然后保存并排序,选出前面K个值看看哪些类别比较多。但其实也可以通过一些数据结构来辅助,比如最大堆。
由距离度量可知,K的取值比较重要,该如何确定K取多少值好呢?答案是通过交叉验证(将样本数据按照一定比例,拆分出训练用的数据和验证用的数据,比如6:4拆分出部分训练数据和验证数据),从选取一个较小的K值开始,不断增加K的值,然后计算验证集合的方差,最终找到一个比较合适的K值。
8.3 在kNN的样本搜索中,如何进行高效的匹配查找?
线性扫描(数据多时,效率低) 构建数据索引—