openGL 透视投影矩阵
什么是透视投影?
模型都是3D的,但屏幕是2D的。如何将3D空间投影到2D平面,还能保持深度的视觉效果?在OpenGL中,采用透视投影矩阵作用顶点来实现,即完成缩放、选择、位移之后,进行透视投影的操作。

投影矩阵原理
投影矩阵用于投影变换,投影变换是三维场景中的物体正确渲染到二维屏幕的重要过程之一。在透视矩阵中,有几个重要元素:视场角、成像设备的宽高比、场景中能看到的最近距离以及最远距离,通过这几个参数可以定义一个视锥体对象,从而模拟人眼或者相机的在三维空间中的成像原理,通常有这个几个值就可以构造一个4x4的矩阵,通过OpenGL提供的接口设置即可。参数(near=n, far=f, left=l, right=r, top=t, bottom=b),对应矩阵如下:
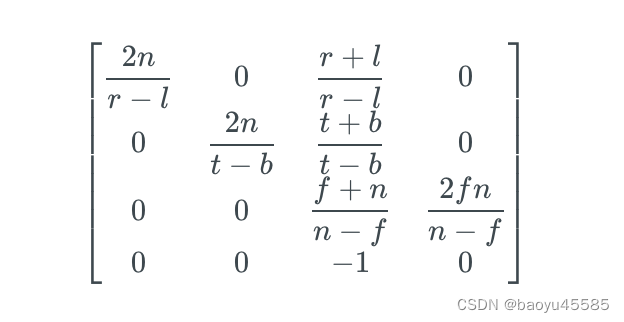
假设下图是Z方向投影到屏幕的立体图如下 ,根据上面矩阵参数可以推到为图的对应参数
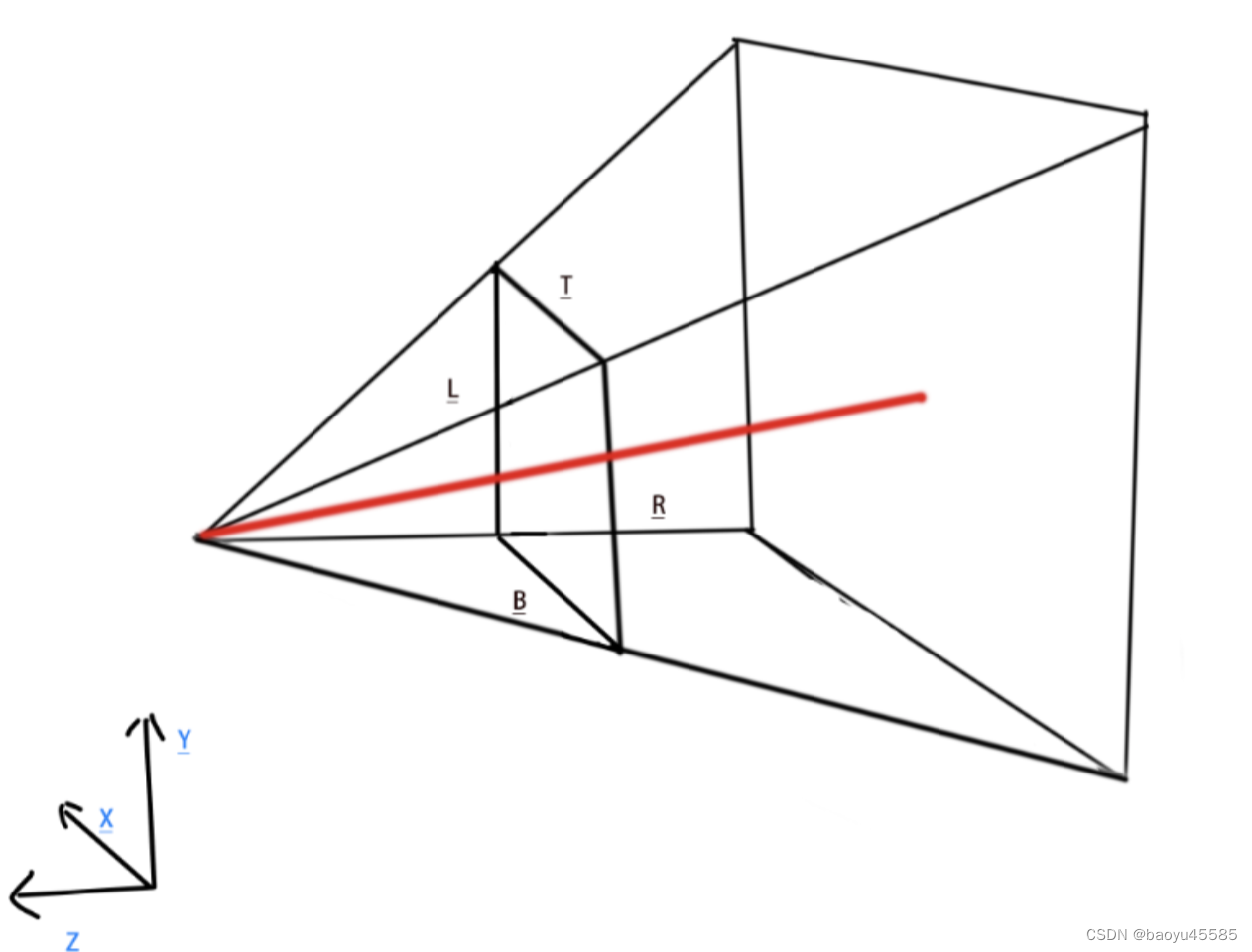
侧视图看
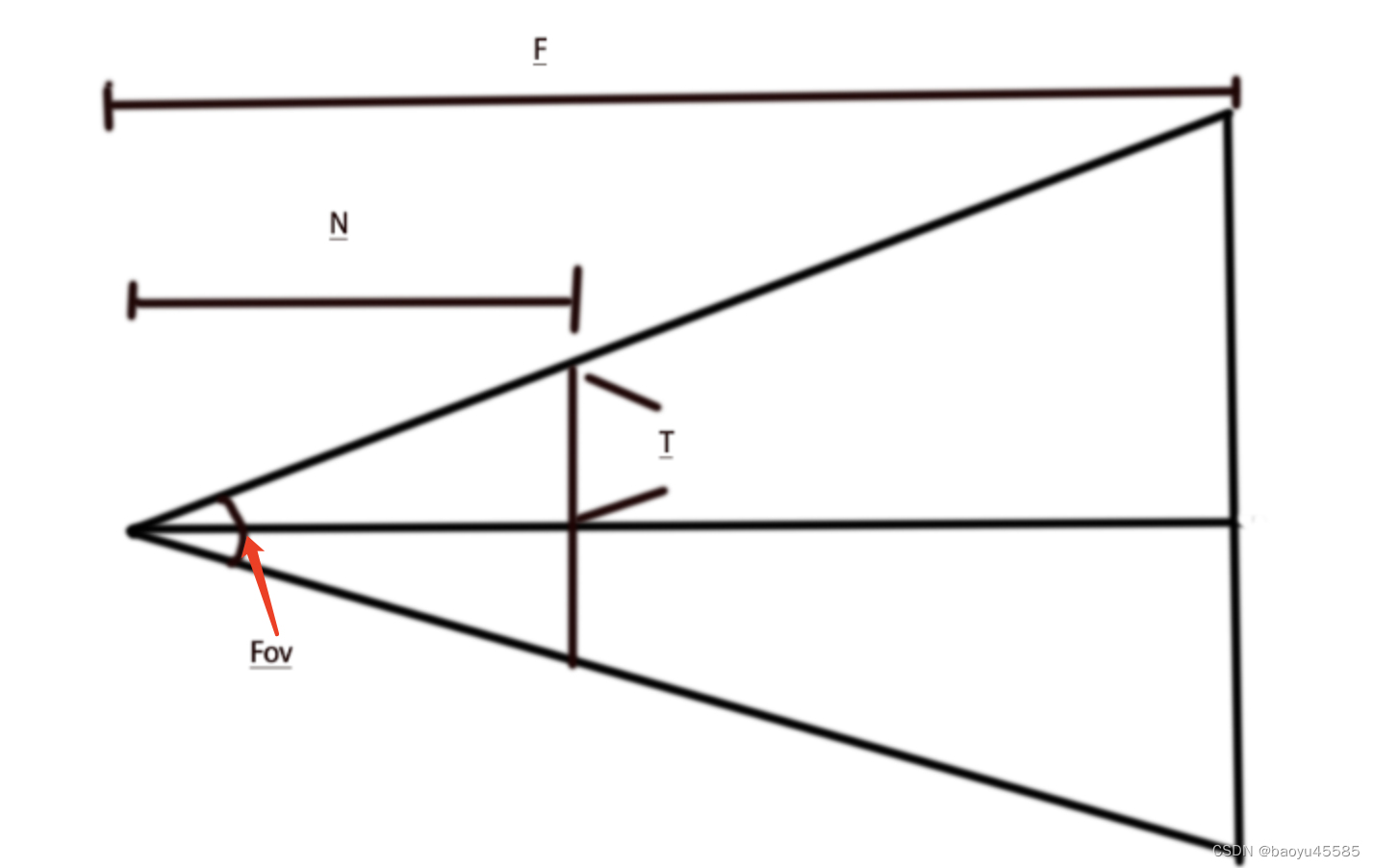
根据上图推出对应参数技术
- 1.aspect:屏幕宽高比m_screenWidth / m_screenHeight
- 2.n:近截面z轴坐标
- 3.f :远截面z轴坐标
- 4.fov角度
- 5.我们可以求出t的长度t=n*tan(fov/2)
- 6.t = n * Math.tan(fov / 2);// n*tan(fov / 2)=T(勾股定理,计算直角边)
- 7.b = -t;
- 8.r = aspect * t;
- 9.l= -r;
上面推到的对应矩阵参数,为什么要做这样矩阵,视锥体视图进一步的介绍,更加深刻认识和理解还是图解,下面透视投影进行点位和对应参数,如下:
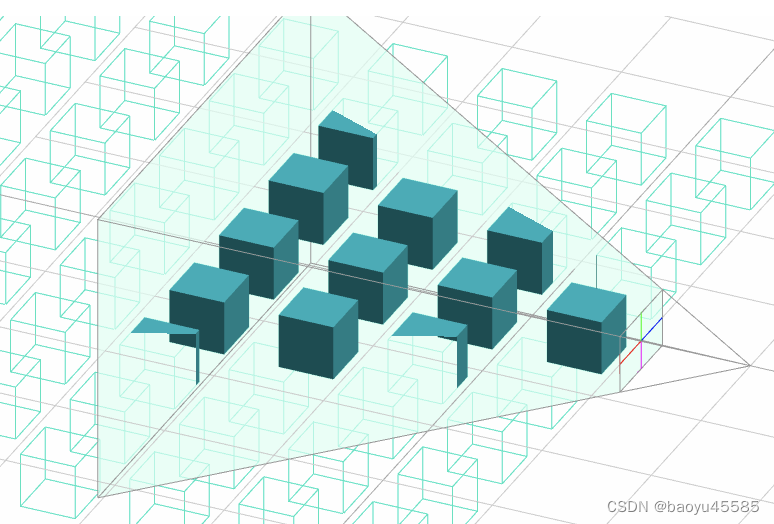
对称摄像机在相机空间中 YZ 平面上的视锥体视图。请注意,顶部(t)、底部(b)和近裁剪面距离(n)都决定了垂直视野角(θ)。远处平面上的 Y 范围是通过比率 f/n 计算的,因为对于原点/近处三角形和原点/远处三角形来说,这些角度都是相同的。由下图可以计算相关点位
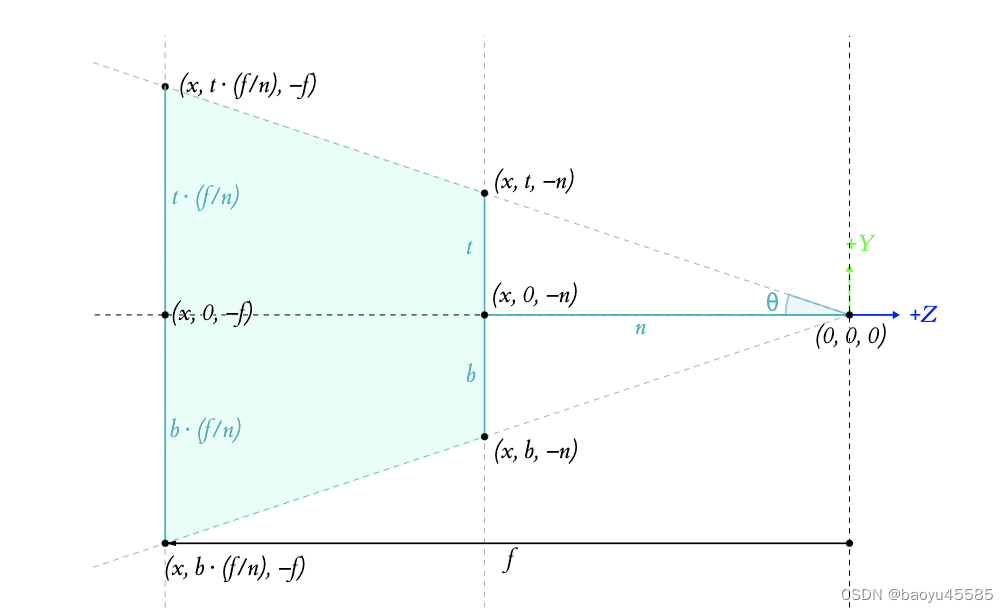
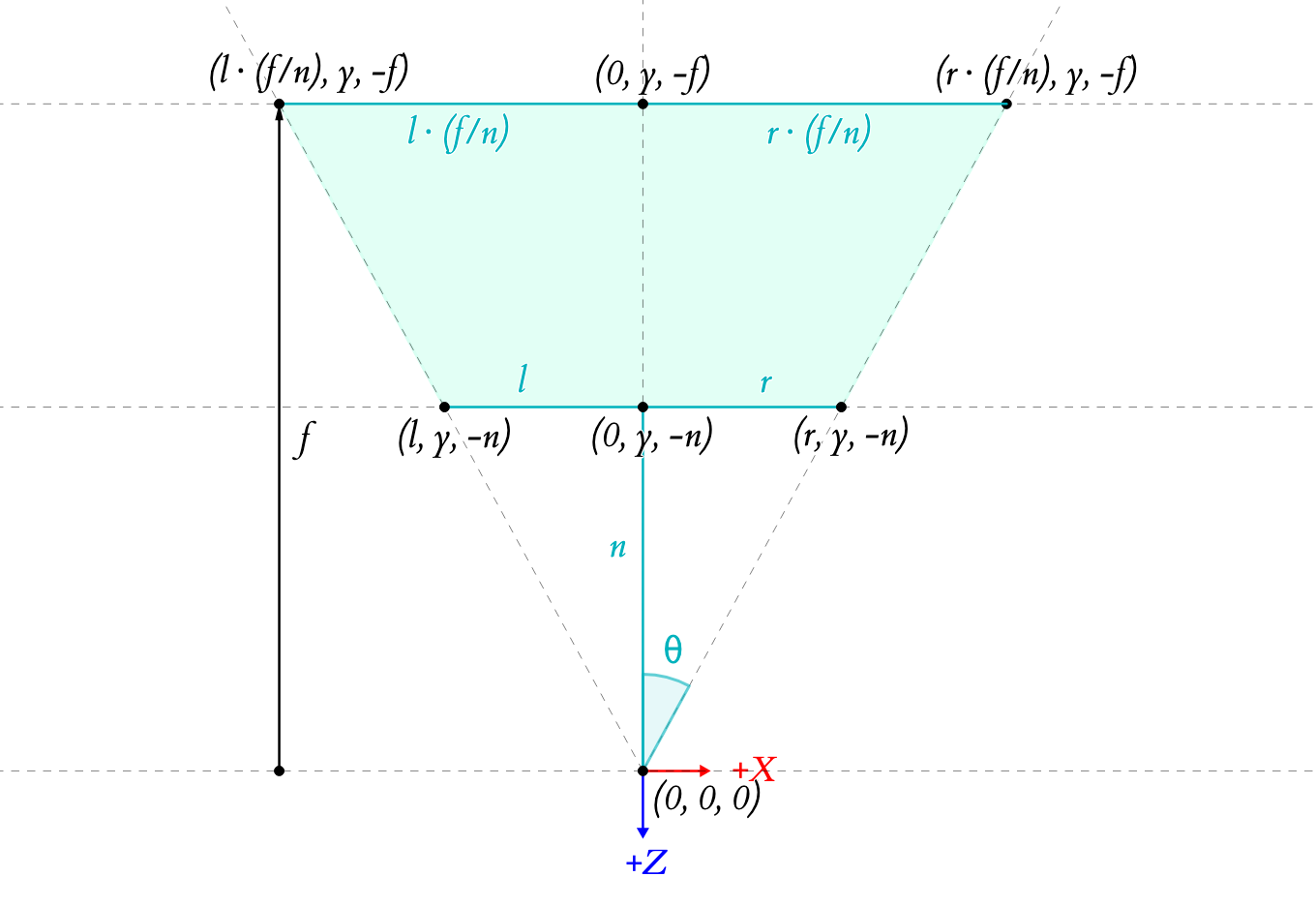
对称摄像机在相机空间中 XZ 平面上的视锥体视图。与图1几乎相同,只是使用左侧(l)和右侧(r)的视锥体范围。
t = n * Math.tan(fov / 2);b = -t;r = aspect * t;l= -r;
通过上面知识和原理,就可以实现对应代码生成4x4的矩阵
const double DEG2RAD = 3.14159265 / 180;:该行定义了一个常量 DEG2RAD,用于将角度转换为弧度float tangent = tanf(fFov / 2.f * DEG2RAD);:在这行中,fFov 表示视场角(Field of View),它通常以角度表示。首先,将 fFov 视场角转换为弧度,并取其一半。
m3dLoadIdentity44对应的初始化可以查看这篇-OpenGL 位移、缩放、旋转原理
void m3dMakePerspectiveMatrix(M3DMatrix44f mProjection, float fFov, float fAspect, float zMin, float zMax)
{m3dLoadIdentity44(mProjection); // Fastest way to get most valid values already in placeconst double DEG2RAD = 3.14159265 / 180;float tangent = tanf(fFov / 2.f * DEG2RAD); // tangent of half fovYfloat height = zMin * tangent; // half height of near planefloat width = height * fAspect; // half width of near planefloat l = -width, r = width, b = -height, t = height, n = zMin, f = zMax;// params: left, right, bottom, top, near, farmProjection[0] = 2 * n / (r - l);mProjection[5] = 2 * n / (t - b);mProjection[8] = (r + l) / (r - l);mProjection[9] = (t + b) / (t - b);mProjection[10] = -(f + n) / (f - n);mProjection[11] = -1;mProjection[14] = -(2 * f * n) / (f - n);mProjection[15] = 0;
}