【李沐论文精读】GAN精读

论文：Generative adversarial nets

参考：GAN论文逐段精读、生成对抗网络、李沐视频精读系列

一、介绍

什么是GAN?

GAN(Generative adversarial network，生成对抗网络），它由生成器G（Generator Neural Network）和判别器D（Discriminator Neural Network）组成，生成器G负责生成样本，判别器D负责判断生成器生成的样本是否为真。生成器要尽可能迷惑判别器，而判别器要尽可能区分生成器生成的样本和真实样本。

生成器G从给定噪声中（一般是指均匀分布或者正态分布）采样来合成数据，判别器D用于判别样本是真实样本还是G生成的样本。G的目标就是尽量生成真实的图片去欺骗判别网络D，使D犯错；而D的目标就是尽量把G生成的图片和真实的图片分别开来。二者互相博弈，共同进化，最终的结果是D(G(z)) = 0.5，此时G生成的数据逼近真实数据（图片、序列、视频等）。

最后我们希望生成器G生成的样本能“以假乱真”。

二、相关工作（Related Work）

之前的生成模型总是想构造一个分布函数出来，同时这些函数提供了一些参数可以学习。这些参数通过最大化对数似然函数来求解。这样做的缺点是，采样一个分布时，求解参数算起来很难，特别是高维数据。因为这样计算很困难，所以最近有一些Generative Machines，不再去构造分布函数，而是学习一个模型来近似这个分布。前者真的是在数学上学习出一个分布，明明白白知道数据是什么分布，里面的均值方差等等到底是什么东西。而GAN就是通过一个模型来近似分布的结果，而不需要构造分布函数。这样计算起来简单，缺点是不知道最终的分布到底是什么样子。

DBM 和我们的 generative models 有什么区别？

DBM：一定要学分布，知道均值、方差等一系列参数
GAN：用一个模型学习你想要的结果，答对题就行。

三、GAN的目标函数与求解

3.1 目标函数

GAN最简单的框架就是模型都是MLP。

(1) 生成器G是要在数据x上学习一个分布 $p_g(x)$ ，其输入是定义在一个先验噪声 $z$ 上面， $z$ 的分布为 $p_{z}(z)$ 。生成模型G的任务就是用MLP把 $z$ 映射成 $x$ 。

比如图片生成，训练图片是224*224，每个像素是一个随机变量，那么x就是一个50176维的随机变量，变量每个元素都是 $p_g(x)$ 控制的。
不管最终x如何生成，假设不同的生成图片其实就是那么100来个变量控制的，而MLP理论上可以拟合任何一个函数。那么我们就构造一个100维的向量，MLP强行把z映射成x。所以z可以先验的设定为一个100维向量，其均值为0，方差为1，呈高斯分布。（这样算起来简单）
随机设定z为100维向量的缺点，就是MLP并不是真的了解背后的z是如何控制输出的，只是学出来随机选一个比较好的z来近似x，所以最终效果也就一般。
$G$ 的可学习参数是 $G(z;\theta _{g})$

(2) 判别器D是输出一个标量（概率），判断其输入是G生成的数据/图片，还是真实的数据/图片。

D的可学习参数是 $D(x;\theta_{d})$
对于D，真实数据label=1，假的数据label=0

(3) 两个模型都会训练

G的目标是希望生成的图片“越接近真实越好，D(G(z))变大接近1，也就是最小化 $log(1-D(G(z)))$ ，记作 $\underset{G}{min}$
D的目标是最大化 $logD(x)$ ，记作 $\underset{D}{max}$

由此最终目标函数公式如下：

其中，E代表期望， $X\rightarrow P_{data}$ 代表分布为 $P_{data}$ 的真实样本， $Z\rightarrow p_z(z)$ 代表分布为 $P_{z}(z)$ 的生成样本。公式中的 $\underset{G}{min}\, \underset{D}{max}$ 则是对抗网络的训练。

假设x和z都是一维向量，且z是均匀分布，模型训练过程可以表示为：

如上图所示：虚线点为真实数据分布，蓝色虚线是判别器D的分布，绿色实线为生成器G的分布。初始训练出生成器网络G和判别器网络D；从a到d是我们希望的训练过程。

a. 生成器从均匀分布学成绿色实线表示的高斯分布，这时候判别器还很差；
b. 判别器学成图b所示的分布，可以把真实数据和生成数据区别开来；
c.生成器波峰靠向真实数据波峰，自然就使得判别器难以分辨了；辨别器为了更准，其分布也往真实数据靠拢；
d.最终训练的结果，生成器拟合真实分布，判别器难以分辨，输出概率都为0.5 。

3.2 求解过程

算法迭代过程如下：

k是一个超参数，不能太小也不能太大。要保证判别器D可以足够更新，但也不能更新太好。

如果D更新的不够好，那么G训练时在一个判别很差的模型里面更新参数，继续糊弄D意义不大；
如果D训练的很完美，那么 $log(1-D(G(z)))$ 趋近于0，求导结果也趋近于0，生成器难以训练。

整体来说GAN的收敛是很不稳定的，所以之后有很多工作对其进行改。

四、理论结果

4.1 全局最优解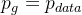 $p_{g}=p_{data}$

这部分需要证明目标函数 $\underset{G}{min}\underset{D}{max}V(D,G)$ 有最优解，且这个解当且仅当 $p_{g}=p_{data}$ 时成立，也就是生成器学到的分布等于真实数据的分布。

(1) 固定生成器G，最优的辨别器应该是：

*表示最优解
$p_g$ 和 $p_{data}$ 表示x在生成器拟合的分布里面，和真实数据的分布里面，它的概率分别是多少。
当 $p_{g}=p_{data}$ 时，结果为1/2，表示两个分布完全相同，最优的判别器也无法将其分辨出来。
这个公式的意义是，从两个分布里面分别采样数据，用目标函数 $\underset{G}{min}\underset{D}{max}V(D,G)$ 训练一个二分类器，如果分类器输出的值都是0.5，则可以认为这两个分布是完全重合的。在统计学上，这个叫two sample test，用于判断两块数据是否来自同一分布。

(2) 把D的最优解代回目标函数，目标函数之和G相关，写作C(G)并最小化这一项就行。

(3)证明当且仅当 $p_{g}=p_{data}$ 时有最优解 $C(G)=-log4$ 。

上式两项可以写成KL散度，即：

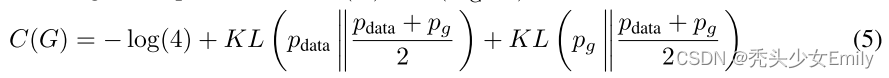
又因为JS散度定义为：

$JSD(P\parallel Q)=\frac{1}{2}D(P\parallel M)+\frac{1}{2}D(Q\parallel M)$

$M=\frac{1}{2}(P+Q)$

简化为： $C(G)=-log4+2\cdot JSD(p_{data}\parallel p_g)$
要求 $minC(G)$ ，只有最后一项等于0时成立（JS散度≥0），此时 $p_{g}=p_{data}$ 。

ps：JS散度跟KL散度的区别是前者是对称的， $p_g$ 和 $p_{data}$ 可以互换，而后者不对称。

4.2 收敛证明

这部分证明了：给定足够的训练数据和正确的环境，在算法1中每一步允许D达到最优解的时候，对G进行下面的迭代：

训练过程将收敛 $p_{g}=p_{data}$ ，此时生成器G是最优生成器。

五、结论

GAN的优点：

比其它模型生成效果更好（图像更锐利、清晰）。
GAN能训练任何一种生成器网络（理论上-实践中，用 REINFORCE 来训练带有离散输出的生成网络非常困难）。大部分其他的框架需要该生成器网络有一些特定的函数形式，比如输出层是高斯的。重要的是所有其他的框架需要生成器网络遍布非零质量（non-zero mass）。
不需要设计遵循任何种类的因式分解的模型，任何生成器网络和任何判别器都会有用。
无需利用马尔科夫链反复采样，无需在学习过程中进行推断（Inference），回避了近似计算棘手的概率的难题。

GAN的缺点：

难以收敛（non-convergence）。目前面临的基本问题是：所有的理论都认为 GAN 应该在纳什均衡（Nash equilibrium）上有卓越的表现，但梯度下降只有在凸函数的情况下才能保证实现纳什均衡。当博弈双方都由神经网络表示时，在没有实际达到均衡的情况下，让它们永远保持对自己策略的调整是可能的【OpenAI Ian Goodfellow的Quora】。
难以训练：崩溃问题（collapse problem）。GAN模型被定义为极小极大问题，没有损失函数，在训练过程中很难区分是否正在取得进展。GAN的学习过程可能发生崩溃问题（collapse problem），生成器开始退化，总是生成同样的样本点，无法继续学习。当生成模型崩溃时，判别模型也会对相似的样本点指向相似的方向，训练无法继续。
无需预先建模，模型过于自由不可控。与其他生成式模型相比，GAN不需要构造分布函数，而是使用一种分布直接进行采样，从而真正达到理论上可以完全逼近真实数据，这也是GAN最大的优势。然而，这种不需要预先建模的方法缺点是太过自由了，对于较大的图片，较多的 pixel的情形，基于简单 GAN 的方式就不太可控了(超高维)。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/269504.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！