目录

力扣62. 不同路径

解析代码

---

力扣62. 不同路径

62. 不同路径

难度 中等

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

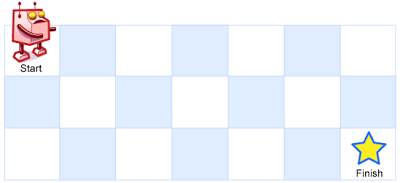
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 10^9

class Solution {
public:int uniquePaths(int m, int n) {}
};

---

解析代码

dp[i][j] 表示：到 [i, j] 位置处，一共有多少种方式。状态转移方程为dp[i][j] = dp[i-1][j] + dp[i][j-1];

class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m+1, vector<int>(n+1, 0)); // 多开一行一列dp[0][1] = 1; // 虚拟结点，保证后面填表正确（让第一行第一列都是1）for(int i = 1; i <= m; ++i){for(int j = 1; j <= n; ++j){dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m][n];}
};