1.景区导游(树上前缀和、最近公共祖先)



思路
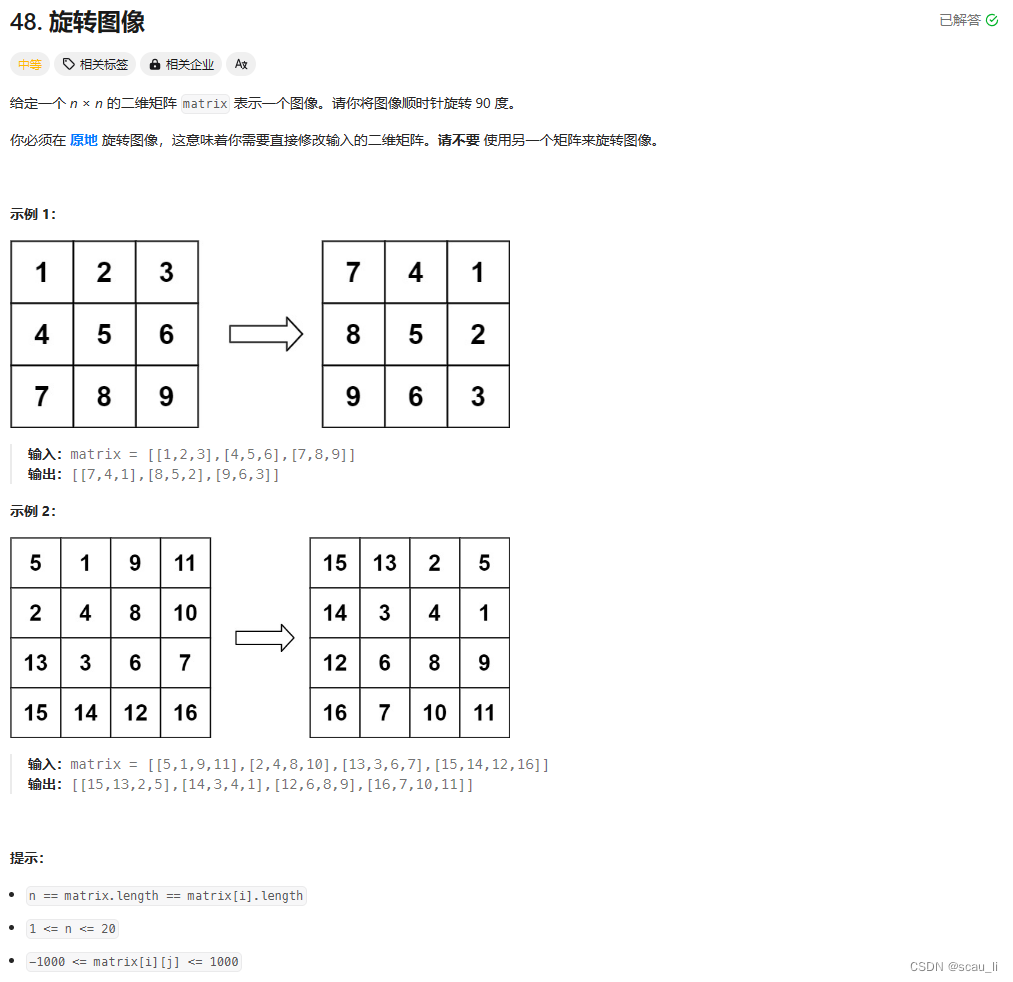
路线:2 -> 6 -> 5 -> 1
1.一个点都不去去掉的花费记作sum
2.去掉第一个点,sum - cost[2 -> 6]
3.去掉第二个点,sum - cost[2 -> 6] - cost[6 -> 5] + cost[2 -> 5]
dfs 中的参数不是一下就想到的,而是在写的过程中,你发现需要某个信息,而这个信息没有被提前记录,所以可以把这个信息当作参数记录下来
正解就是优化 cost 的求法
暴力 dfs(O(k * n))
#include<iostream>
#include<vector>
#include<map>
using namespace std;
const int N = 2e5 + 10;
map<pair<int, int>, int> st; // 存储两个点之间的时间
vector<pair<int, int>> g[N]; // 存储图和时间
int n, k;
int a[N];// 起点、终点、当前节点、父节点、时间总和
bool dfs(int u, int v, int s, int fa, int sum){if(s == v){st[make_pair(u, v)] = sum;st[make_pair(v, u)] = sum;return true;}for(int i = 0; i < g[s].size(); i++){// 子节点int son = g[s][i].first, w = g[s][i].second;// 如果子节点等于父节点,说明重复了跳过if(son == fa) continue;// 父节点为当前节点if(dfs(u, v, son, s, sum + w)) return true;}return false;
}int main(){scanf("%d%d", &n, &k);int u, v, t;for(int i = 0; i < n - 1; i++){scanf("%d%d%d", &u, &v, &t);g[u].push_back(make_pair(v, t));g[v].push_back(make_pair(u, t));}for(int i = 0; i < k; i++) scanf("%d", &a[i]);int ans = 0;for(int i = 1; i < k; i++){dfs(a[i - 1], a[i], a[i - 1], -1, 0);ans += st[make_pair(a[i - 1], a[i])];}for(int i = 0; i < k; i++){int res = ans;if(!i) res -= st[make_pair(a[i], a[i + 1])];else if(i == k - 1) res -= st[make_pair(a[i - 1], a[i])];else{res -= st[make_pair(a[i - 1], a[i])];res -= st[make_pair(a[i], a[i + 1])];dfs(a[i - 1], a[i + 1], a[i - 1], -1, 0);res += st[make_pair(a[i - 1], a[i + 1])];}printf("%d ", res);}return 0;
}
正解(O(n))

#include<iostream>
#include<vector>
using namespace std;
const int N = 2e5 + 10;
typedef long long qq;
vector<pair<int, int>> e[N];
// 存储父节点,存储深度,存储重儿子,存储以当前节点为根的子树节点数,存储当前节点的重链顶点
int fa[N], dep[N], son[N], sz[N], top[N];
qq sum[N]; // 存储树上前缀和
int a[N];
int n, k;// 求出 fa, dep, son, sz
void dfs1(int u, int father){fa[u] = father, dep[u] = dep[father] + 1, sz[u] = 1;for(auto v : e[u]){int s = v.first;if(s == father) continue;dfs1(s, u);sz[u] += sz[s];if(sz[son[u]] < sz[s]) son[u] = s;}
}// 求出 top
void dfs2(int u, int t){// 链头top[u] = t;// 没有重儿子if(!son[u]) return;// 搜重儿子dfs2(son[u], t);for(auto v : e[u]){int s = v.first;if(s == fa[u] || s == son[u]) continue;// 搜轻儿子dfs2(s, s);}
}// 求公共祖先
int lca(int u, int v){while(top[u] != top[v]){if(dep[top[u]] < dep[top[v]]) swap(u, v);u = fa[top[u]];}return dep[u] < dep[v] ? u : v;
}// 求树上前缀和
void cal_sum(int u){for(auto v : e[u]){int s = v.first, w = v.second;if(s == fa[u]) continue;sum[s] = sum[u] + w;cal_sum(s);}
}int main(){scanf("%d%d", &n, &k);int u, v, t;for(int i = 1; i < n; i++){scanf("%d%d%d", &u, &v, &t);e[u].push_back({v, t});e[v].push_back({u, t});}for(int i = 1; i <= k; i++) scanf("%d", &a[i]);dfs1(1, 0);dfs2(1, 1);cal_sum(1);qq ans = 0;for(int i = 2; i <= k; i++){int x = a[i - 1], y = a[i];qq cost = sum[x] + sum[y] - 2 * sum[lca(x, y)];ans += cost;}for(int i = 1; i <= k; i++){qq res = ans;int x = a[i - 1], y = a[i], z = a[i + 1];if(i == 1) res -= sum[y] + sum[z] - 2 * sum[lca(y, z)];else if(i == k) res -= sum[x] + sum[y] - 2 * sum[lca(x, y)];else{res -= sum[x] + sum[y] - 2 * sum[lca(x, y)];res -= sum[y] + sum[z] - 2 * sum[lca(y, z)];res += sum[x] + sum[z] - 2 * sum[lca(x, z)];}printf("%lld ", res);}return 0;
}
2.砍树(树上差分、最近公共祖先)


思路
dfs 找到两个点之间的路径,然后打上标记,如果打上 m 个标记,那么就可以作为答案
正解:优化打标记的过程,边权转换为点权,每个边权为子节点的点权
第一步:给路径的起点和终点都加 1
第二步:给两个点的最近公共祖先减 2
第三步:树上差分
第四步:让每个点都加上他的子树和
点权等于这个点和他父节点相连的边权
暴力 dfs(O(n * m))
#include<iostream>
#include<vector>
#include<map>
using namespace std;
const int N = 2e5 + 10;
map<pair<int, int>, int> id; // 存储编号
vector<int> e[N];
int w[N]; // 存储边权
int n, m;bool dfs(int a, int b, int u, int fa){if(u == b) return true;for(int v : e[u]){if(v == fa) continue;if(dfs(a, b, v, u)){int t = id[{u, v}];w[t]++;return true;}}return false;
}int main()
{scanf("%d%d", &n, &m);int x, y;for(int i = 1; i < n; i++){scanf("%d%d", &x, &y);e[x].push_back(y);e[y].push_back(x);id[{x, y}] = i;id[{y, x}] = i;}int a, b;for(int i = 0; i < m; i++){scanf("%d%d", &a, &b);dfs(a, b, a, -1);}int ans = -1;for(int i = n - 1; i >= 1; i--){if(w[i] == m){ans = i;break;}}printf("%d", ans);return 0;
}
正解(O(n))
#include<iostream>
#include<vector>
#include<map>
using namespace std;
const int N = 2e5 + 10;
int fa[N], dep[N], son[N], sz[N], top[N];
map<pair<int, int>, int> id; // 存储编号
vector<int> e[N];
int w[N]; // 存储点权
int n, m;void dfs1(int u, int father){fa[u] = father, dep[u] = dep[father] + 1, sz[u] = 1;for(int v : e[u]){if(v == father) continue;dfs1(v, u);sz[u] += sz[v];if(sz[son[u]] < sz[v]) son[u] = v;}
}void dfs2(int u, int t){top[u] = t;if(!son[u]) return;dfs2(son[u], t);for(int v : e[u]){if(v == fa[u] || v == son[u]) continue;dfs2(v, v);}
}int lca(int u, int v){while(top[u] != top[v]){if(dep[top[u]] < dep[top[v]]) swap(u, v);u = fa[top[u]];}return dep[u] < dep[v] ? u : v;
}void lca_sum(int u, int father){for(int v : e[u]){if(v == father) continue;lca_sum(v, u);w[u] += w[v];}
}int main()
{scanf("%d%d", &n, &m);int x, y;for(int i = 1; i < n; i++){scanf("%d%d", &x, &y);e[x].push_back(y);e[y].push_back(x);id[{x, y}] = i;id[{y, x}] = i;}dfs1(1, 0);dfs2(1, 1);int a, b;for(int i = 0; i < m; i++){scanf("%d%d", &a, &b);// 树上差分w[a]++, w[b]++;w[lca(a, b)] -= 2;}lca_sum(1, 0);int ans = -1;for(int i = 1; i <= n; i++){if(w[i] == m){int t = id[{i, fa[i]}];ans = max(ans, t);}}printf("%d", ans);return 0;
}
3.三国游戏(贪心)


思路
因为事件是独立的,所以可以从大到小排序,看 a - b - c 的和最多有多少个满足大于0
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N], c[N], d[N];
int n;int f(int a[], int b[], int c[]){for(int i = 1; i <= n; i++) d[i] = a[i] - b[i] - c[i];sort(d + 1, d + n + 1, greater<int>());long long sum = 0;for(int i = 1; i <= n; i++){sum += d[i];if(sum <= 0){sum = i - 1;break;}}return sum > 0 ? sum : -1;
}int main()
{scanf("%d", &n);for(int i = 1; i <= n; i++) scanf("%d", &a[i]);for(int i = 1; i <= n; i++) scanf("%d", &b[i]);for(int i = 1; i <= n; i++) scanf("%d", &c[i]);int res = max(f(a, b, c), max(f(b, a, c), f(c, a, b)));printf("%d", res);return 0;
}
4.填充(贪心)

思路

#include <iostream>
using namespace std;
int main()
{string s;cin>>s;int res = 0;for(int i = 1; i < s.size(); i++){if(s[i - 1] == s[i] || s[i - 1] == '?' || s[i] == '?'){res++;// 成对匹配,如果匹配成功,就跳过后面那个,到后面的后面,再匹配i++;}}cout<<res;return 0;
}
5.翻转(模拟)


思路
如果两边和当前位置相反,且和 t 不同,那就翻转,最后再比较 s 和 t 是否相同
#include <iostream>
using namespace std;
int main()
{int d;cin>>d;string t, s;while(d--){cin>>t>>s;int res = 0;for(int i = 1; i < s.size() - 1; i++){if(s[i] != t[i] && s[i - 1] != s[i] && s[i] != s[i + 1]){s[i] ^= 1;res++;}}if(s == t) cout<<res<<endl;else cout<<-1<<endl;}return 0;
}