数据结构 第2章：线性表

文章目录

  • 2.1 线性表的定义和操作
    • 2.1.1 线性表的基本概念
    • 2.1.2 线性表的基本操作
  • 2.2. 顺序表
    • 2.2.1. 顺序表的基本概念
    • 2.2.2. 顺序表的实现
    • 2.2.3. 顺序表的基本操作
  • 2.3 链表
    • 2.3.1 单链表的基本概念
    • 2.3.2 单链表的实现
    • 2.3.3 单链表的插入
    • 2.3.4. 单链表的删除
    • 2.3.5. 单链表的查找
    • 2.3.6. 单链表的建立
    • 2.3.7. 双链表
    • 2.3.8 循环链表
    • 2.3.9. 静态链表
    • 2.3.10. 顺序表和链表的比较

2.1 线性表的定义和操作

2.1.1 线性表的基本概念

  1. 线性表：是具有相同数据类型的 n 个数据元素的有限序列。

  2. 特点：

存在惟一的第一个元素。
存在惟一的最后一个元素。
除第一个元素之外，每个元素均只有一个直接前驱。
除最后一个元素之外，每个元素均只有一个直接后继。

  1. 线性表的存储结构：
    顺序存储结构：顺序表
    链式存储结构：链表

2.1.2 线性表的基本操作

  1. InitList(&L)：初始化表。构造一个空的线性表 L，并分配内存空间。

  2. DestroyList(&L)：销毁表。并释放线性表 L 占用的内存空间。

  3. ListInsert(&L, i, &e)：插入操作。在表 L 的第 i 个位置插入指定元素 e 。

  4. ListDelete(&L, i, &e)：删除操作。删除表 L 中第 i 个位置的元素，并用 e 返回删除元素的值。

  5. LocateElem(L, e)：按值查找。在表 L 中查找具有给定元素值的元素。

  6. GetElem(L, i)：按位查找。获取表 L 中第 i 个位置的元素的值。

  7. Length(L)：求表长。返回线性表 L 的长度，即表中元素的个数。

  8. PrintList(L)：打印表。按顺序输出线性表 L 的所有元素值。

  9. Empty(L)：判断是否为空。若 线性表L 为空表，则返回 true，否则返回 false。

操作数据结构的思路：创销、增删改查

2.2. 顺序表

2.2.1. 顺序表的基本概念

  1. 顺序表：用顺序存储的方式实现线性表。顺序存储，将逻辑上相邻的元素存储在相邻的物理位置上。
  2. 特点：
  1. 随机访问，即可以在 O ( 1 )时间内找到第 i 个元素。
  2. 存储密度高，每个节点只存储数据元素。
  3. 拓展容量不方便（即使使用动态分配的方式实现，拓展长度的时间复杂度也比较高，因为需要把数据复制到新的区域）。
  4. 插入删除操作不方便，需移动大量元素：O ( n )

2.2.2. 顺序表的实现

静态实现：

#define MaxSize 10 // 定义最大长度 typedef struct {int data[MaxSize]; // 使用静态的数组存放数据元素 int length; // 顺序表的当前长度 
}SqList;// 初始化顺序表 
void InitList(SqList &L) {L.length = 0; // 顺序表初始长度为0 
}int main() {SqList L; // 声明一个顺序表 InitList(L); // 初始化顺序表 return 0;
}

动态实现：

#define InitSize 10 // 顺序表的初始长度typedef struct {int *data; // 声明动态分配数组的指针 int MaxSize; // 顺序表的最大容量int length; // 顺序表的当前长度 
}SeqList;// 初始化顺序表 
void InitList(SqList &L) {// 用malloc函数申请一片连续的存储空间 L.data = (int *)malloc(InitSize * sizeof(int));L.length = 0;L.MaxSize = InitSize;
}// 增加动态数组的长度 
void IncreaseSize(SqList &L, int len) {int *p = L.data;L.data = (int *)malloc((L.MaxSize+len) * sizeof(int));for (int i = 0; i < L.length; i++)L.data[i] = p[i]; // 将数据复制到新区域 L.MaxSize = L.MaxSize + len; // 顺序表最大长度增加len free(p); // 释放原来的内存空间 
}int main() {SeqList L; // 声明一个顺序表 InitList(L); // 初始化顺序表 ...IncreaseSize(L, 5);return 0;
}

malloc() 函数的作用：会申请一片存储空间，并返回存储空间第一个位置的地址，也就是该位置的指针。

2.2.3. 顺序表的基本操作

  1. 插入：
#define MaxSize 10 // 定义最大长度 typedef struct {int data[MaxSize]; // 用静态的数组存放数据元素 int length; // 顺序表的当前长度 
}SqList;// 在顺序表i位置插入e
bool ListInsert(SqList &L, int i, int e) {if (i < 1 || i > L.length+1) // 判断i的范围是否有效 return false;if (L.length >= MaxSize) // 判断存储空间是否已满 return false;for (int j = L.length; j >= i; j--) // 将第i个元素之后的元素后移 L.data[j] = L.data[j-1];L.data[i-1] = e; // 在位置i处放入e L.length++; // 长度+1 return true;
} int main() {SqList L;InitList(L);ListInsert(L, 3, 3);return 0; 
}

时间复杂度：

  1. 最好时间复杂度：O ( 1 )
  2. 最坏时间复杂度：O ( n )
  3. 平均时间复杂度：O ( n )
  1. 删除：
#define MaxSize 10typedef struct {int data[MaxSize];int length;
} SqList;// 删除顺序表i位置的数据并存入e
bool ListDelete(SqList &L, int i, int &e) {if (i < 1 || i > L.length) // 判断i的范围是否有效return false;e = L.data[i-1]; // 将被删除的元素赋值给e for (int j = i; j < L.length; j++) //将第i个位置后的元素前移 L.data[j-1] = L.data[j];L.length--;return true; 
}int main() {SqList L;InitList(L);int e = -1;if (ListDelete(L, 3, e))printf("已删除第3个元素，删除元素值为%d\n", e);elseprintf("位序i不合法，删除失败\n"); return 0; 
}

时间复杂度：

  1. 最好时间复杂度：O ( 1 )
  2. 最坏时间复杂度：O ( n )
  3. 平均时间复杂度：O ( n )
  1. 按位查找：
// 静态分配的按位查找
#define MaxSize 10typedef struct {ElemType data[MaxSize]; int length;
}SqList;ElemType GetElem(SqList L, int i) {return L.data[i-1];
}

// 动态分配的按位查找
#define InitSize 10typedef struct {ElemType *data;int MaxSize;int length;
}SeqList;ElemType GetElem(SeqList L, int i) {return L.data[i-1];
}

时间复杂度： O ( 1 )

  1. 按值查找：
#define InitSize 10typedef struct {ElemType *data; int MaxSize;int length; 
}SqList;// 查找第一个元素值为e的元素，并返回其位序 
int LocateElem(SqList L, ElemType e) {for (int i = 0; i < L.length; i++)if (L.data[i] == e)return i+1; // 数组下标为i的元素值等于e，返回其位序i+1 return 0; // 没有查找到 
}

在《数据结构》考研初试中，手写代码可以直接用“==”，无论 ElemType 是基本数据类型还是结构类型
时间复杂度：

  1. 最好时间复杂度：O ( 1 ) O(1)O(1)
  2. 最坏时间复杂度：O ( n ) O(n)O(n)
  3. 平均时间复杂度：O ( n ) O(n)O(n)

2.3 链表

2.3.1 单链表的基本概念

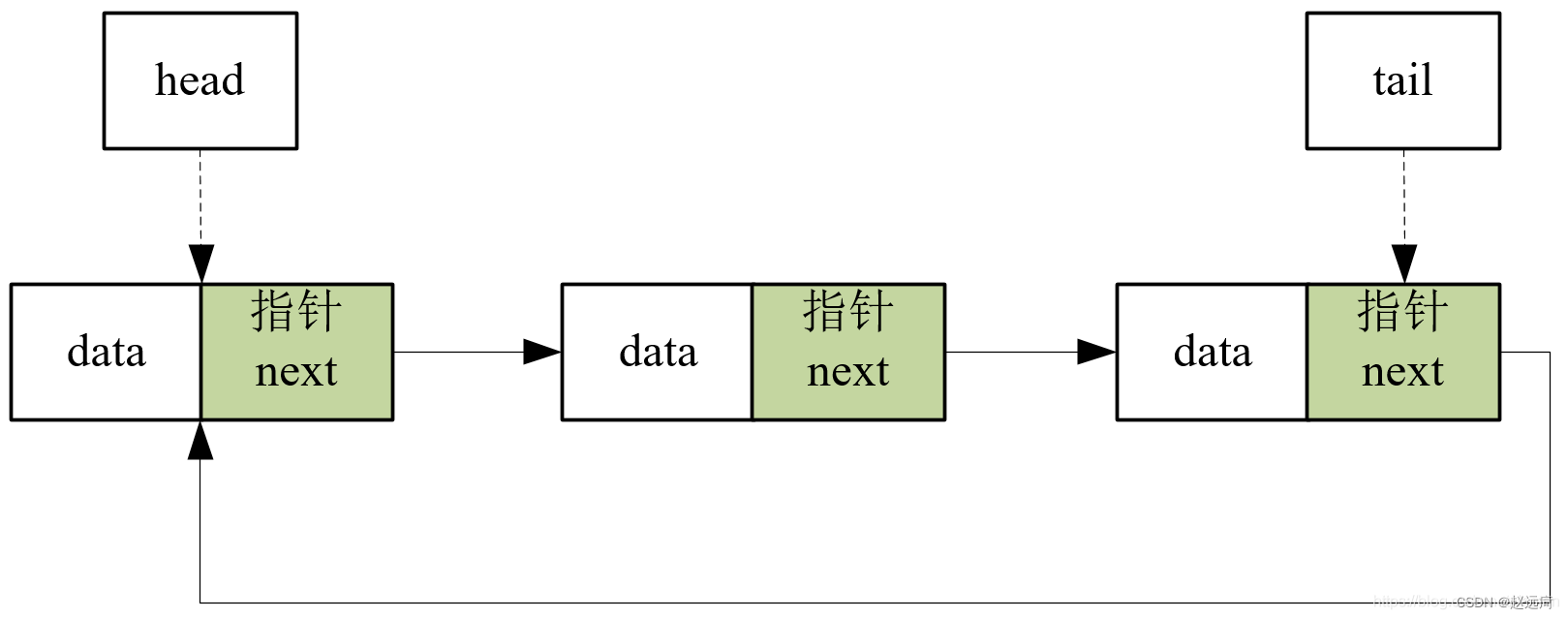
在这里插入图片描述

  1. 单链表：用链式存储实现了线性结构。一个结点存储一个数据元素，各结点间的前后关系用一个指针表示。
  2. 特点：
    优点：不要求大片连续空间，改变容量方便。
    缺点：不可随机存取，要耗费一定空间存放指针。
  3. 两种实现方式：
    带头结点，写代码更方便。头结点不存储数据，头结点指向的下一个结点才存放实际数据。
    不带头结点，麻烦。对第一个数据结点与后续数据结点的处理需要用不同的代码逻辑，对空表和非空表的处理需要用不同的代码逻辑。

2.3.2 单链表的实现

不带头结点的单链表：

typedef struct LNode{ElemType data;struct LNode *next;
}LNode, *LinkList;//初始化一个空的单链表
bool InitList(LinkList &L){L = NULL; //空表，暂时还没有任何结点return true;
}void test(){LinkList L;  //声明一个指向单链表的头指针//初始化一个空表InitList(L);...
}//判断单链表是否为空
bool Empty(LinkList L){return (L==NULL)
}

带头结点的单链表：

typedef struct LNode{      ElemType data;      struct LNode *next;
}LNode, *LinkList;// 初始化一个单链表（带头结点）
bool InitList(LinkList &L){      L = (LNode *)malloc(sizeof(LNode));  //分配一个头结点 if (L == NULL)        //内存不足，分配失败    return false;    L->next = NULL;       //头结点之后暂时还没有结点   return true;
}void test(){     LinkList L;  //声明一个指向单链表的头指针 //初始化一个空表    InitList(L);     ...
}
//判断单链表是否为空
bool Empty(LinkList L){  if (L->next == NULL) return true;     else             return false;
}

2.3.3 单链表的插入

  1. 按位序插入（带头结点）：
typedef struct LNode{     ElemType data;  struct LNode *next;
}LNode, *LinkList;//在第i个位置插入元素e
bool ListInsert(LinkList &L, int i, ElemType e){       if(i<1)         return False;   LNode *p;           //指针p指向当前扫描到的结点    int j=0;            //当前p指向的是第几个结点   p = L;              //循环找到第i-1个结点    while(p!=NULL && j<i-1){       //如果i>lengh，p最后会等于NULL p = p->next;              j++;      }       //p值为NULL说明i值不合法   if (p==NULL)            return false;       //在第i-1个结点后插入新结点  LNode *s = (LNode *)malloc(sizeof(LNode)); s->data = e;     s->next = p->next; p->next = s;       //将结点s连到p后      return true;
}

时间复杂度：

  1. 最好时间复杂度：O ( 1 )
  2. 最坏时间复杂度：O ( n )
  3. 平均时间复杂度：O ( n )
  1. 按位序插入（不带头结点）：
typedef struct LNode{     ElemType data;      struct LNode *next;
}LNode, *LinkList;//在第i个位置插入元素e
bool ListInsert(LinkList &L, int i, ElemType e){   //判断i的合法性     if(i<1)      return false; //需要判断插入的位置是否是第1个     if(i==1){              LNode *s = (LNode *)malloc(size of(LNode));  s->data =e;          s->next =L;       L=s;          //头指针指向新结点   return true;      }       //i>1的情况与带头结点一样，唯一区别是j的初始值为1   LNode *p;       //指针p指向当前扫描到的结点     int j=1;        //当前p指向的是第几个结点   p = L;          //循环找到第i-1个结点    while(p!=NULL && j<i-1){     //如果i>lengh，p最后会等于NULL    p = p->next;             j++;      }       //p值为NULL说明i值不合法   if (p==NULL)           return false;      //在第i-1个结点后插入新结点   LNode *s = (LNode *)malloc(sizeof(LNode));  s->data = e;      s->next = p->next;  p->next = s;        return true;
}

时间复杂度：

  1. 最好时间复杂度：O ( 1 )
  2. 最坏时间复杂度：O ( n )
  3. 平均时间复杂度：O ( n )

除非特别声明，否则之后的代码都默认为带头结点！
3. 指定结点的后插操作：

typedef struct LNode{        ElemType data;        struct LNode *next;
}LNode, *LinkList;// 在结点p后插入元素e
bool InsertNextNode(LNode *p, ElemType e){      if(p==NULL){         return false;   }    LNode *s = (LNode *)malloc(sizeof(LNode));     if(s==NULL)     return false;    s->data = e;     s->next = p->next;  p->next = s;     return true;
}// 按位序插入的函数中可以直接调用后插操作
bool ListInsert(LinkList &L, int i, ElemType e){  if(i<1)            return False;LNode *p;     //指针p指向当前扫描到的结点 int j=0;        //当前p指向的是第几个结点 p = L;       //循环找到第i-1个结点   while(p!=NULL && j<i-1){ //如果i>lengh, p最后会等于NULL   p = p->next;        j++;       }       return InsertNextNode(p, e)
}

时间复杂度：O ( 1 )

  1. 指定结点的前插操作：

如果传入头指针，就可以循环整个链表找到指定结点p的前驱结点q，再对q进行后插操作；
如果不传入头指针，可以在指定结点p后插入一个结点s，并交换两个结点所保存的数据，从而变相实现指定结点的前插操作。

typedef struct LNode{     ElemType data;      struct LNode *next;
}LNode, *LinkList;// 在结点p前插入元素e
bool InsertPriorNode(LNode *p, ElemType e){  if(p==NULL)      return false;  LNode *s = (LNode *)malloc(sizeof(LNode));  // 内存不足分配失败       if(s==NULL)       return false;    // 将s插入结点p之后    s->next = p->next;   p->next = s;       // 交换两个结点中的数据  s->data = p->data;   p->data = e;       return true;
}

时间复杂度：O ( 1 )

2.3.4. 单链表的删除

  1. 按位序删除：
typedef struct LNode{       ElemType data;    struct LNode *next;}LNode, *LinkList;// 删除第i个结点并将其所保存的数据存入e
bool ListDelete(LinkList &L, int i, ElemType &e){      if(i<1)             return false;     LNode *p;       //指针p指向当前扫描到的结点     int j=0;        //当前p指向的是第几个结点    p = L;         //循环找到第i-1个结点     while(p!=NULL && j<i-1){   //如果i>lengh，p和p的后继结点会等于NULL        p = p->next;            j++;      }       if(p==NULL)       return false;    if(p->next == NULL)        return false;    	   //令q暂时保存被删除的结点   LNode *q = p->next;    e = q->data;     p->next = q->next;      free(q)     return true;
}

时间复杂度：
最好时间复杂度：O ( 1 )
最坏时间复杂度：O ( n )
平均时间复杂度：O ( n )

  1. 删除指定结点：
  1. 如果传入头指针，就可以循环整个链表找到指定结点p的前驱结点q，再对p进行删除操作；
  2. 如果不传入头指针，可以把指定结点p的后继结点q删除，并使结点p保存结点q存储的数据，从而变相实现删除指定结点的操作。但是如果指定结点p没有后继结点，这么做会报错。
// 删除指定结点p
bool DeleteNode(LNode *p){   if(p==NULL)           return false;     LNode *q = p->next; // 令q指向p的后继结点  // 如果p是最后一个结点，则q指向NULL，继续执行就会报错  p->data = q->data;  p->next = q->next;   free(q);    return true;
}

时间复杂度：O ( 1 )

2.3.5. 单链表的查找

  1. 按位查找：
typedef struct LNode{  ElemType data;    struct LNode *next;
}LNode, *LinkList;// 查找指定位序i的结点并返回
LNode * GetElem(LinkList L, int i){   if(i<0)            return NULL;   LNode *p;     int j=0;     p = L;      while(p!=NULL && j<i){   p = p->next;     j++;      }        return p;
}// 封装后的插入操作，在第i个位置插入元素e，可以调用查询操作和后插操作
bool ListInsert(LinkList &L, int i, ElemType e){  if(i<1)             return False;  // 找到第i-1个元素     LNode *p = GetElem(L, i-1);   // 在p结点后插入元素e     return InsertNextNode(p, e)
}

时间复杂度：
最好时间复杂度：O ( 1 )
最坏时间复杂度：O ( n )
平均时间复杂度：O ( n )

  1. 按值查找：
// 查找数据域为e的结点指针，否则返回NULL
LNode * LocateElem(LinkList L, ElemType e){           LNode *P = L->next;     // 从第一个结点开始查找数据域为e的结点  while(p!=NULL && p->data != e){   p = p->next;     }     return p;
}

时间复杂度：
最好时间复杂度：O ( 1 )
最坏时间复杂度：O ( n )
平均时间复杂度：O ( n )

  1. 计算单链表长度：
// 计算单链表的长度
int Length(LinkList L){      int len=0;       //统计表长  LNode *p = L;while(p->next != NULL){ p = p->next;      len++;       }      return len;
}

时间复杂度：O ( n )

2.3.6. 单链表的建立

  1. 尾插法建立单链表：
// 使用尾插法建立单链表L
LinkList List_TailInsert(LinkList &L){   int x;			//设ElemType为整型int  L = (LinkList)malloc(sizeof(LNode));     //建立头结点(初始化空表)     LNode *s, *r = L;                        //r为表尾指针    scanf("%d", &x);                         //输入要插入的结点的值   while(x!=9999){                          //输入9999表示结束     s = (LNode *)malloc(sizeof(LNode));    s->data = x;           r->next = s;           r = s;                               //r指针指向新的表尾结点     scanf("%d", &x);       }    r->next = NULL;                          //尾结点指针置空      return L;
}

时间复杂度：O（n）

  1. 头插法建立单链表：
LinkList List_HeadInsert(LinkList &L){       //逆向建立单链表   LNode *s;      int x;     L = (LinkList)malloc(sizeof(LNode));     //建立头结点   L->next = NULL;                          //初始为空链表,这步很关键  scanf("%d", &x);                         //输入要插入的结点的值  while(x!=9999){                          //输入9999表结束     s = (LNode *)malloc(sizeof(LNode)); s->data = x;          s->next = L->next;      L->next = s;          //将新结点插入表中，L为头指针   scanf("%d", &x);       }     return L;
}

头插法实现链表的逆置：

// 将链表L中的数据逆置并返回
LNode *Inverse(LNode *L){	LNode *p, *q;	  p = L->next;     //p指针指向第一个结点	  L->next = NULL;  //头结点置空       // 依次判断p结点中的数据并采用头插法插到L链表中	while (p != NULL){		   q = p;		  p = p->next;	q->next = L->next;  L->next = q;	}	   return L;
}

2.3.7. 双链表

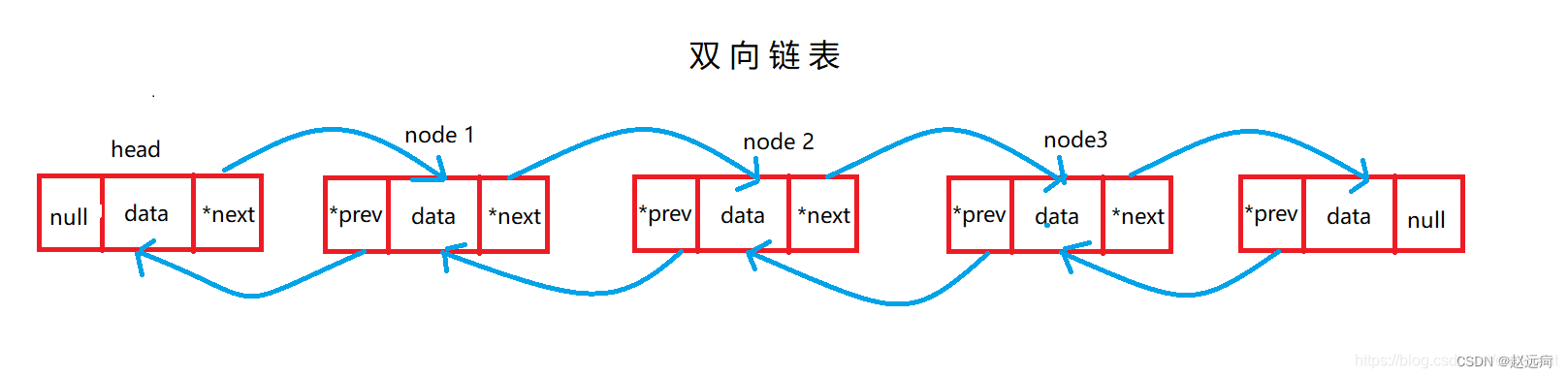
在这里插入图片描述

  1. 双链表的定义：双链表也是链表的一种。双链表的每个数据节点中都有两个指针，分别指向前驱节点和后继结点。
  2. 双链表的实现：
typedef struct DNode{            //定义双链表结点类型 ElemType data;               //数据域    struct DNode *prior, *next;  //前驱和后继指针
}DNode, *DLinklist;
  1. 双链表的初始化 (带头结点)：
typedef struct DNode{   ElemType data;     struct DNode *prior, *next;
}DNode, *DLinklist;// 初始化双链表
bool InitDLinkList(Dlinklist &L){     L = (DNode *)malloc(sizeof(DNode)); if(L==NULL)            return false;    L->prior = NULL;   //头结点的prior指针永远指向NULL     L->next = NULL;    //头结点之后暂时还没有结点，置空   return true;
}void testDLinkList(){  DLinklist L;       InitDLinkList(L);       ...
}// 判断双链表是否为空
bool Empty(DLinklist L){   if(L->next == NULL)   return true;      else             return false;
}
  1. 双链表的后插操作：
typedef struct DNode{     ElemType data;       struct DNode *prior, *next;
}DNode, *DLinklist;// 将结点s插入到结点p之后
bool InsertNextDNode(DNode *p, DNode *s){ if(p==NULL || s==NULL)  return false;         s->next = p->next;      // 判断结点p之后是否有后继结点  if (p->next != NULL)   p->next->prior = s; s->prior = p;   p->next = s;     return true;
}

双链表的前插操作、按位序插入操作都可以转换成后插操作

  1. 双链表的删除操作：
// 删除p结点的后继结点
bool DeletNextDNode(DNode *p){   if(p==NULL)           return false;   // 找到p的后继结点q    DNode *q =p->next;   if(q==NULL)          return false;    p->next = q->next;   if(q->next != NULL) q->next->prior=p;  free(q);     return true;
}// 销毁一个双链表
bool DestoryList(DLinklist &L){ // 循环释放各个数据结点   while(L->next != NULL){    DeletNextDNode(L);      free(L);        // 头指针置空  L=NULL;     }
}
  1. 双链表的遍历：
// 删除p结点的后继结点
bool DeletNextDNode(DNode *p){   if(p==NULL)           return false;   // 找到p的后继结点q    DNode *q =p->next;   if(q==NULL)          return false;    p->next = q->next;   if(q->next != NULL) q->next->prior=p;  free(q);     return true;
}// 销毁一个双链表
bool DestoryList(DLinklist &L){ // 循环释放各个数据结点   while(L->next != NULL){    DeletNextDNode(L);      free(L);        // 头指针置空  L=NULL;     }
}

双链表不可随机存取，按位查找、按值查找操作都只能用遍历的方式实现。

2.3.8 循环链表

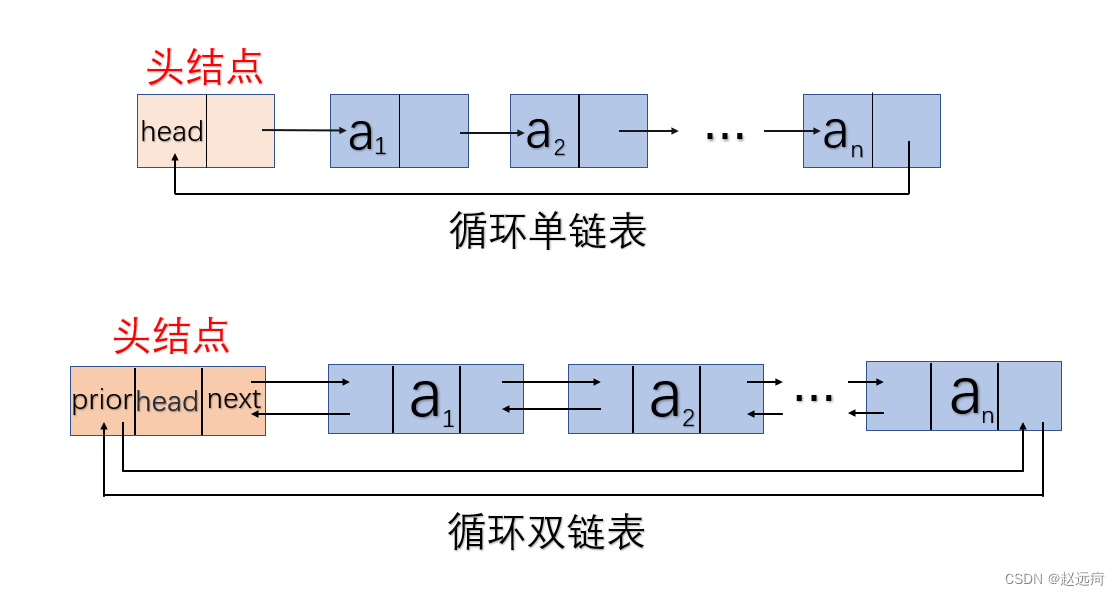
在这里插入图片描述

  1. 循环链表的定义： 循环链表是另一种形式的链式存储结构。它的特点是表中最后一个结点的指针域指向头结点，整个链表形成一个环。
  2. 循环单链表的实现：
typedef struct LNode{           ElemType data;                  struct LNode *next; 
}DNode, *Linklist;// 初始化循环单链表
bool InitList(LinkList &L){    L = (LNode *)malloc(sizeof(LNode));  if(L==NULL)             return false;    // 最后一个结点的next指针指向头结点    L->next = L;       return true;
}// 判断循环单链表是否为空
bool Empty(LinkList L){    if(L->next == L)       return true;    else             return false;
}// 判断结点p是否为循环单链表的表尾结点
bool isTail(LinkList L, LNode *p){ if(p->next == L)          return true;      else            return false;
}
  1. 循环双链表的实现：
typedef struct DNode{            ElemType data;           struct DNode *prior, *next;  
}DNode, *DLinklist;// 初始循环双链表
bool InitDLinkList(DLinklist &L){  L = (DNode *) malloc(sizeof(DNode));  if(L==NULL)            return false;    // 头结点的prior指针指向最后一个结点，最后一个结点的next指针指向头结点 L->prior = L;      L->next = L;
}// 判断循环双链表是否为空
bool Empty(DLinklist L){   if(L->next == L)       return true;      else           return false;
}// 判断结点p是否为循环双链表的表尾结点
bool isTail(DLinklist L, DNode *p){   if(p->next == L)        return true;     else            return false;
}
  1. 循环双链表的插入和删除操作：
// 将结点s插入到结点p之后
bool InsertNextDNode(DNode *p, DNode *s){  s->next = p->next;   //循环双链表不用担心p结点的下一个结点为空   p->next->prior = s;  s->prior = p;     p->next = s;
}// 删除p结点的后继结点
bool DeletNextDNode(DNode *p){  // 找到p的后继结点q       DNode *q =p->next;        //循环双链表不用担心q结点的下一个结点为空  p->next = q->next;    q->next->prior=p;    free(q);      return true;
}

2.3.9. 静态链表

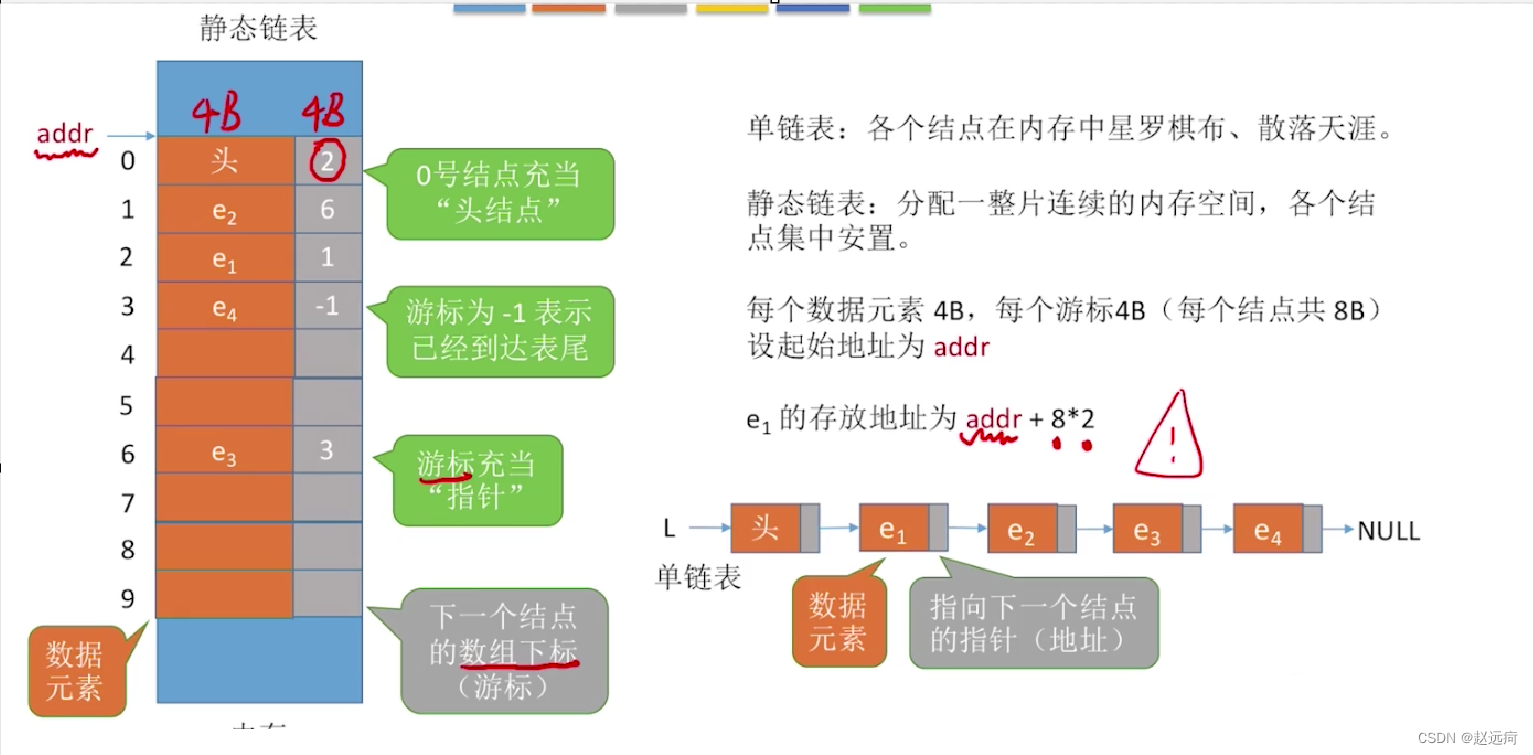
  1. 静态链表的定义：用数组的方式实现的链表。分配一整片连续的内存空间，各个结点集中安置，每个结点包括了数据元素和下一个结点的数组下标。
    在这里插入图片描述

  2. 特点：

    • 优点：增、删操作不需要大量移动元素。
    • 缺点：不能随机存取，只能从头结点开始依次往后查找，容量固定不变！

  3. 静态链表的定义：

#define MaxSize 10        //静态链表的最大长度
struct Node{              //静态链表结构类型的定义  ElemType data;        //存储数据元素    int next;             //下一个元素的数组下标
};// 用数组定义多个连续存放的结点
void testSLinkList(){    struct Node a[MaxSize];  //数组a作为静态链表, 每一个数组元素的类型都是struct Node    ...
}

也可以这么定义：

#define MaxSize 10        //静态链表的最大长度
typedef struct{           //静态链表结构类型的定义       ELemType data;        //存储数据元素     int next;             //下一个元素的数组下标
}SLinkList[MaxSize];void testSLinkList(){      SLinkList a;
}

第一种是我们更加熟悉的写法，第二种写法则更加侧重于强调 a 是一个静态链表而非数组。

  1. 静态链表的注意点：

    • 初始化静态链表时，需要把a[0]的next设为-1，并将空闲结点的next设置为某个特殊值，比如-2。
    • 按位序查找结点时，从头结点出发挨个往后遍历结点，时间复杂度 O = ( n ) O=(n)O=(n)。
    • 按位序插入结点的步骤：①找到一个空的结点，存入数据元素；②从头结点出发找到位序为 i-1 的结点；③修 改新结点的next 为 -1；④修改 i-1 号结点的next为新结点的下标；

2.3.10. 顺序表和链表的比较

  1. 逻辑结构：顺序表和链表都属于线性表，都是线性结构。

  2. 存储结构：

    • 顺序表：顺序存储
      优点：支持随机存取，存储密度高。
      缺点：大片连续空间分配不方便，改变容量不方便。

    • 链表：链式存储
      优点：离散的小空间分配方便，改变容量方便。
      缺点：不可随机存取，存储密度低。

  3. 基本操作 - 创建：

    • 顺序表：需要预分配大片连续空间。若分配空间过小，则之后不方便拓展容量；若分配空间过大，则浪费内存资源。
      • 静态分配：静态数组，容量不可改变。
      • 动态分配：动态数组，容量可以改变，但是需要移动大量元素，时间代价高（使用malloc()、free()）。
    • 链表：只需要分配一个头结点或者只声明一个头指针。

  4. 基本操作 - 销毁：

    • 顺序表：修改 Length = 0
      静态分配：静态数组——系统自动回收空间。
      动态分配：动态数组——需要手动free()。
    • 链表：依次删除各个结点 free()。

  5. 基本操作 - 增/删：

    • 顺序表：插入 / 删除元素要将后续元素后移 / 前移；时间复杂度：O ( n ) O(n)O(n)，时间开销主要来自于移动元素。
    • 链表：插入 / 删除元素只需要修改指针；时间复杂度：O ( n ) O(n)O(n)，时间开销主要来自查找目标元素。

  6. 基本操作 - 查找：

    • 顺序表
      • 按位查找：O ( 1 ) O(1)O(1)
      • 按值查找：O ( n ) O(n)O(n)，若表内元素有序，可在 O ( l o g 2 n ) O(log2n)O(log2n) 时间内找到（二分法）
    • 链表：
      • 按位查找：O ( n ) O(n)O(n)
      • 按值查找：O ( n ) O(n)O(n)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/274529.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

软考69-上午题-【面向对象技术2-UML】-关系

软考69-上午题-【面向对象技术2-UML】-关系

一、关系 UML中有4种关系&#xff1a; 依赖&#xff1b;关联&#xff1b;泛化&#xff1b;实现。 依赖&#xff1a;两个事物之间的语义关系&#xff1b;其中一个事物发生变化会影响另一个事物的语义。 关联&#xff1a;一组对象之间连接的结构关系。 泛化&#xff1a;一般/特…
阅读更多...
【libwebrtc】基于m114的构建

【libwebrtc】基于m114的构建

libwebrtc A C++ wrapper for binary release, mainly used for flutter-webrtc desktop (windows, linux, embedded).是 基于m114版本的webrtc 最新（20240309 ） 的是m122了。官方给出的构建过程 .gclient 文件 solutions = [{"name" : src,"url
阅读更多...
一篇论文回顾 Sora 文生视频技术的背景、技术和应用。

一篇论文回顾 Sora 文生视频技术的背景、技术和应用。

一篇论文回顾 Sora 文生视频技术的背景、技术和应用。 追赶 Sora&#xff0c;成为了很多科技公司当下阶段的新目标。研究者们好奇的是&#xff1a;Sora 是如何被 OpenAI 发掘出来的&#xff1f;未来又有哪些演进和应用方向&#xff1f; Sora 的技术报告披露了一些技术细节&…
阅读更多...
docker部署springboot jar包项目

docker部署springboot jar包项目

docker部署springboot jar包项目 前提&#xff0c;服务器环境是docker环境&#xff0c;如果服务器没有安装docker&#xff0c;可以先安装docker环境。 各个环境安装docker&#xff1a; Ubuntu上安装Docker&#xff1a; ubuntu离线安装docker: CentOS7离线安装Docker&#xff1…
阅读更多...
04-微服务 面试题

04-微服务 面试题

目录 1.Spring Cloud 常见的组件有哪些？ 2.服务注册和发现是什么意思？（Spring Cloud 如何实现服务注册发现） 3.你们项目负载均衡如何实现的 ? 4.什么是服务雪崩，怎么解决这个问题？ 5.你们服务是怎么监控的？ 6.微服务限流（漏桶算法、令牌桶算法） 7.解释一下CAP…
阅读更多...
【AI绘画】免费GPU Tesla A100 32G算力部署Stable Diffusion

【AI绘画】免费GPU Tesla A100 32G算力部署Stable Diffusion

免责声明 在阅读和实践本文提供的内容之前&#xff0c;请注意以下免责声明&#xff1a; 侵权问题: 本文提供的信息仅供学习参考&#xff0c;不用做任何商业用途&#xff0c;如造成侵权&#xff0c;请私信我&#xff0c;我会立即删除&#xff0c;作者不对读者因使用本文所述方法…
阅读更多...
【死磕Elasticsearch】从实战中来，到实战中去

【死磕Elasticsearch】从实战中来，到实战中去

文章目录 写在前面&#xff1a;1、索引阻塞的种类2、什么时候使用阻塞&#xff1f;场景1&#xff1a;进行系统维护场景。场景2&#xff1a;保护数据不被随意更改场景。场景3&#xff1a;优化资源使用的场景。场景4&#xff1a;遵守安全规则场景。 3、添加索引阻塞API4、解除设置…
阅读更多...
QGIS 开发之旅一《二次开发环境搭建》

QGIS 开发之旅一《二次开发环境搭建》

1、 安装QT 下载QT Index of /new_archive/qt 我选择的版本是 Qt5.14.2 2、安装VS2017 Downloads & Keys - Visual Studio Subscriptions。下载后选择windows通用平台开发和C 开发就可以了。 3、安装插件QT vs tools 搜索 qt vs tools&#xff0c;选择第一个安装 …
阅读更多...
安卓简单登录

安卓简单登录

注意 有的朋友不知道登录咋写&#xff0c;这里我就简单给出相应代码&#xff0c;用的本地存储&#xff0c;没用网络请求&#xff0c;有需要可以替换成想要的&#xff0c;废话不多上代码 登录 import androidx.appcompat.app.AppCompatActivity;import android.content.Context…
阅读更多...
springboot的Converter和HttpMessageConveter

springboot的Converter和HttpMessageConveter

Converter和HttpMessageConveter是springboot和springmvc在处理请求的时候需要用到的。但是这两者的完全是不一样的&#xff0c;作用的地方也不一样。 1&#xff0c;springboot和springmvc处理请求的流程 先来回顾一下处理请求的流程&#xff1a; 用户向服务器发送请求&#…
阅读更多...
WebSocket：实现客户端与服务器实时通信的技术

WebSocket：实现客户端与服务器实时通信的技术

&#x1f90d; 前端开发工程师、技术日更博主、已过CET6 &#x1f368; 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 &#x1f560; 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 &#x1f35a; 蓝桥云课签约作者、上架课程《Vue.js 和 E…
阅读更多...
嵌入式系统工程师错题总结

嵌入式系统工程师错题总结

笔者来介绍一下嵌入式系统工程师考试的一些易错题目 题目介绍  流水线指令计算公式&#xff1a;一条指令总时间max&#xff08;单个指令执行时间&#xff09;*&#xff08;指令数-1&#xff09;  平均故障间隔时间  ICMP协议&#xff1a;传送通信问题相关的消息。 …
阅读更多...
12双体系Java学习之局部变量和作用域

12双体系Java学习之局部变量和作用域

局部变量 局部变量的作用域 参数变量
阅读更多...
小白必看，靠这几步写一份简单的产品说明书！

小白必看，靠这几步写一份简单的产品说明书！

我们都知道&#xff0c;无论是新产品发布&#xff0c;还是老产品的推广&#xff0c;产品说明书都扮演着至关重要的角色。产品说明书可以帮助用户正确、高效地使用产品&#xff0c;也是传递企业发展理念、展示企业形象的有效途径。但作为一个小白&#xff0c;怎样才能写一份简单…
阅读更多...
Python 导入Excel三维坐标数据 生成三维曲面地形图(面) 4-1、线条平滑曲面(原始图形)

Python 导入Excel三维坐标数据 生成三维曲面地形图(面) 4-1、线条平滑曲面(原始图形)

环境和包: 环境 python:python-3.12.0-amd64包: matplotlib 3.8.2 pandas 2.1.4 openpyxl 3.1.2 scipy 1.12.0 代码: import pandas as pd import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from scipy.interpolate import griddata fro…
阅读更多...
【Vue+ElementUI】Table表格实现自定义表头展示+表头拖拽排序（附源码）

【Vue+ElementUI】Table表格实现自定义表头展示+表头拖拽排序（附源码）

效果图 因项目采用的是Vue2&#xff0c;所以这个功能目前采用的是Vue2的写法。 Vue3请自行修改扩展代码&#xff1b;或收藏关注帖子&#xff0c;后续Vue3项目如有用到会在本帖子更新修改。 安装vuedraggable&#xff08;拖拽插件&#xff09; cnpm i vuedraggable先说用法&…
阅读更多...
prometheus 原理（架构，promql表达式，描点原理）

prometheus 原理（架构，promql表达式，描点原理）

大家好&#xff0c;我是蓝胖子&#xff0c;提到监控指标&#xff0c;不得不说prometheus&#xff0c;今天这篇文章我会对prometheus 的架构设计&#xff0c;promql表达式原理和监控图表的绘图原理进行详细的解释。来让大家对prometheus的理解更加深刻。 架构设计 先来看看&am…
阅读更多...
【REST2SQL】12 REST2SQL增加Token生成和验证

【REST2SQL】12 REST2SQL增加Token生成和验证

【REST2SQL】01RDB关系型数据库REST初设计 【REST2SQL】02 GO连接Oracle数据库 【REST2SQL】03 GO读取JSON文件 【REST2SQL】04 REST2SQL第一版Oracle版实现 【REST2SQL】05 GO 操作 达梦 数据库 【REST2SQL】06 GO 跨包接口重构代码 【REST2SQL】07 GO 操作 Mysql 数据库 【RE…
阅读更多...
【Echarts】曲线图上方显示数字以及自定义值，标题和副标题居中，鼠标上显示信息以及自定义信息

【Echarts】曲线图上方显示数字以及自定义值，标题和副标题居中，鼠标上显示信息以及自定义信息

欢迎来到《小5讲堂》 大家好&#xff0c;我是全栈小5。 这是《前端》系列文章&#xff0c;每篇文章将以博主理解的角度展开讲解&#xff0c; 特别是针对知识点的概念进行叙说&#xff0c;大部分文章将会对这些概念进行实际例子验证&#xff0c;以此达到加深对知识点的理解和掌握…
阅读更多...
个人博客系列-后端项目-RBAC角色管理（6）

个人博客系列-后端项目-RBAC角色管理（6）

修改上一篇文章创建的用户表 ## 用户表 from django.contrib.auth.hashers import make_password, check_password from django.contrib.auth.models import AbstractBaseUserclass User(AbstractBaseUser):username models.CharField(max_length255, uniqueTrue, verbose_na…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023