双环PID控制详细讲解

参考博客：
（1）PID双环控制（速度环和位置环）
（2）PID控制（四）（单环与双环PID）
（3）内外双环pid算法

0 单环PID

目标位置→系统→速度→当前位置
输入目标位置，得到输出的位置是当前位置作为反馈量，而这个输出结果的位置量是我们通过控制中间过程量速度来控制的
单环控制的是速度量

1 PID双环控制

在这里插入图片描述
位置环做为外环，速度环作为内环。外环的输出值作为内环的目标值，外环计算一次pid，根据pid公式可以知道，当离位置目标越来越近时，第一个误差(外环误差)就越来越小，以至于输出的内环目标值就越来越小，所以最终达到的效果就是，离目标值越近，速度越小。（理想情况下，要调节好pid参数，不然系统也会崩溃）

双环控制的时候，外环PID参数调节幅度不要太大，这对于整个曲线的影响很大

代码实现步骤：
① PID参数结构体：定义位置、速度闭环的PID参数结构体变量

② 初始化PID参数：把目标值、期望值、累计偏差清零，配置PID系数
在这里插入图片描述

③ 设置目标位置：只要设置外环的，内环的不用设置，因为内环的目标值，就是外环的输出值。

④ PID双环控制
在定时器中断（1ms）里，每50ms计算一次当前编码器的总计数值，并通过这个值进行外环PID
（位置环）计算，得到目标速度，要经过速度限幅(防止速度过快)，然后存放到g_motor_data.motor_pwm变量(临时存放而已)，根据目标速度，再进行速度环PID计算，最终得出要输出的pwm比较值，存放g_motor_data.motor_pwm变量(最终存放)，然后再限制pwm比较值输出
在这里插入图片描述

3 PID双环控制详细解析

如果采用PID双环控制，控制的其实就是加速度。如果直接输入目标位置，输出当前位置，控制直接是用加速度来控制这个位置显然是不稳定的。所以我们采用双环，用外环来输出目标速度，用内环来控制加速度从而来控制位置
总体流程：目标位置→系统1→目标速度→系统2→加速度→当前位置和速度→反馈回系统1和2

外环：目标位置→系统1→目标速度→反馈给系统1

外环控制的是速度，也就是通过输入目标位置，来控制速度，从而反馈给系统，当我们把目标速度调的比较稳定后，再把此输出的目标速度当作内环的目标值传进内环中

内环：目标速度→系统2→加速度→当前位置→反馈给系统2

内环是把外环的目标速度作为目标值，根据当前的速度控制加速度从而向目标加速度靠近，最后再把输出值作为反馈值

4 双环PID控制器的C++代码实现

float outer_pid_controller(float setpoint, float input, float kp, float ki, float kd, float dt) {static float integral = 0;static float prev_error = 0;float error = setpoint - input;// 计算积分项integral += error * dt;// 计算微分项float derivative = (error - prev_error) / dt;// 计算输出float output = kp * error + ki * integral + kd * derivative;// 更新上一个误差prev_error = error;return output;
}float inner_pid_controller(float setpoint, float input, float kp, float ki, float kd, float dt) {static float integral = 0;static float prev_error = 0;float error = setpoint - input;// 计算积分项integral += error * dt;// 计算微分项float derivative = (error - prev_error) / dt;// 计算输出float output = kp * error + ki * integral + kd * derivative;// 更新上一个误差prev_error = error;return output;
}float double_pid_controller(float setpoint, float input, float outer_kp, float outer_ki, float outer_kd, float inner_kp, float inner_ki, float inner_kd, float dt) {// 计算外环控制器输出float outer_output = outer_pid_controller(setpoint, input, outer_kp, outer_ki, outer_kd, dt);// 计算内环控制器输出float inner_output = inner_pid_controller(outer_output, input, inner_kp, inner_ki, inner_kd, dt);return inner_output;
}

outer_pid_controller和inner_pid_controller分别是外环和内环PID控制器的实现函数。double_pid_controller函数则是将两个PID控制器串联起来，实现双环PID控制器。其中，setpoint是设定值，input是输入值，outer_kp、outer_ki和outer_kd是外环控制器的比例、积分和微分系数，inner_kp、inner_ki和inner_kd是内环控制器的比例、积分和微分系数，dt是采样时间。该函数返回内环PID控制器的输出值。

百度Apollo纵向控制原理如下所示，该图可以为纵向控制器的设置提供参考：
百度Apollo纵向控制框架

可以看出纵向控制是基于Frenet坐标系的，位置跟踪控制器采用P控制器实现车辆位置闭环控制，速度跟踪控制器实现速度闭环控制，根据车辆的俯仰角得出坡道加速度补偿，以及预览点的加速度实现加速度开环控制。基于加速度和定位反馈纵向速度查找油门制动标定表得到油门和刹车的控制量，从而实现车辆的纵向控制。

6 油门刹车标定表

纵向控制逻辑：油门 --> 功率 --> 转速 / 扭矩 --> 车速 / 车加速度 --> 车加速

找到油门和v，a对应的关系
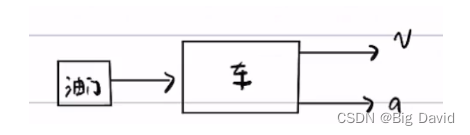
在这里插入图片描述
做实验，踩不同的油门，得到不同的v，a曲线

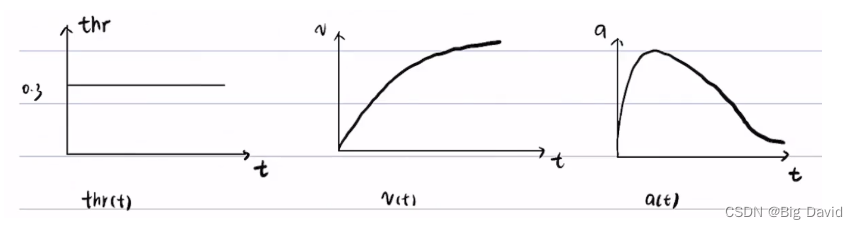
对于一个throttle，不同的时间 t 得到一系列v、a点，v，a可以合并，得到v，a曲线

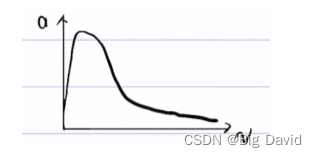
不同的throttle会得到不同的v、a曲线

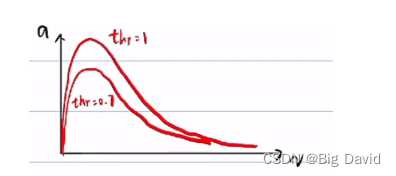
使用不同的throttle做实验，可以得到一个三维曲面
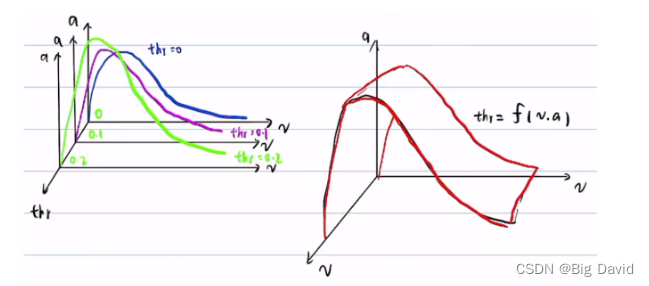
在这里插入图片描述
通过做实验，得到大量的（v，a，throttle）的三维点，从而拟合出throttle = f(v,a)