题目描述：
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例 1：

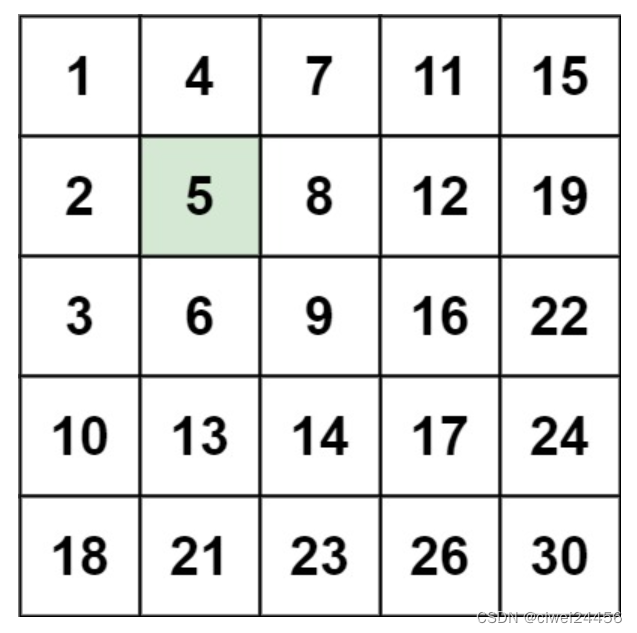
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

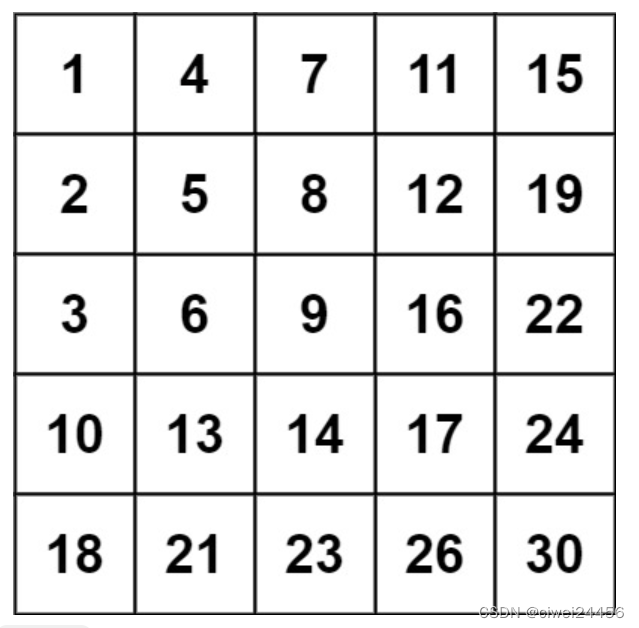
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示：
m==matrix.length
n == matrix[i].length
1 <= n, m <= 300
-109 <= matrix[i][j] <= 109
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-109 <= target <= 109

思路：
通过从 “根节点” 开始搜索，遇到比 target 大的元素就向左，反之向右，即可找到目标值 target 。

“根节点” 对应的是矩阵的 “左下角” 和 “右上角” 元素，本文称之为 标志数 ，以 matrix 中的 左下角元素 为标志数 flag ，则有:
若 flag > target ，则 target 一定在 flag 所在 行的上方 ，即 flag 所在行可被消去。
若 flag < target ，则 target 一定在 flag 所在 列的右方 ，即 flag 所在列可被消去。

算法流程：
从矩阵 matrix 左下角元素（索引设为 (i, j) ）开始遍历，并与目标值对比：
当 matrix[i][j] > target 时，执行 i-- ，即消去第 i 行元素。
当 matrix[i][j] < target 时，执行 j++ ，即消去第 j 列元素。
当 matrix[i][j] = target 时，返回 true ，代表找到目标值。
若行索引或列索引越界，则代表矩阵中无目标值，返回 false 。
每轮 i 或 j 移动后，相当于生成了“消去一行（列）的新矩阵”， 索引(i,j) 指向新矩阵的左下角元素（标志数），因此可重复使用以上性质消去行（列）。

python：

class Solution:def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:i,j=len(matrix)-1,0while i >=0 and j<len(matrix[0]):if matrix[i][j]>target:i-=1elif matrix[i][j]<target:j+=1else:return Truereturn False