目录

一、确定与随机

二、连续与离散

三、周期与非周期

判断是否为周期函数

离散信号的周期

结论

四、能量与功率

定义

结论

五、因果与反因果

六、阶跃函数

定义

性质

七、冲激函数

 定义

重要关系

作用

---

一、确定与随机

确定信号：可以确定时间函数表示的信号。

随机信号：不可以确定时间函数表示的信号。

二、连续与离散

连续时间信号：连续时间范围内（-∞<t<+∞）有定义的信号，简称连续信号。若其函数值也连续，常称为模拟信号（值域连续）。

图2.1 连续信号

离散时间信号：仅在一些离散的瞬间才有定义的信号，简称离散信号。当取值为规定数值时，常称为数字信号（值域不连续）。

图2.2 数字信号 

连续信号变为离散信号：（AD转换）：如果想让一个连续信号进入计算机，需要让连续信号（模拟信号）变为离散信号（数字信号）。这是我们会用到连续采样的方法。

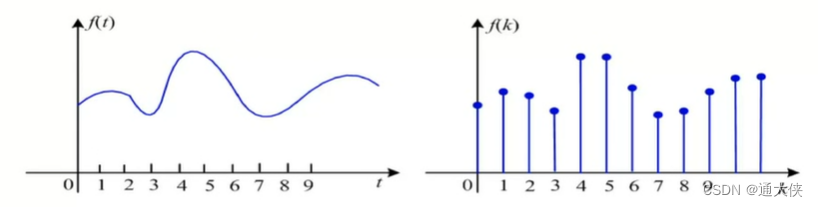
图2.3 连续信号变为离散信号 

离散信号变为连续信号（DA转换）：此法主流有两种表示。第一种是零阶保持法；第二种是分段线性法。

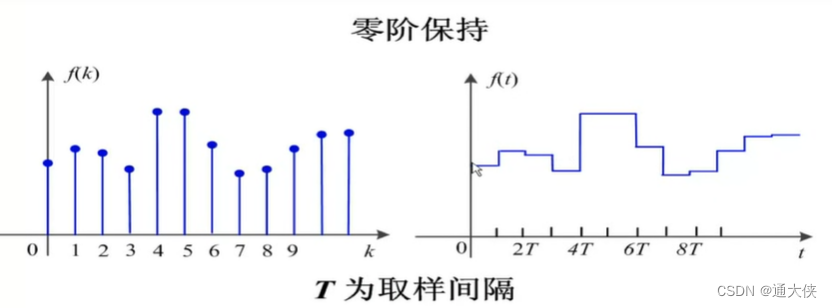
图2.4 零阶保持法 

图2.5 分段线性法 

三、周期与非周期

周期与非周期的概念我们已经非常熟悉了，这里不再过多赘述。

判断是否为周期函数

m个周期函数合成为一个新函数的周期，表示为       

判断方法：两个周期信号的周期分别为与，若与是有理数，则周期信号之和仍然是周期信号，其周期为与的最小公倍数。

例题：判断函数是否为周期函数，若是，周期是多少？

：

：

所以是周期信号，其周期为2π

拓展：若函数是三个周期函数合成的，怎样判断它是否为周期函数，函数的周期是多少？

假设合成后的函数是周期为T的周期函数，那么可得到：

消去分子T，再乘2π，可得到：

 

三个以上周期信号的合成仍适用。

离散信号的周期

f(k)是离散周期信号，N为周期。表示为：

例题：判断正弦序列f(k)=sin(βk）是否为周期信号，若是，确定其周期，式中β为数字角频率，单位：rad。

解：假设f(k)是周期信号，那么可得到：

f(k)=sin(βk)=sin(βk+2mπ)，m=0，±1，±2...

     

       

结论

①为整数时，正弦序列具有周期

②为有理数时，正弦序列仍具有周期性，但周期是，M取使N为整数的最小整数。

③为无理数时，正弦序列为非周期序列。

连续正弦信号一定是周期信号，而正弦序列不一定是周期序列；两连续周期信号之和不一定是周期信号，而两周期序列之和一定是周期序列。

四、能量与功率

定义

图4.1 能量的定义 

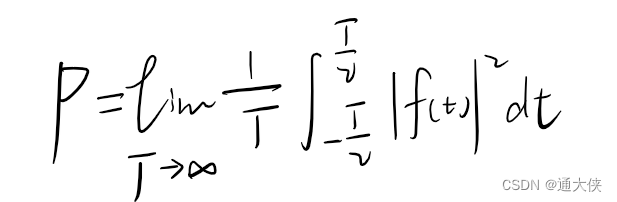
图3.2 平均功率的定义 

能量有限信号：信号的能量E<∞，简称能量信号，此时平均功率P=0。

功率有限信号：信号的功率P<∞，简称功率信号，此时能量E=∞。

结论

①时限信号（仅在有限时间区间不为零）为能量信号；

②周期信号属于能量信号；

③非周期信号可能是能量信号，也可能是功率信号；

④有些信号既不是能量信号也不是功率信号，比如指数函数。

五、因果与反因果

因果信号：，f(t)=0的信号（即t0时接入系统的信号），比如阶跃信号。

反因果信号：，f(t)=0的信号（除0信号外）。

六、阶跃函数

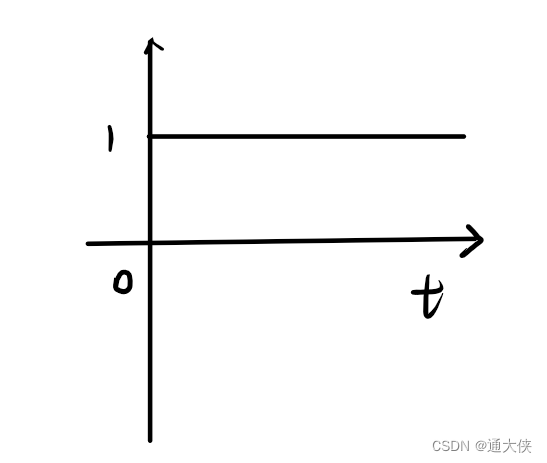
图6.1 单位阶跃函数 

定义

图6.2 阶跃函数的定义 

性质

①表示分段常量信号；

②表示信号的作用区间；

③积分

七、冲激函数

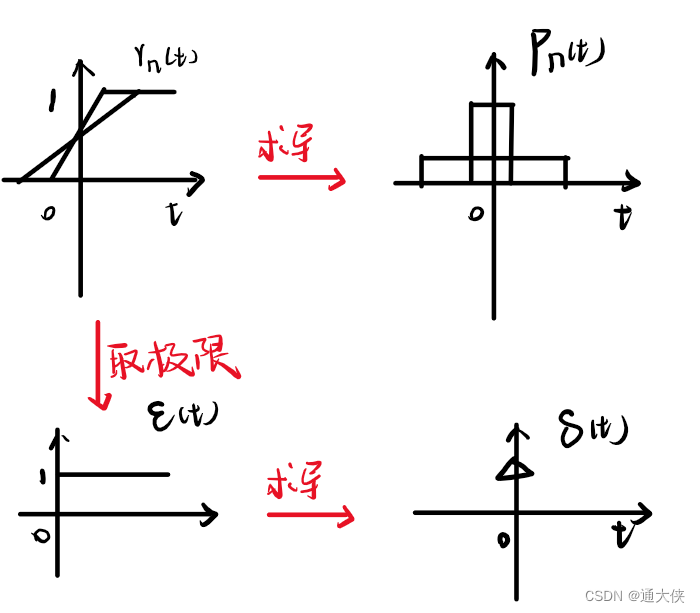
图7.1 几种函数图形 

 定义

冲激函数是奇异函数，它是对强度极大，作用时间极短的物理量的理想化模型，由狄拉克提出 。

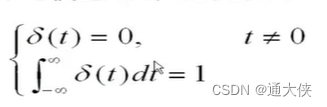
 图7.2 冲激函数的函数

理解：高度无穷大，宽度无穷小，面积为1的对称窄脉冲

图7.3 

图7.3中间的Pn(t)叫“门函数”

重要关系

作用

冲激函数可以描述间断点的导数

图7.4