一个例子

相比凉爽的天气，蟋蟀在较为炎热的天气里鸣叫更频繁。
现有数据如下图，请预测鸣叫声与温度的关系。

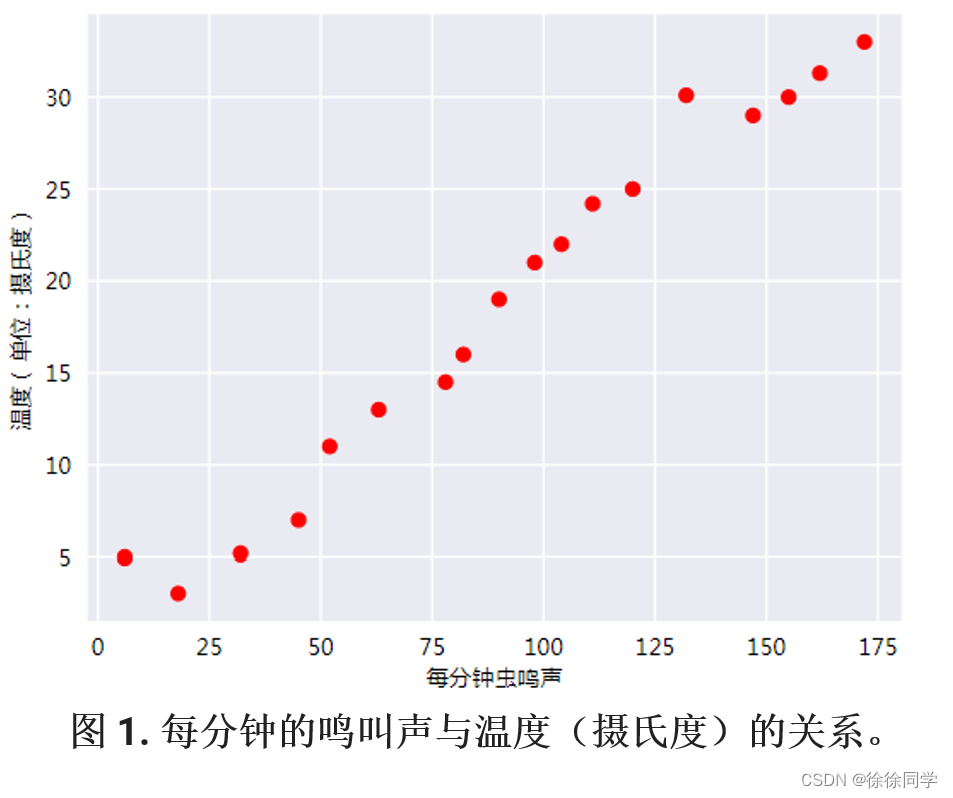
线性回归

如图这种由点确定线的过程叫回归，既找出因变量和自变量之间的关系

y = mx + b

y指的是温度（摄氏度），即我们试图预测的值
m指的是直线的斜率
x指的是每分钟的鸣叫声次数，即输入特征的值
b指的是y轴截距

机器学习中的表达

y=𝑤𝑥+𝑏

x 特征（feature)
y 预测值（target）
w 权重（weight）
b 偏差（bias）

样本（samples） （x，y）

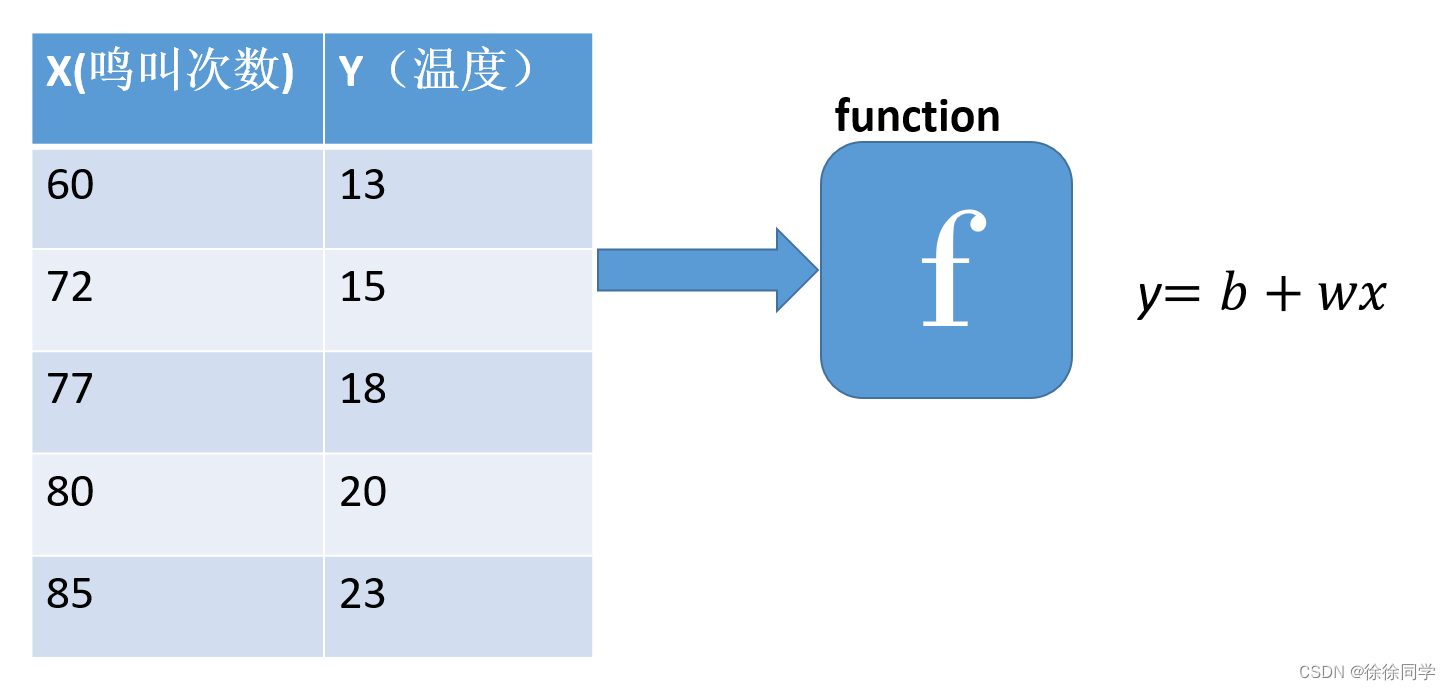
如何找出最优的函数 ， 即找出一组最佳的w和b？
首先需要对函数的好坏进行评价

评价函数好坏的度量：损失（Loss）

反应模型预测（prediction）的准确程度。

如果模型（model）的预测完全准确，则损失为零。
训练模型的目标是从所有样本中找到一组平均损失 “较小” 的权重和偏差。

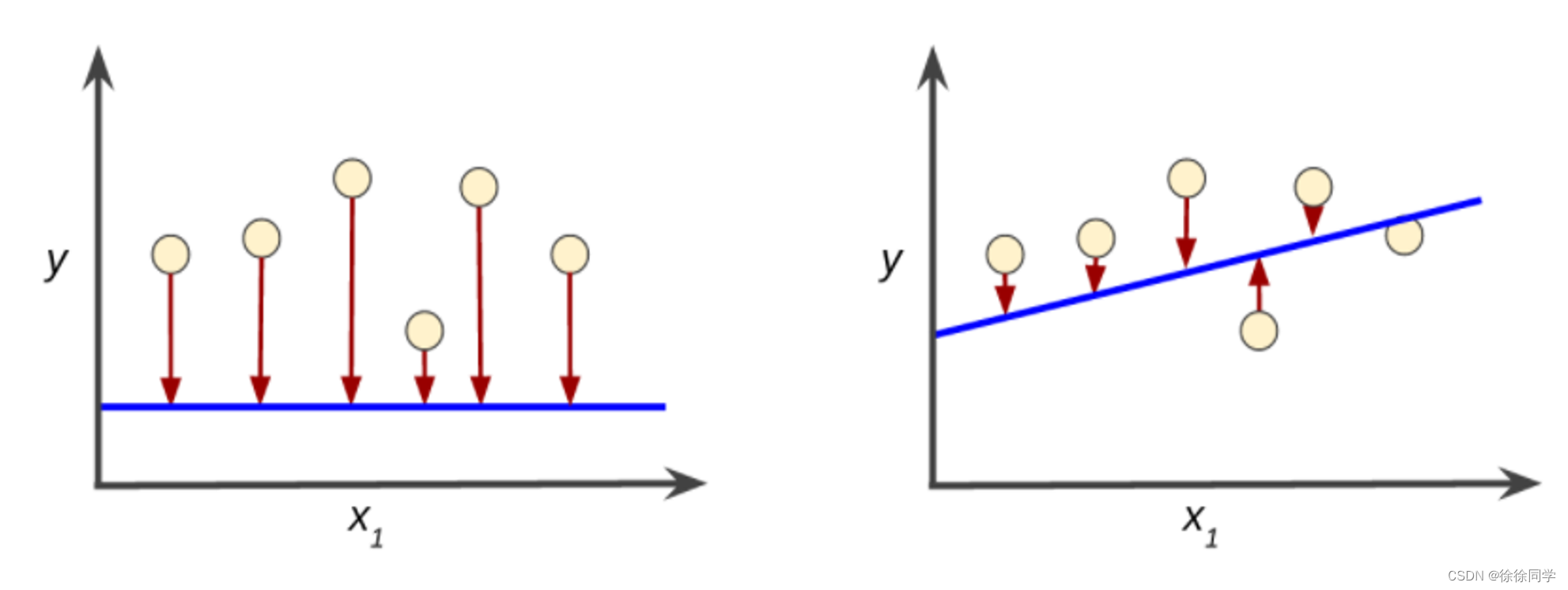
显然，相较于左侧曲线图中的蓝线，右侧曲线图中的蓝线代表的是预测效果更好的模型

损失函数（Loss function）

损失函数是指汇总各样本损失的数学函数。

· 平方损失（又称为 L₂ 损失）
· 单个样本的平方损失= ( observation - prediction(x) )² = ( y - y’ )²
· 均方误差 (mean-square error, MSE) 指的是样本的平均平方损失

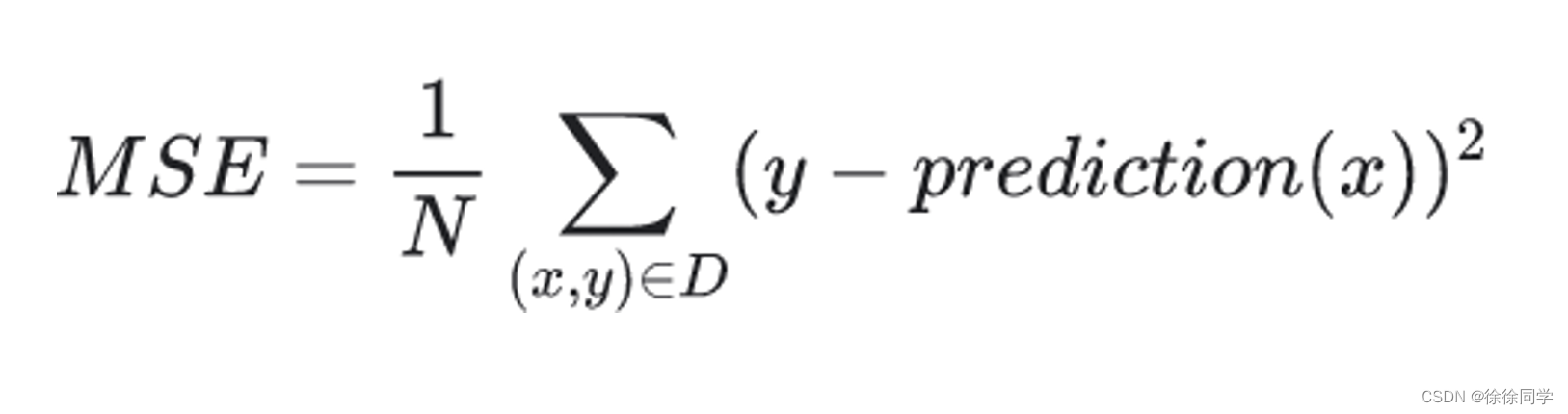
哪个数据集的均方误差 (MSE) 高

以下两幅图显示的两个数据集，哪个数据集的均方误差 (MSE) 较高？

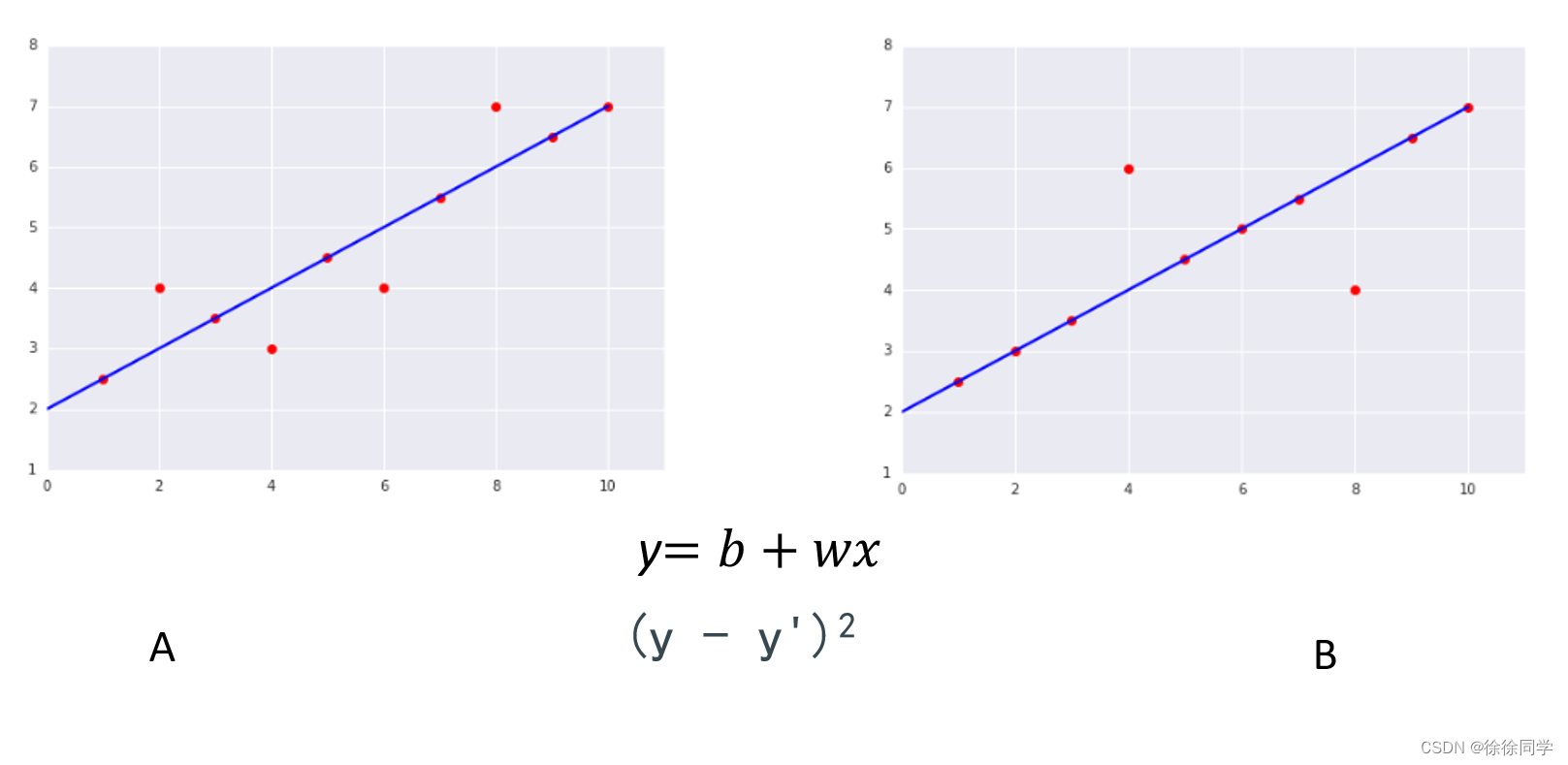
B图线上的 8 个样本产生的总损失为 0。不过，尽管只有两个点在线外，但这两个点的离线距离依然是左图中离群点的 2 倍。平方损失进一步加大差异，因此两个点的偏移量产生的损失是一个点的 4 倍。
· 根据损失函数的定义
· 对于A：MSE = (0² + 1² + 0² + 1² + 0² + 1² + 0² + 1² + 0² + 0²)/10 = 0.4
· 对于B：MSE = (0² + 0² + 0² + 2² + 0² + 0² + 0² + 2² + 0² + 0²)/10 = 0.8

→因此B的MSE较高。

如何找出最优b和w?

定义了损失函数，我们就可以评价任一函数的好坏，下一步如何找出最优b和w?
靠猜~

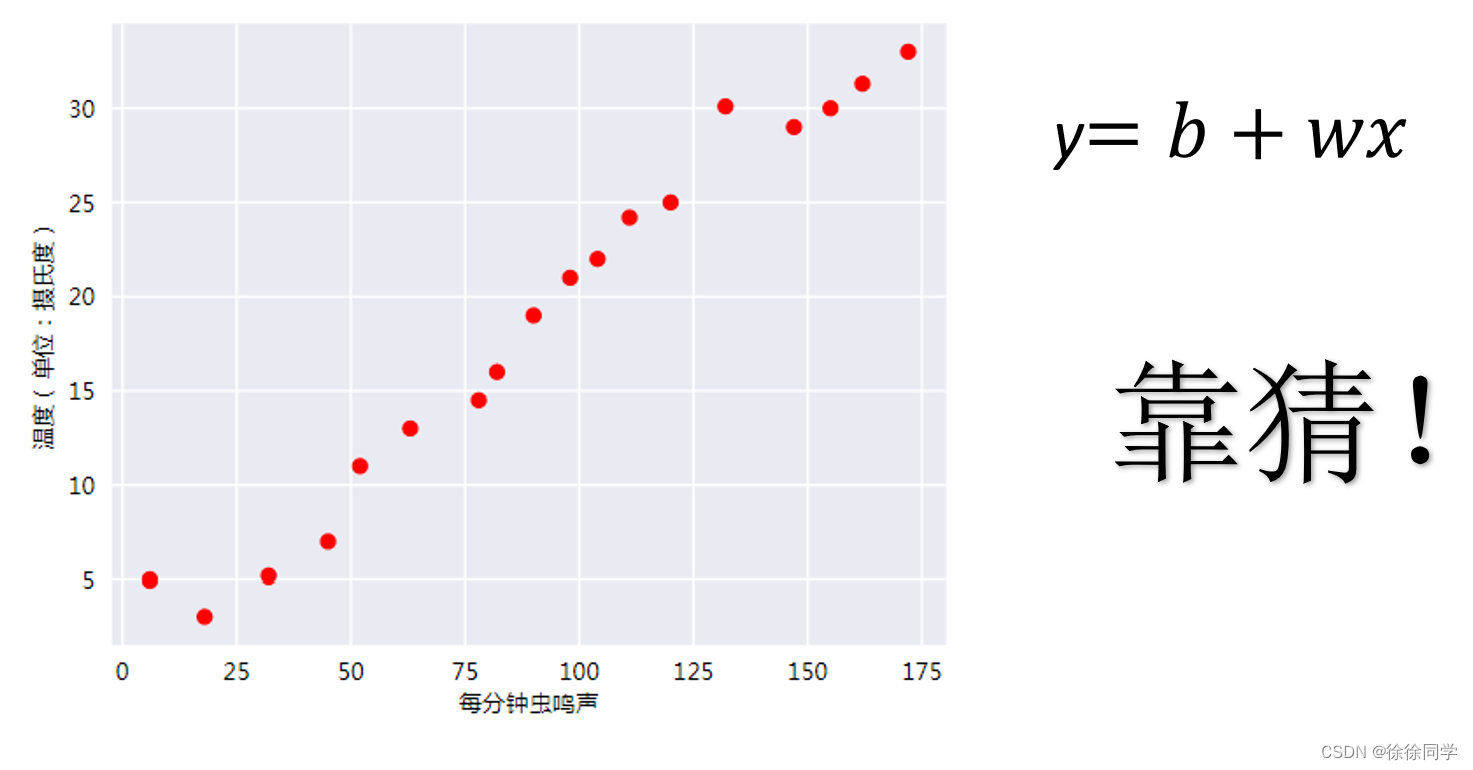
像猜价格游戏，参与者给出初始价钱，通过“高了”或“低了”的提示，逐渐接近正确的价格。

寻找最优b和w

1. 首先随机给出一组参数b=1，w=1 
2. 评价这组参数的好坏，例如用MSE 
3. 改变w和b的值
4. 转到步骤2，直到总体损失不再变化或变化极其缓慢为止，该模型已收敛

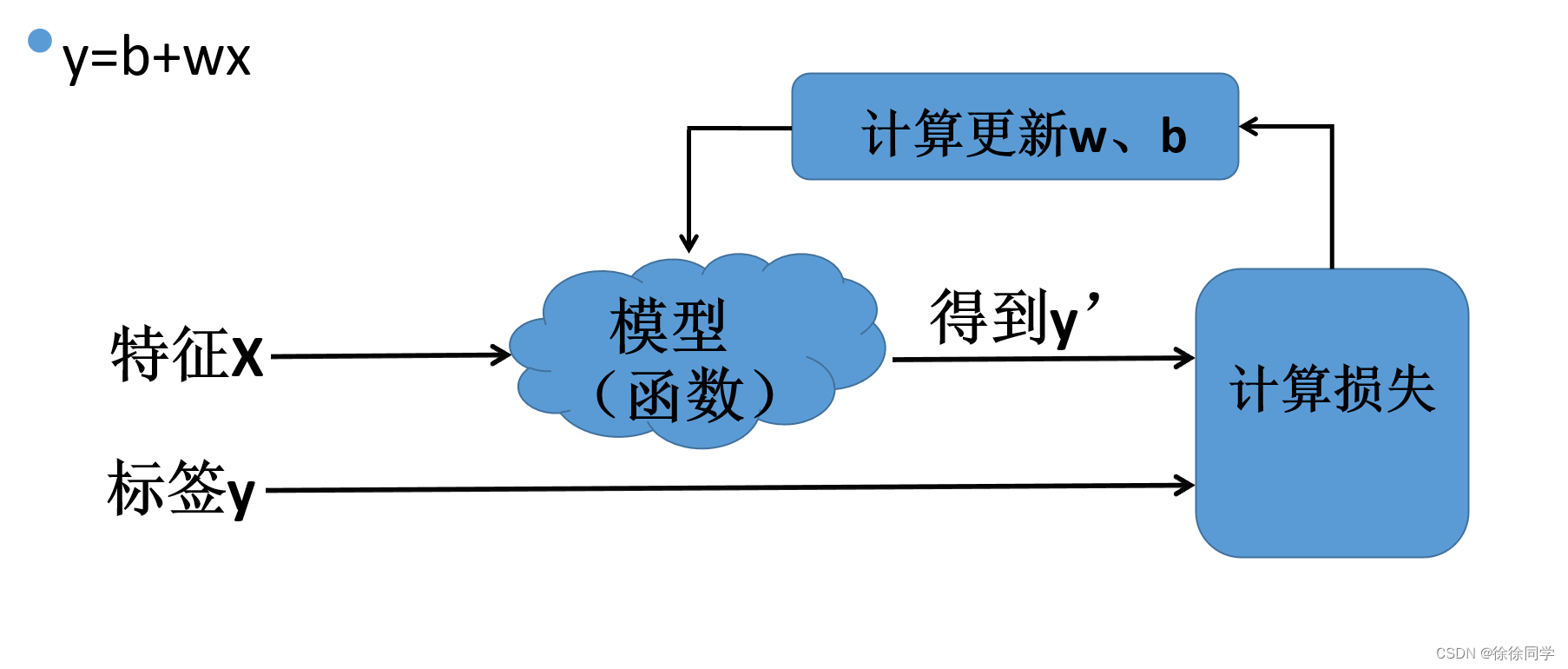
最后一个问题：如何改变w、b ???

如何降低损失 (Reducing Loss)

简化问题，以只有一个参数w为例，所产生的损失Loss与 w 的图形是凸形（convex）。如下所示：

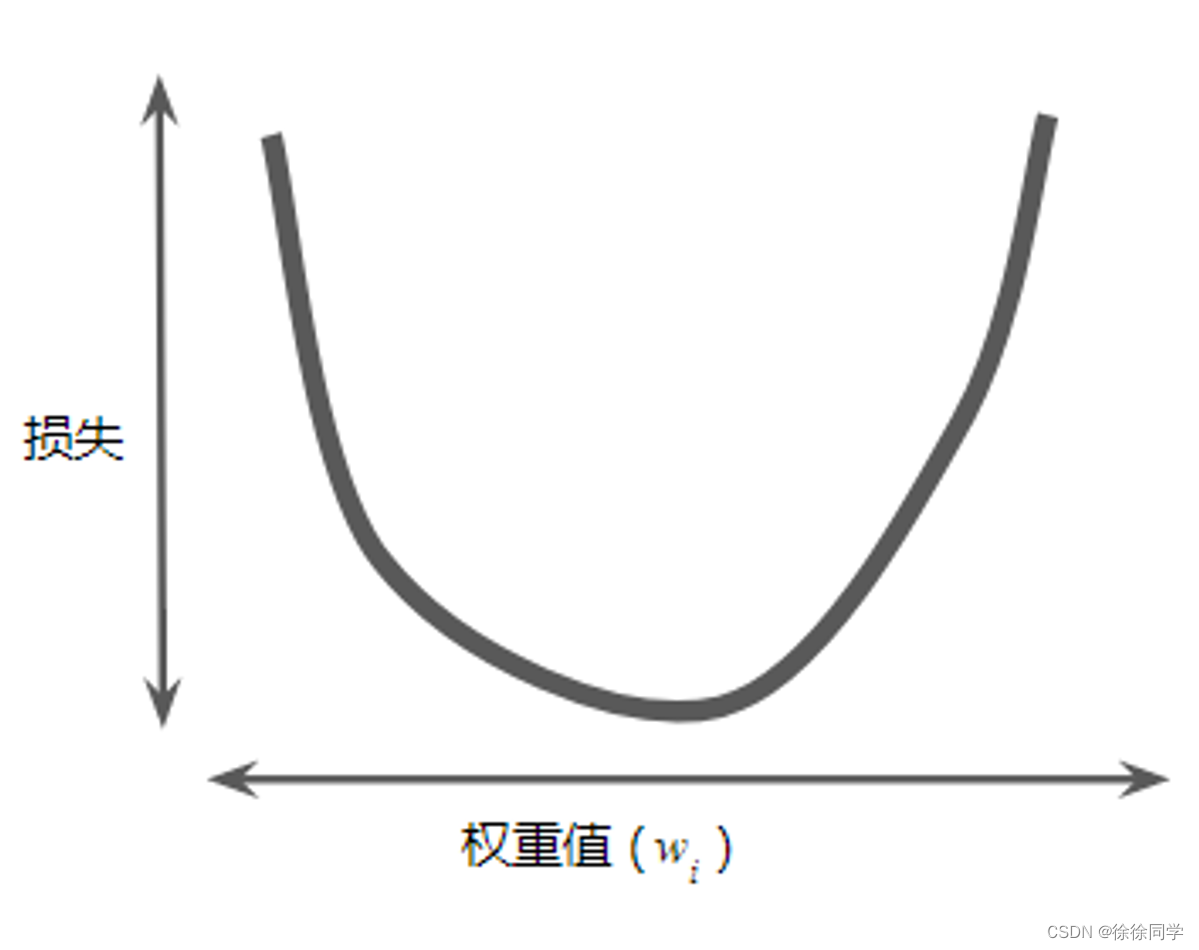
只有一个最低点 → 即只存在一个斜率正好为 0 的位置。
损失函数取到最小值的地方。

但是，如何找到这一点呢？

1. 为w选择一个起点↓ 这里选择了一个稍大于 0 的起点
   

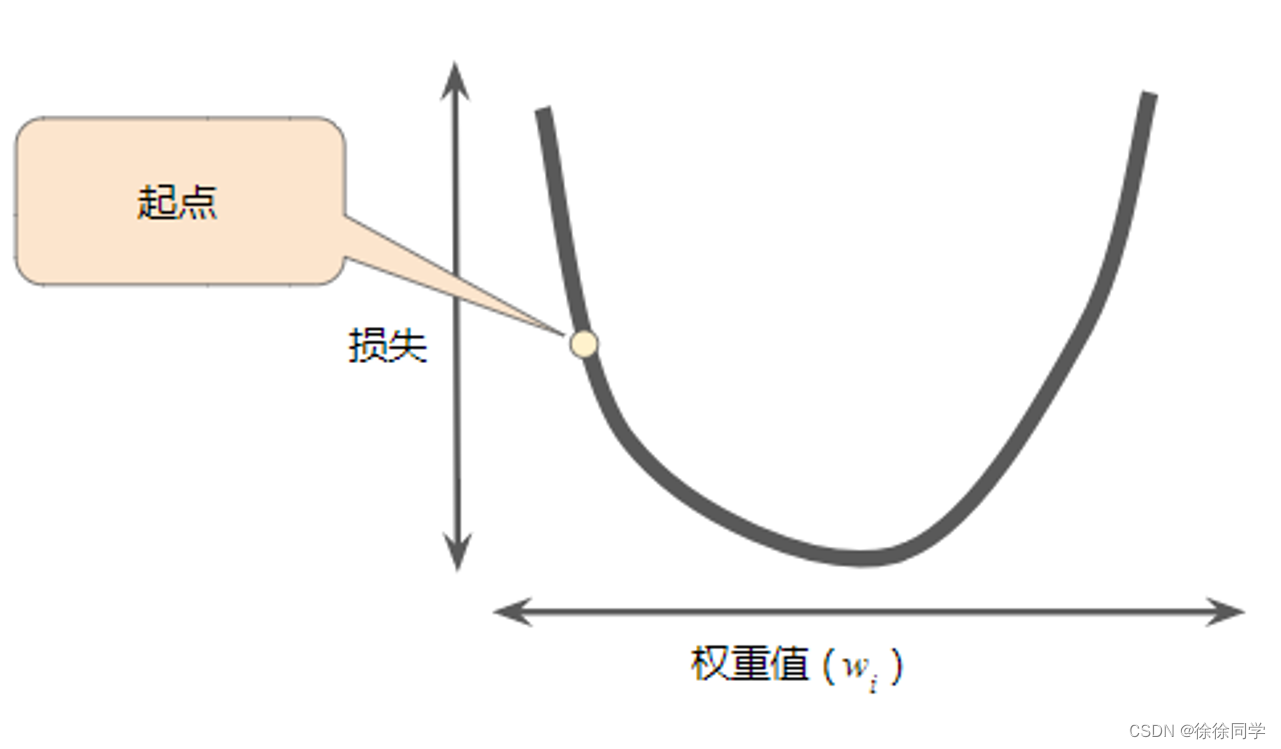
梯度下降法

梯度

· 梯度是偏导数的矢量；有方向和大小。

· 梯度即是某一点最大的方向导数，沿梯度方向函数有最大的变化率
（沿梯度方向函数增加，负梯度方向函数减少）

· 损失Loss相对于单个权重的梯度大小就等于导数f^’(x)i

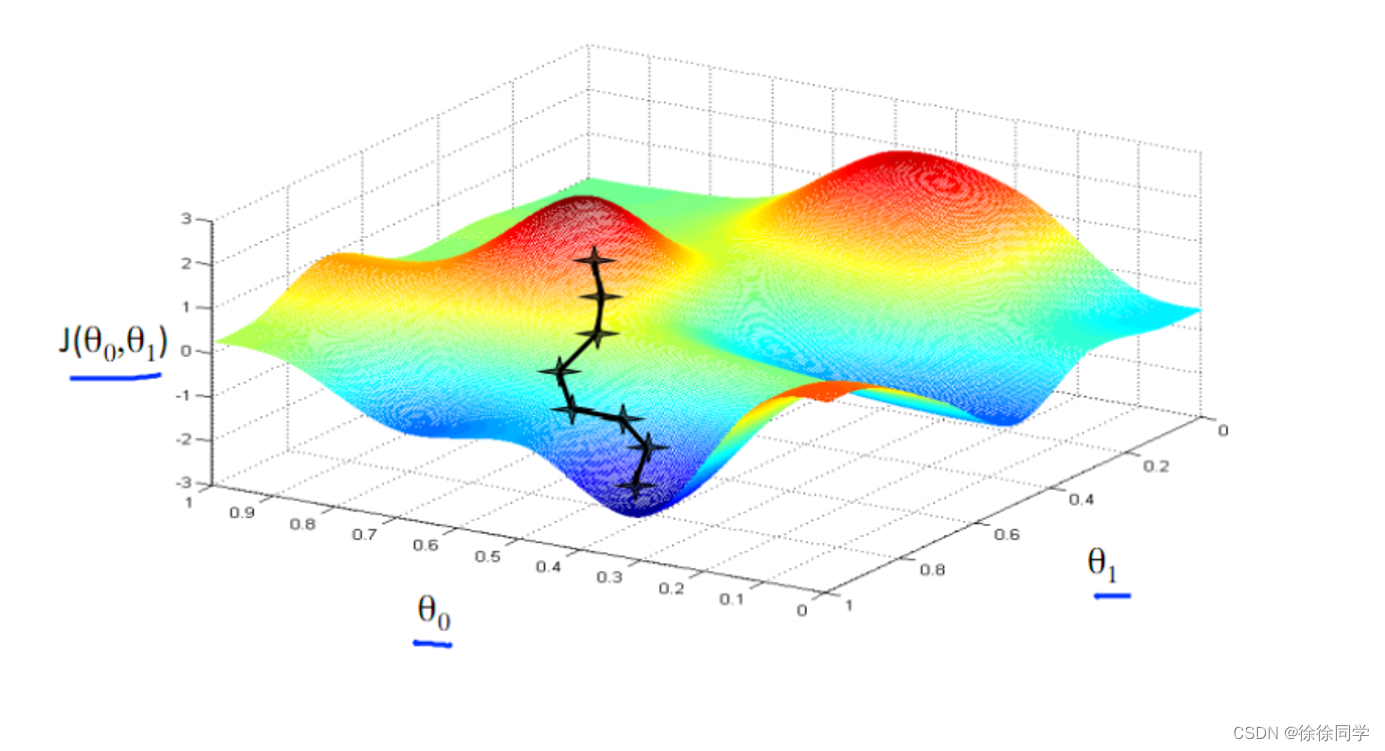
二元函数的梯度：

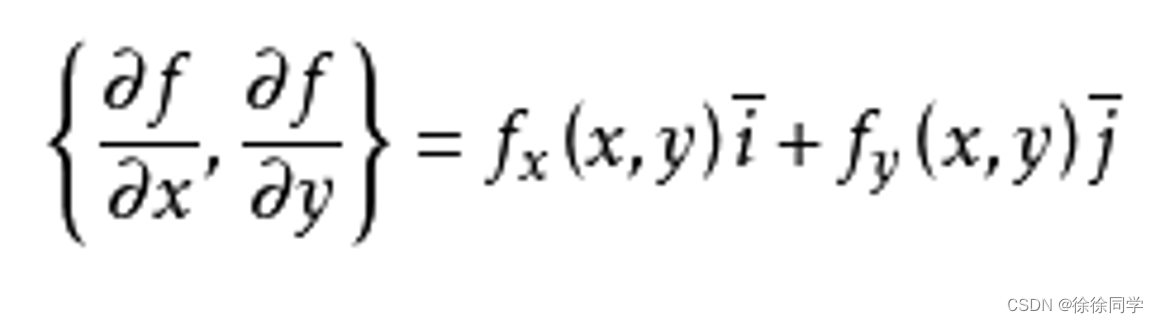
计算梯度f^’(x)i

求导数，即切线的斜率，在这个例子中，是负的，因此负梯度是w的正方向。

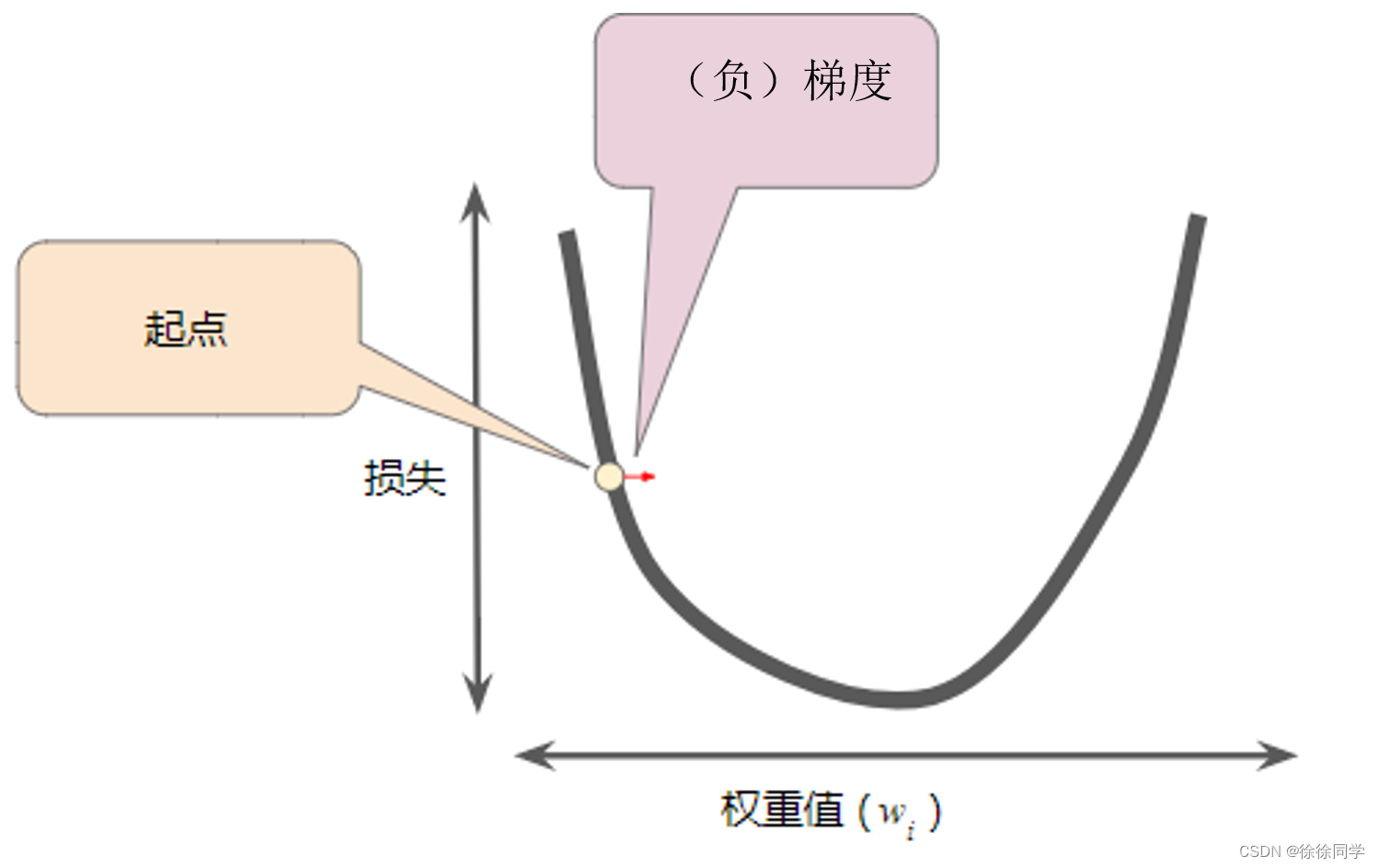
梯度下降法（gradient descent）

w=w-lr*w_grad

lr (learning rate，学习速率)

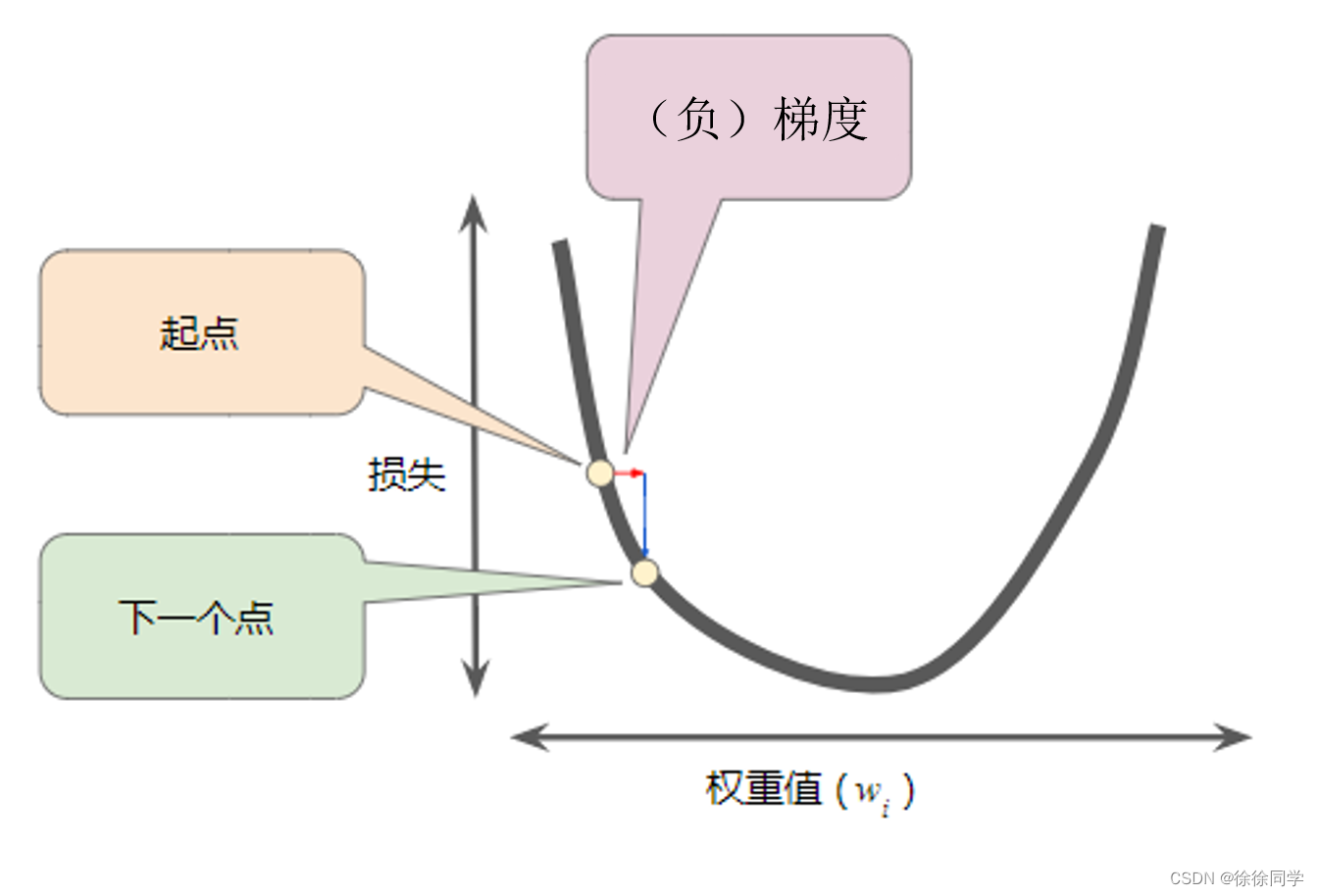
然后，重复此过程，逐渐接近最低点。

⭐负梯度指向损失函数下降的方向

学习速率（Learning rate）

通常梯度下降法用梯度乘以学习速率（步长），以确定下一个点的位置：

w=w-lr*w_grad

例如，如果学习速率为 0.01，梯度大小为 2.5，则：
w=w-0.01*2.5

学习速率是机器学习算法中人为引入的，是用于调整机器学习算法的旋钮，这种称为超参数。

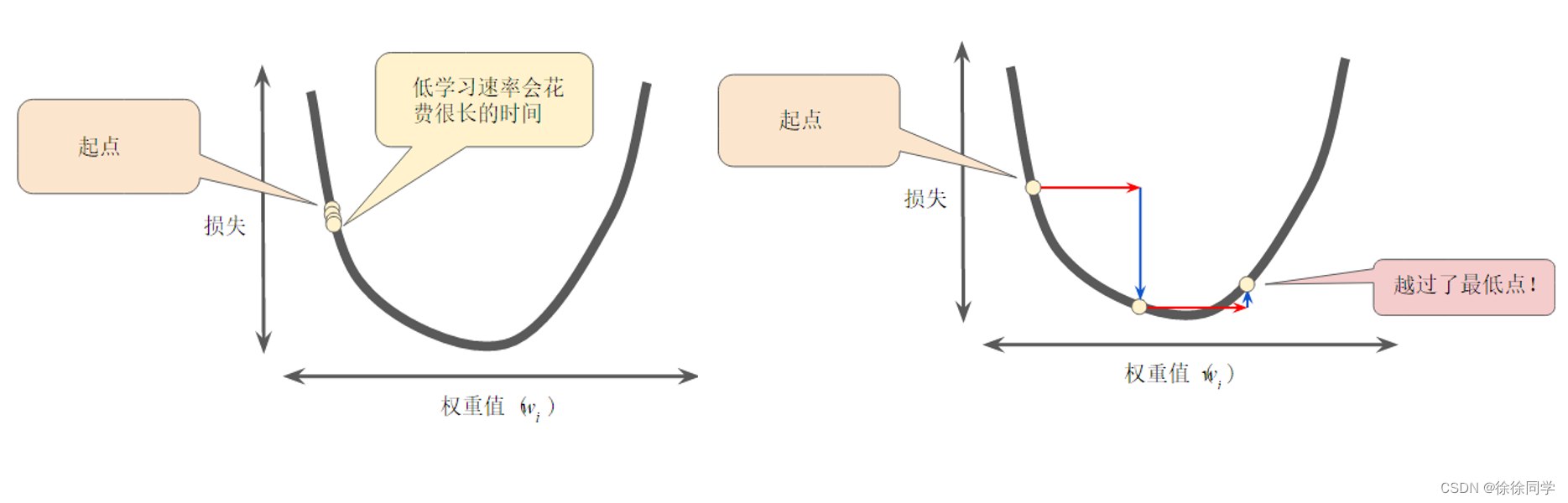
金发女孩原则（Goldilocks principle）

每个回归问题都存在一个“Goldilocks principle”学习速率，该值与损失函数的平坦程度相关。 例如，如果损失函数的梯度较小，则可以采用更大的学习速率，以补偿较小的梯度并获得更大的步长。

（西方有一个儿童故事叫 “ The Three Bears（金发女孩与三只小熊）”，迷路了的金发姑娘未经允许就进入了熊的房子，她尝了三只碗里的粥，试了三把椅子，又在三张床上躺了躺。最后发现不烫不冷的粥最可口，不大不小的椅子坐着最舒服，不高不矮的床上躺着最惬意。道理很简单，刚刚好就是最适合的，just the right amount，这样做选择的原则被称为 Goldilocks principle（金发女孩原则）。）

采取恰当学习速率，可以高效的到达最低点，如下图所示：

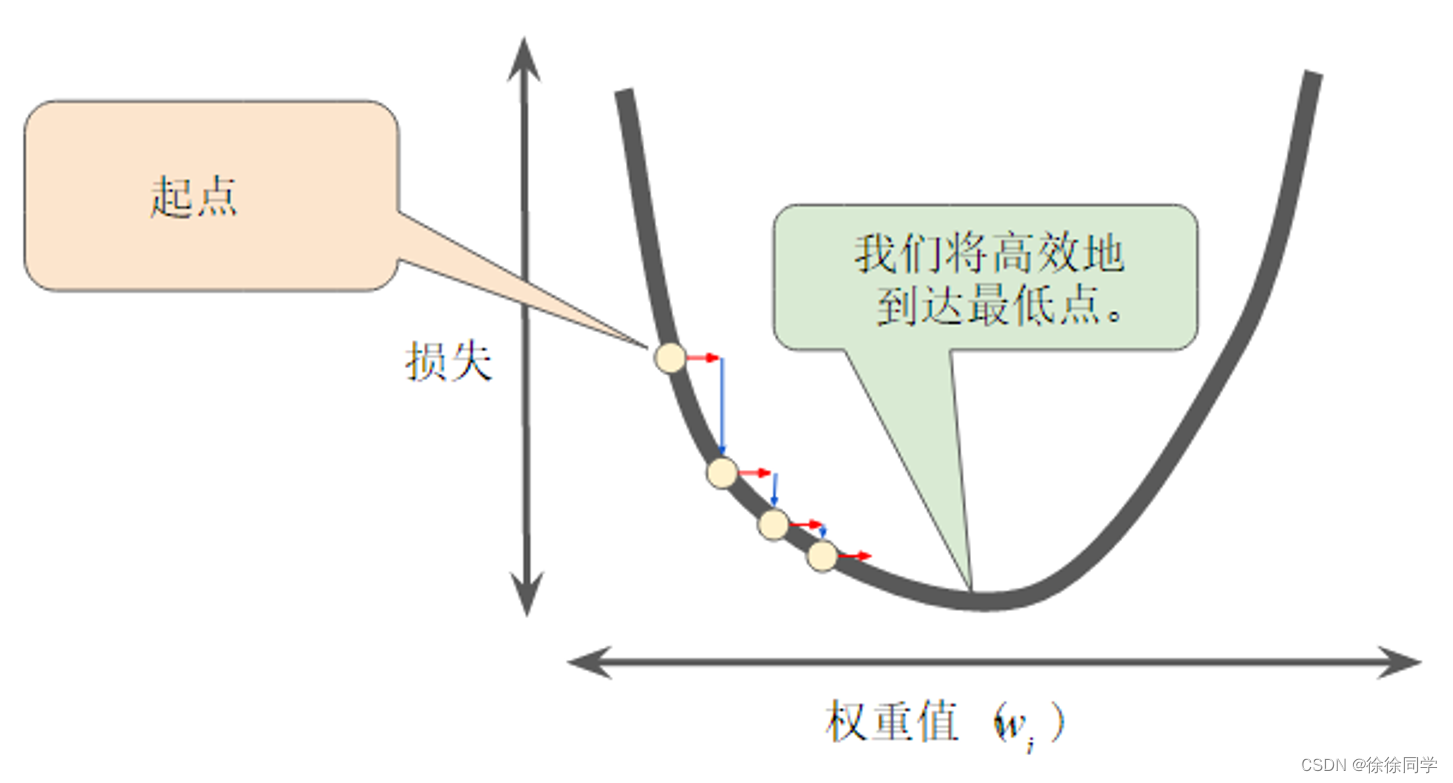
降低损失：优化学习速率-模拟动图

如何训练模型

1. 定义一个函数的集合
2. 给出评价函数好坏的方法
3. 利用梯度下降法找到最佳函数

习题

import numpy as np
import matplotlib.pyplot as pltdef gradient_descent(x, y, theta, learning_rate, epochs):ws = []bs = []for i in range(epochs):y_pred = x.dot(theta)diff = y_pred - yloss = 0.5 * np.mean(diff ** 2)g = x.T.dot(diff)theta -= learning_rate * gws.append(theta[0][0])bs.append(theta[1][0])learning_rate = learning_rate_shedule(i + 1)print(f'第{i + 1}次梯度下降后，损失为{round(loss, 5)}，w为{round(theta[0][0], 5)}，b为{round(theta[1][0], 5)}')if loss < 0.001:breakreturn ws, bsdef learning_rate_shedule(t):return t0 / (t + t1)if __name__ == '__main__':xdata = np.array([8, 3, 9, 7, 16, 5, 3, 10, 4, 6])ydata = np.array([30, 21, 35, 27, 42, 24, 10, 38, 22, 25])x_data = np.array(xdata).reshape(-1, 1)y_data = np.array(ydata).reshape(-1, 1)X = np.concatenate([x_data, np.full_like(x_data, fill_value=1)], axis=1)theta = np.random.randn(2, 1)t0 = 1.5t1 = 1000ws, bs = gradient_descent(X, y_data, theta, learning_rate_shedule(0), 10000)ax = plt.subplot(3, 2, 1)bx = plt.subplot(3, 2, 2)cx = plt.subplot(3, 1, (2, 3))# 散点+预测线ax.scatter(x_data, y_data)x = np.linspace(x_data.min() - 1, x_data.max() + 1, 100)y = ws[-1] * x + bs[-1]ax.plot(x, y, color='red')ax.set_xlabel('x')ax.set_ylabel('y')#w,b变化x = np.arange(1, len(ws) + 1)bx.plot(x, ws, label='w')bx.plot(x, bs, label='b')bx.set_xlabel('epoch')bx.set_ylabel('change')bx.legend()#等高线def get_loss(w, b):return 0.5 * np.mean((y_data - (w * x_data + b)) ** 2)b_range = np.linspace(-100, 100, 100)w_range = np.linspace(-10, 10, 100)losses = np.zeros((len(b_range), len(w_range)))for i in range(len(b_range)):for j in range (len(w_range)):losses[i, j] = get_loss(w_range[j], b_range[i])cx.contour(b_range, w_range, losses, cmap='summer')cx.contourf(b_range, w_range, losses)cx.set_xlabel('b')cx.set_ylabel('w')plt.show()