😆😆😆感谢大家的支持~😆😆😆

逻辑回归的应用场景

逻辑回归（Logistic Regression）是机器学习中的 一种分类模型 ，逻辑回归是一种分类算法，虽然名字中带有回归。由于算法的简单和高效，在实际中应用非常广泛☺️

• 广告点击率，预测用户是否会点击某个广告，是典型的二分类问题。逻辑回归可以根据用户的特征（如年龄、性别、浏览历史等）来预测点击概率。
• 是否为垃圾邮件，电子邮件服务提供商使用逻辑回归来判断邮件是否为垃圾邮件，根据邮件内容特征和发送者信息来进行分类。
• 是否患病，在医疗领域，逻辑回归可以帮助预测患者是否有发病的风险，例如基于患者的各种生理指标来预测糖尿病或冠心病的风险。
• 信用卡账单是否会违约，金融机构利用逻辑回归模型来评估信用卡用户是否存在违约风险，这通常涉及对用户的信用历史、交易行为等进行分析。

逻辑回归是一种用于分类问题的统计模型，特别是适合于处理二分类问题。

逻辑回归的输入🥰

逻辑回归模型的核心在于它使用了一个线性方程作为输入，这个线性方程通常称为logit函数。具体来说，逻辑回归模型首先通过一个线性方程对输入特征进行加权求和，然后使用Sigmoid函数将这个线性方程的结果映射到(0,1)区间内，从而得到一个概率值。这个过程可以用以下数学公式表示：

[ P(y=1|x) = \frac{1}{1 + e^{-(\beta_0 + \beta_1x_1 + \ldots + \beta_nx_n)}} ]

激活函数 

Sigmoid函数的数学表达式通常写为 ( sigma(x) = \frac{1}{1 + e^{-x}} )，其中 ( x ) 是输入变量。

• 回归的结果输入到sigmoid函数当中

逻辑回归的损失，称之为 对数似然损失 

在逻辑回归中，损失函数是用来度量预测值与真实值之间的差异的。具体来说，逻辑回归通常使用的损失函数是交叉熵（Cross Entropy），这是一种衡量两个概率分布之间差异的函数。交叉熵损失函数可以写成以下形式：

[ L(y, p) = -frac{1}{N} \sum_{i=1}^{N} [y_i \log(p_i) + (1 - y_i) \log(1 - p_i)] ]

其中，( y_i ) 是样本的真实标签（0或1），( p_i ) 是模型预测该样本为正例的概率，N是样本数量。这个损失函数的目的是使得模型输出的概率尽可能接近真实标签。当模型预测的概率与真实标签一致时，损失函数的值会很小；反之，如果预测的概率与真实标签相差较大，则损失函数的值会比较大。

优化同样使用梯度下降优化算法，去减少损失函数的值。这样去更新逻辑回归前面对应算法的权重参数，提升原本属于1类别的概率，降低原本是0类别的概率。 

from sklearn.linear_model import SGDRegressor# 创建SGDRegressor实例
estimator = SGDRegressor(max_iter=1000)# 使用训练数据拟合模型
estimator.fit(x_train, y_train)

 案例🤔

 sklearn.linear_model.LogisticRegression(solver='liblinear', penalty=‘l2’, C = 1.0)

💎l2作为正则化项（惩罚项），以及C=1.0作为正则化强度的倒数。 

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegressionnames = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape','Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin', 'Normal Nucleoli', 'Mitoses', 'Class']data = pd.read_csv("wisconsin.data")
data.head()x = data.iloc[:, 1:10]
x.head()
y = data["Class"]
y.head()x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)estimator = LogisticRegression()
estimator.fit(x_train, y_train)y_predict = estimator.predict(x_test)
y_predict
estimator.score(x_test, y_test)

分类评估指标

ROC曲线（Receiver Operating Characteristic Curve）：ROC曲线描绘了不同阈值下的真正例率和假正例率，用于评估模型在不同阈值下的表现。在机器学习领域，ROC曲线和AUC指标广泛应用于模型选择和性能评估。

💎ROC曲线，全称为接收者操作特征曲线（Receiver Operating Characteristic Curve），是一种用于评估二分类模型性能的图形化工具。它以假正率（False Positive Rate, FPR）为横轴，真正率（True Positive Rate, TPR）为纵轴绘制而成。ROC曲线上每个点反映了在不同判定阈值下，模型对正类和负类样本分类的能力。通过观察ROC曲线，我们可以直观地了解分类器在不同阈值下的性能表现。

💎AUC（Area Under Curve）则是ROC曲线下的面积，用于量化地衡量模型的整体分类性能。AUC的取值范围在0.5到1之间，其中0.5表示模型没有区分能力，而1表示模型具有完美的分类能力。AUC越大，说明模型在区分正负样本上的表现越好。在实际应用中，一个AUC值接近1的模型通常被认为具有较高的预测准确性和可靠性。

1. 正样本中被预测为正样本的概率，即：TPR （True Positive Rate）
2. 负样本中被预测为正样本的概率，即：FPR （False Positive Rate）

ROC 曲线图像中，4 个特殊点的含义：

1. (0, 0) 表示所有的正样本都预测为错误，所有的负样本都预测正确
2. (1, 0) 表示所有的正样本都预测错误，所有的负样本都预测错误
3. (1, 1) 表示所有的正样本都预测正确，所有的负样本都预测错误
4. (0, 1) 表示所有的正样本都预测正确，所有的负样本都预测正确

绘制 ROC 曲线

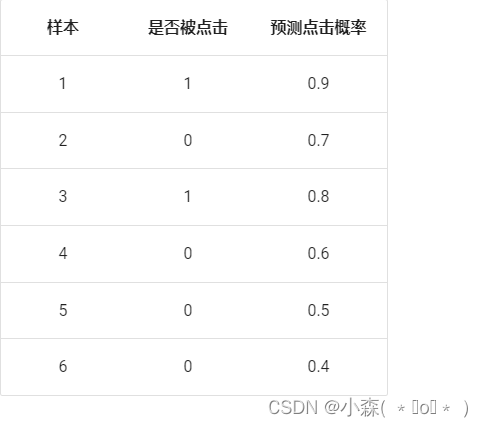
在网页某个位置有一个广告图片或者文字，该广告共被展示了 6 次，有 2 次被浏览者点击了。

 

绘制 ROC 曲线：

阈值：0.9

1. 原本为正例的 1、3 号的样本中 3 号样本被分类错误，则 TPR = ½ = 0.5
2. 原本为负例的 2、4、5、6 号样本没有一个被分为正例，则 FPR = 0

阈值：0.8

1. 原本为正例的 1、3 号样本被分类正确，则 TPR = 2/2 = 1
2. 原本为负例的 2、4、5、6 号样本没有一个被分为正例，则 FPR = 0

 阈值：0.7

1. 原本为正例的 1、3 号样本被分类正确，则 TPR = 2/2 = 1
2. 原本为负类的 2、4、5、6 号样本中 2 号样本被分类错误，则 FPR = ¼ = 0.25

 

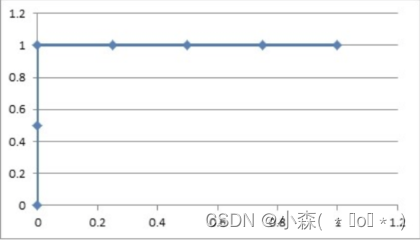
💎 图像越靠近 (0,1) 点则模型对正负样本的辨别能力就越强且图像越靠近 (0, 1) 点则 ROC 曲线下面的面积就会越大。

1. 当 AUC= 1 时，该模型被认为是完美的分类器，但是几乎不存在完美分类器

案例 

y=churn['flag']
x=churn[['contract_month','internet_other','streamingtv']]from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=100)from sklearn import linear_model
lr=linear_model.LogisticRegression()
lr.fit(x_train,y_train)y_pred_train=lr.predict(x_train)
y_pred_test=lr.predict(x_test)
import sklearn.metrics as metrics
metrics.accuracy_score(y_train,y_pred_train)
from sklearn.metrics import roc_auc_score
roc_auc_score(y_test, y_pred_test)    # 网格搜索参数
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import GridSearchCV
kfold = StratifiedKFold(n_splits=5, shuffle=True)
lr = linear_model.LogisticRegression()
param_grid = {'solver': ['newton-cg', 'lbfgs', 'liblinear'],'C': [0.001, 0.01, 1, 10, 100],'class_weight':['balanced']}
search = GridSearchCV(lr, param_grid, cv=kfold)
lr = search.fit(x_train, y_train)

LogisticRegression(class_weight='balanced')参数的作用是在拟合模型时自动调整类别权重，以帮助处理不平衡的数据集。当使用class_weight='balanced'时，Scikit-learn的LogisticRegression会在计算损失函数时自动为每个类分配权重，使得较少出现的类别（少数类）获得更高的权重，以此来平衡各类别之间的样本数量差异。这样做有助于改善模型对少数类的识别能力，特别是在数据集中某些类的样本数量远少于其他类时，这种权重调整可以防止模型偏向于多数类。