还是用之前的猫狗二分类任务举例（这个例子出现在【机器学习300问】第33问中），我们新增一个数值型特征（体重），下表是数据集的详情。如果想了解更多决策树的知识可以看看我之前的两篇文章：
【机器学习300问】28、什么是决策树？
http://t.csdnimg.cn/Tybfj
【机器学习300问】33、决策树是如何进行特征选择的？http://t.csdnimg.cn/iaxSA 这里我就不赘述啦，直接进入正题。
如果我选择用体重特征作为根节点的决策策略，那么我们会面临这样一个问题。
一、什么阈值才能更好的区分数据集？
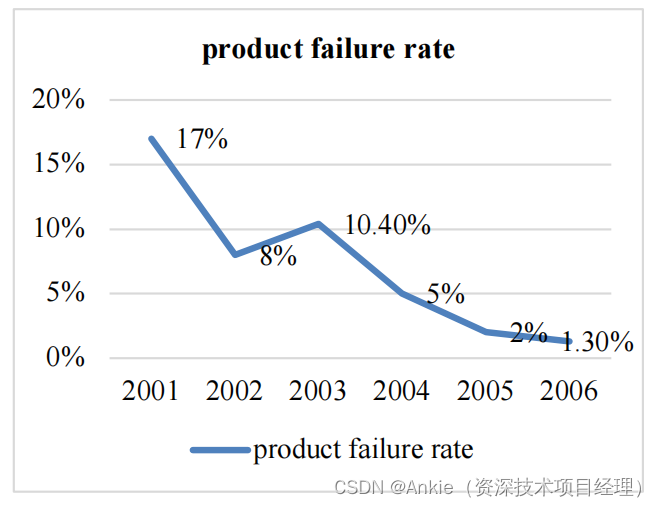
所用到的工具还是信息增益，我们可以将一些列可能比较不错的能区分数据集的阈值列举出来，例如，在连续数值区间上，可以测试每个唯一值或者每隔一定步长选取值作为潜在的阈值，画出下面这样的一幅图。
- 首先，遍历数据集中所有猫和狗的体重值
- 对于每一个可能的体重阈值，将样本集划分为两个子集：一组是体重低于该阈值的动物，另一组是体重等于或高于该阈值的动物
- 计算划分前的数据集的信息熵以及每个子集的信息熵，并根据子集内样本数目的比例加权求和得到条件熵（就像下面这幅图中所示）
- 通过比较不同阈值下所对应的信息增益，选择信息增益最大的那个阈值作为分割点
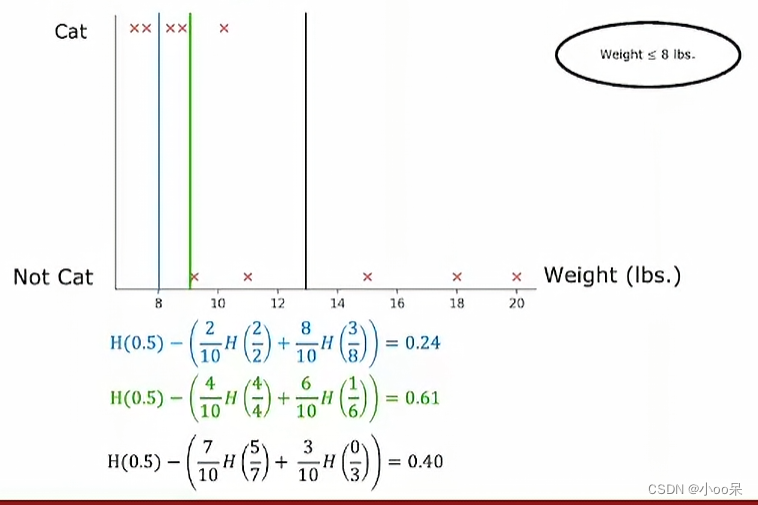
在这个例子中我们最终选定了，体重<=9，作为最合适的阈值，因为此时的信息增益最大。
二、如何停止决策树的分叉？
这里再讲一个知识点，虽然这个知识点和题目无关（偷笑），但因为讲到了信息增益所以补充一个通过信息增益停止构建决策树防止过拟合的方法。决策树停止分叉（即停止生长或停止构建子节点）的常见条件包括但不限于以下几种：
-
最大深度限制：预先设定一个整数值，作为决策树的最大允许深度。当当前节点所在的分支达到这个深度时，无论当前节点的信息增益或其他指标如何，都不再进行分割。
-
最小节点样本数：规定每个内部节点（非叶子节点）所包含的最少样本数量，若某节点划分后某个子节点中的样本数量小于这个阈值，则不再继续分割。
-
信息增益阈值：设置一个信息增益的最小值，如果某个特征划分数据集后的信息增益低于此阈值，则停止该节点的进一步划分。
-
叶子节点数目限制：可以设定决策树允许的最大叶子节点数量，当到达这个数量时停止构建新节点。
-
无更多可分特征：所有特征都已经被用于划分，并且当前节点下的样本已经无法通过剩余特征得到更优的划分结果。
