模拟梯度下降法

In [1]:

import numpy as np
import matplotlib.pyplot as plt
import datetime;print ('Run by CYJ,',datetime.datetime.now())

In [2]:

plot_x = np.linspace(-1., 6., 141)
plot_x

Out[2]:

array([-1.  , -0.95, -0.9 , -0.85, -0.8 , -0.75, -0.7 , -0.65, -0.6 ,-0.55, -0.5 , -0.45, -0.4 , -0.35, -0.3 , -0.25, -0.2 , -0.15,-0.1 , -0.05,  0.  ,  0.05,  0.1 ,  0.15,  0.2 ,  0.25,  0.3 ,0.35,  0.4 ,  0.45,  0.5 ,  0.55,  0.6 ,  0.65,  0.7 ,  0.75,0.8 ,  0.85,  0.9 ,  0.95,  1.  ,  1.05,  1.1 ,  1.15,  1.2 ,1.25,  1.3 ,  1.35,  1.4 ,  1.45,  1.5 ,  1.55,  1.6 ,  1.65,1.7 ,  1.75,  1.8 ,  1.85,  1.9 ,  1.95,  2.  ,  2.05,  2.1 ,2.15,  2.2 ,  2.25,  2.3 ,  2.35,  2.4 ,  2.45,  2.5 ,  2.55,2.6 ,  2.65,  2.7 ,  2.75,  2.8 ,  2.85,  2.9 ,  2.95,  3.  ,3.05,  3.1 ,  3.15,  3.2 ,  3.25,  3.3 ,  3.35,  3.4 ,  3.45,3.5 ,  3.55,  3.6 ,  3.65,  3.7 ,  3.75,  3.8 ,  3.85,  3.9 ,3.95,  4.  ,  4.05,  4.1 ,  4.15,  4.2 ,  4.25,  4.3 ,  4.35,4.4 ,  4.45,  4.5 ,  4.55,  4.6 ,  4.65,  4.7 ,  4.75,  4.8 ,4.85,  4.9 ,  4.95,  5.  ,  5.05,  5.1 ,  5.15,  5.2 ,  5.25,5.3 ,  5.35,  5.4 ,  5.45,  5.5 ,  5.55,  5.6 ,  5.65,  5.7 ,5.75,  5.8 ,  5.85,  5.9 ,  5.95,  6.  ])

In [3]:

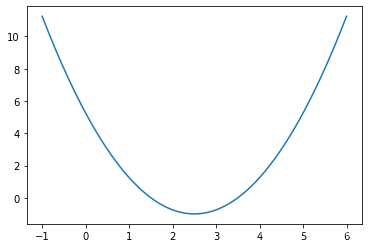
plot_y = (plot_x-2.5)**2 - 1.

In [4]:

plt.plot(plot_x, plot_y)
plt.show()

In [5]:

epsilon = 1e-8
eta = 0.1

In [6]:

def J(theta):return (theta-2.5)**2 - 1.def dJ(theta):return 2*(theta-2.5)theta = 0.0
while True:gradient = dJ(theta)last_theta = thetatheta = theta - eta * gradientif(abs(J(theta) - J(last_theta)) < epsilon):breakprint(theta)
print(J(theta))

2.499891109642585
-0.99999998814289

In [7]:

theta = 0.0
theta_history = [theta]
while True:gradient = dJ(theta)last_theta = thetatheta = theta - eta * gradienttheta_history.append(theta)if(abs(J(theta) - J(last_theta)) < epsilon):breakplt.plot(plot_x, J(plot_x))
plt.plot(np.array(theta_history), J(np.array(theta_history)), color="r", marker='+')
plt.show()

In [8]:

len(theta_history)

Out[8]:

46

In [9]:

theta_history = []def gradient_descent(initial_theta, eta, epsilon=1e-8):theta = initial_thetatheta_history.append(initial_theta)while True:gradient = dJ(theta)last_theta = thetatheta = theta - eta * gradienttheta_history.append(theta)if(abs(J(theta) - J(last_theta)) < epsilon):breakdef plot_theta_history():plt.plot(plot_x, J(plot_x))plt.plot(np.array(theta_history), J(np.array(theta_history)), color="r", marker='+')plt.show()

In [10]:

eta = 0.01
theta_history = []
gradient_descent(0, eta)
plot_theta_history()

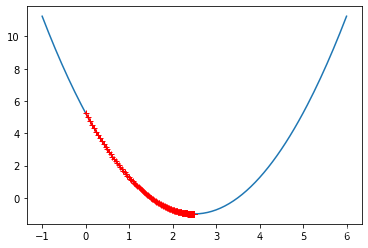
In [11]:

len(theta_history)

Out[11]:

424

In [12]:

eta = 0.001
theta_history = []
gradient_descent(0, eta)
plot_theta_history()

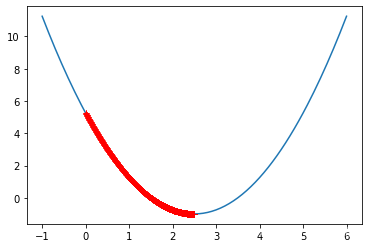
In [13]:

len(theta_history)

Out[13]:

3682

In [14]:

eta = 0.8
theta_history = []
gradient_descent(0, eta)
plot_theta_history()

In [16]:

eta = 1.1
theta_history = []
gradient_descent(0, eta)

---------------------------------------------------------------------------
OverflowError                             Traceback (most recent call last)
<ipython-input-16-89c87a003181> in <module>1 eta = 1.12 theta_history = []
----> 3 gradient_descent(0, eta)<ipython-input-9-46124331ca03> in gradient_descent(initial_theta, eta, epsilon)11         theta_history.append(theta)12 
---> 13         if(abs(J(theta) - J(last_theta)) < epsilon):14             break15 <ipython-input-6-09073b555d68> in J(theta)1 def J(theta):
----> 2     return (theta-2.5)**2 - 1.3 4 def dJ(theta):5     return 2*(theta-2.5)OverflowError: (34, 'Result too large')

In [17]:

def J(theta):try:return (theta-2.5)**2 - 1.except:return float('inf')

In [18]:

def gradient_descent(initial_theta, eta, n_iters = 1e4, epsilon=1e-8):theta = initial_thetai_iter = 0theta_history.append(initial_theta)while i_iter < n_iters:gradient = dJ(theta)last_theta = thetatheta = theta - eta * gradienttheta_history.append(theta)if(abs(J(theta) - J(last_theta)) < epsilon):breaki_iter += 1return

In [19]:

eta = 1.1
theta_history = []
gradient_descent(0, eta)

In [20]:

len(theta_history)

Out[20]:

10001

In [21]:

eta = 1.1
theta_history = []
gradient_descent(0, eta, n_iters=10)
plot_theta_history()

In [ ]:

In [ ]: