数据预处理|数据清洗|使用Pandas进行异常值清洗
- 使用Pandas进行异常值清洗
- 1. 异常值检测
- 1.1 简单统计分析
- 1.2 散点图方法
- 1.3 3σ原则
- 1.4 箱线图
- 2. 异常值处理
- 2.1 直接删除
- 2.2 视为缺失值
- 2.3 平均值修正
- 2.4 盖帽法
- 2.5 分箱平滑法
- 2.6 回归插补
- 2.7 多重插补
- 2.8 不处理
使用Pandas进行异常值清洗
异常值是指那些在数据集中存在的不合理的值,这里所说不合理的值是偏离正常范围的值,不是错误值。异常值的存在会严重干扰数据分析的结果。
1. 异常值检测
1.1 简单统计分析
最常用的统计量是最大值和最小值,用来判断这个变量的取值是否超出合理的范围。如电商信息表中客户年龄age=199,则该变量的取值存在异常。
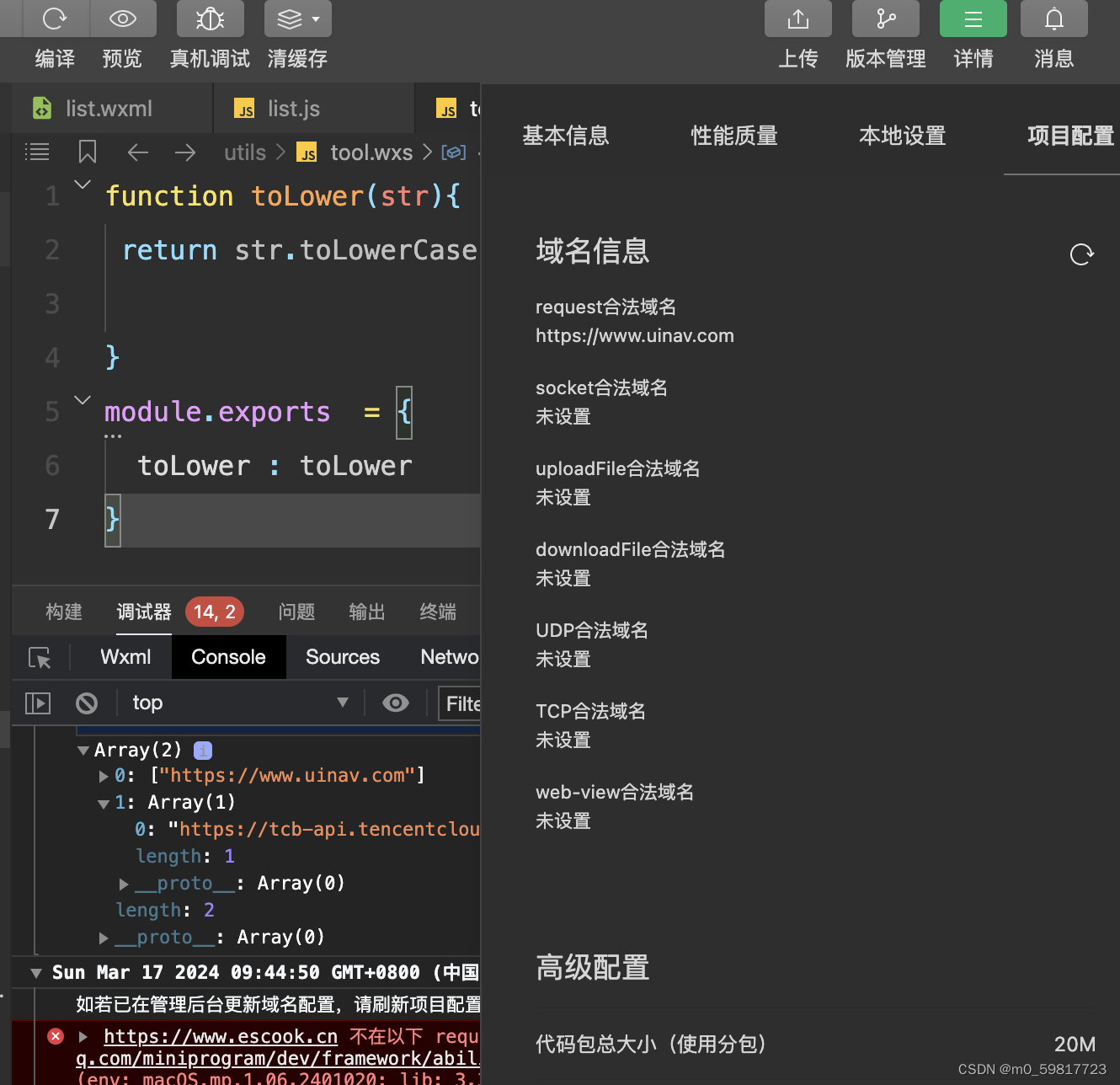
- 例1. 计算成年人的身高、体重公式为:Y=(X-100)×1.2,其中X为身高(cm),Y为标准体重(kg)。
import matplotlib.pyplot as plt
import numpy as np
#假设成年人(18岁以上)正常高度在1.4米至2.0米
x=np.arange(140,200,5)
y=(x-100)*1.2
plt.rcParams['font.family']='STSong' #图形中显示汉字
plt.rcParams['font.size']=10
plt.title('身高和体重')
plt.plot(x,y,'.')
plt.plot(150,187,'r.') #异常值
plt.plot(166,212,'r.') #异常值
plt.plot(187,208,'r.')
plt.show()
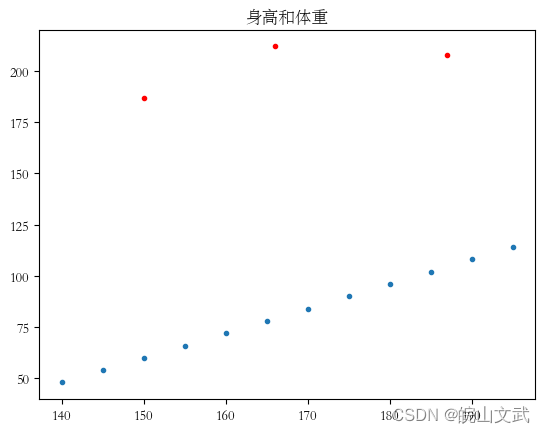
1.2 散点图方法
通过数据分布的散点图可以检测异常数据。
- 例2. 分析房屋面积和房屋价格的关系示例。
import matplotlib.pyplot as plt
import numpy as np
x = [225.98,247.07,253.14,254.85,241.58,301.01,20.67,288.64, 163.56,120.06,207.83,342.75,147.9,53.06,224.72,29.51,21.61,483.21, 245.25,299.25,343.35] #房屋面积数据
y = [196.63,203.88,210.75,372.74,202.41,347.61,24.9,239.34, 140.32,304.15,176.84,488.23,128.79,49.64,191.74,33.1,30.74,400.02,205.35,330.64,283.45] #房屋价格数据
plt.figure(figsize=(6, 5), dpi=100) #创建画布
plt.scatter(x, y,s=40) # 绘制散点图
plt.show() # 显示图像
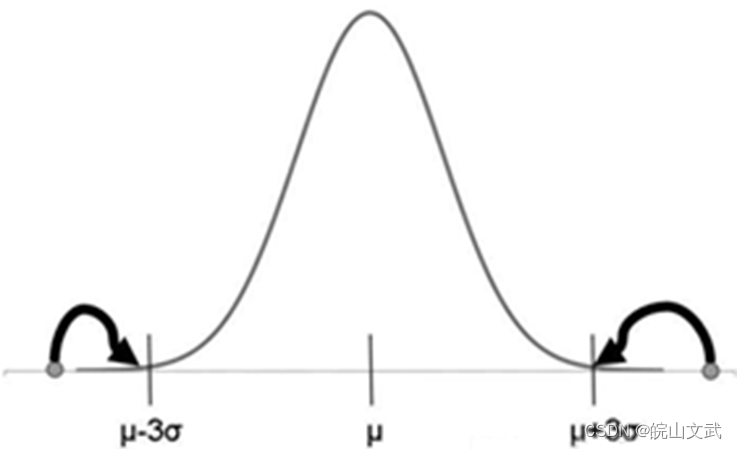
1.3 3σ原则
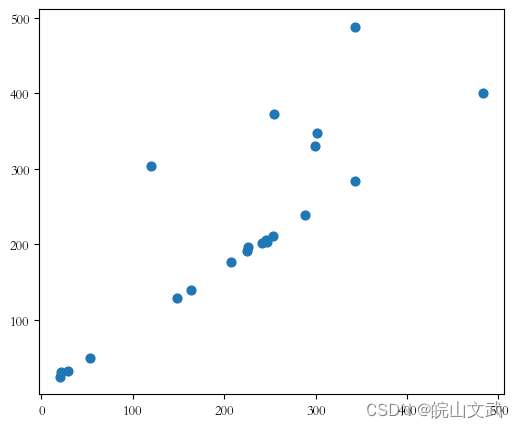
在正态分布中, σ \sigma σ代表标准差, μ \mu μ代表均值, x = μ x=\mu x=μ即为图像的对称轴。
3 σ 3\sigma 3σ原则认为:数值分布在 ( μ − σ , μ + σ ) (\mu - \sigma , \mu + \sigma ) (μ−σ,μ+σ)中的概率为0.6827;数值分布在 ( μ − 2 σ , μ + 2 σ ) (\mu - 2\sigma , \mu + 2\sigma ) (μ−2σ,μ+2σ)中的概率为0.9544;数值分布在 ( μ − 3 σ , μ + 3 σ ) (\mu - 3\sigma , \mu + 3\sigma ) (μ−3σ,μ+3σ)中的概率为0.9974。也就是说,Y 的取值几乎全部集中在 ( μ − 3 σ , μ + 3 σ ) (\mu - 3\sigma , \mu + 3\sigma ) (μ−3σ,μ+3σ)区间内,超出这个范围的可能性仅占不到0.3%,属于极个别的小概率事件,因此将超出 ( μ − 3 σ , μ + 3 σ ) (\mu - 3\sigma , \mu + 3\sigma ) (μ−3σ,μ+3σ)范围的值都可以认为是异常值,如下图所示。
3σ原则要求数据服从正态或近似正态分布,且样本数量大于10。
- 例3. 3σ原则检测异常值示例。
import pandas as pd
data=[199,78,72,70,68,72,77,78,42,78,74,54,80,82,65,62,60] #学生某门课程成绩
s=pd.Series(data)
dmean=s.mean()
dstd=s.std()
print('\n检测出异常值:')
yz1=dmean-3*dstd
yz2=dmean+3*dstd
for i in range(0,len(data)):if (data[i]<yz1)or(data[i]>yz2):print(data[i],end=',')
检测出异常值:
199,
1.4 箱线图
箱线图是通过数据集的四分位数形成的图形化描述,是非常简单而且有效的可视化异常值的一种检测方法。
- 例4. 箱线图检测异常值示例。
import pandas as pd
import matplotlib.pyplot as plt
data=[78,72,32,70,68,72,77,78,56,78,74,54,80,82,65,62]
s=pd.Series(data)
plt.boxplot(x=s.values,whis=1.5)
plt.show()
#从图中可以看出,检测出的异常值为32。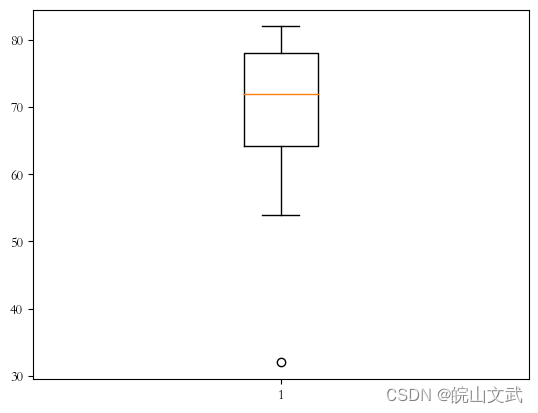
2. 异常值处理
异常值处理是数据预处理中的一个重要步骤,它是保证原始数据可靠性,平均值与标准差计算准确性的前提。
2.1 直接删除
直接将含有异常值的记录删除。这种方法简单易行,但缺点也不容忽视,一是在观测值很少的情况下,这种删除操作会造成样本量不足;二是直接删除、可能会对变量的原有分布造成影响,从而导致统计模型的不稳定。
2.2 视为缺失值
利用处理缺失值的方法来处理。这一方法的好处是能够利用现有变量的信息,来填补异常值。需要注意的是,将该异常值作为缺失值处理,需要根据该异常值的特点来进行,此时需要考虑该异常值(缺失值)是完全随机缺失、随机缺失还是非随机缺失的不同情况进行不同处理。
2.3 平均值修正
如果数据的样本量很小的话,也可用前后两个观测值的平均值来修正该异常值。这其实是一种比较折中的方法,大部分的参数方法是针对均值来建模的,用平均值来修正,优点是能克服丢失样本的缺陷,缺点是丢失了样本“特色”。
2.4 盖帽法
将某连续变量均值上下三倍标准差范围外的记录替换为均值上下三倍标准差值,即盖帽处理。如下图所示。
2.5 分箱平滑法
分箱平滑法是指通过考察“邻居”(周围的值)来平滑存储数据的值。分箱的主要目的是消除异常值,将连续数据离散化,增加粒度。
- 分箱
在分箱前,一定要先排序数据,再将它们分配到等深(等宽)的箱子中。
等深分箱:按记录数进行分箱,每箱具有相同的记录数,每箱的记录数称为箱子的权重,也称箱子的深度。
等宽分箱:在整个属性值的区间上平均分布,即每个箱的区间范围设定为一个常量,称为箱子的宽度。
例如客户收入属性income排序后的值(人民币:元):2300,2500, 2800,3000,3500,4000,4500,4800,5000,5300,5500,6000,6200,6700,7000,7200,分箱的结果如下:
等深分箱。如深度为4,分箱结果为:
箱1:2300,2500,2800,3000;
箱2:3500,4000,4500,4800;
箱3: 5000,5300,5500,6000;
箱4:6200,6700,7000,7200。
等宽分箱。如宽度为1200元人民币,分箱结果为:
箱1:2300,2500,2800,3000,3500;
箱2:4000,4500,4800,5000;
箱3:5300,5500,6000,6200;
箱4: 6700,7000,7800。 - 数据平滑
将数据划分到不同的箱子之后,可以运用如下三种策略对每个箱子中的数据进行平滑处理。
平均值平滑:箱中的每一个值被箱中数值的平均值替换。
中值平滑:箱中的每一个值被箱中数值的中值替换。
边界平滑:箱中的最大值和最小值称为箱子的边界,箱中的每一个值被最近的边界值替换。
2.6 回归插补
对于两个相关变量之间的变化模式,通过回归插补适合一个函数来平滑数据。若是变量之间存在依赖关系,也就是 y = f ( x ) y=f(x) y=f(x),那么就可以设法求出依赖关系 f f f,再根据 x x x来预测 y y y,这也是回归问题的实质。实际问题中更为常见的假设是 p ( y ) = N ( f ( x ) ) p(y)=N(f(x)) p(y)=N(f(x)), N N N为正态分布。假设 y y y是观测值并且存在异常值,求出的 x x x和 y y y之间的依赖关系,再根据 x x x来更新 y y y的值,这样就能去除其中的异常值,这也是回归消除异常值的原理 。
2.7 多重插补
多重插补的处理有两个要点:先删除y变量的缺失值然后插补。需要注意以下两个方面,一是被解释变量有缺失值时不能填补,只能删除;二是只对放入模型的解释变量进行插补。
2.8 不处理
根据该异常值的性质特点,使用更加稳健模型来修饰,然后直接在该数据集上进行数据挖掘。