题意

给定一张 $n$ 个点 $m$ 条边的无向图，对于每个除 $1$ 以外的点 $u$，求在不允许经过原来从 $1$ 到 $u$ 的最短路径的最后一条边时，$1$ 到 $u$ 的最短路。

保证 $1$ 到其他点的最短路唯一，无解输出 -1。

解法

如果每次暴力删边后再跑一次最短路复杂度显然不行。题目中给了最短路唯一的条件，可以建出最短路径树，把每条从 $1$ 到其他所有点的最短路径上的边拎出来单独建一棵树。

对于一条最短路径上的最后一条边 $(u,v)$（$u$ 为 $v$ 的祖先），我们删去它后会导致树上 $1$ 与 $v$ 不连通（最短路径唯一），意味着需要走至少一条非树边。

推理可知：新的最短路只会经过一条非树边。假设需要经过两条及以上的非树边，那么总是有至少一条非树边可以用几条树边拼起来（否则这条非树边就应当是树边）。可以脑补一下走多条非树边的情况，一定存在一个更优的只走一条非树边的路径。

所以，从 $1$ 到 $v$ 的新最短路径可以用一条非树边连接两条树上路径组成。不妨枚举每一条非树边对新最短路径的贡献。

对于一条非树边 $(u,v)$，记 $u,v$ 的最近公共祖先为 $lca$，如果将其加进最短路树中，则会产生一个环，环上的点为 $u\to lca$ 和 $v\to lca$ 两条链上的点。那么 $(u,v)$ 可能可以更新的点即为这个环上除了 $lca$ 的其他点（对 $u$ 和 $v$ 也能够产生贡献）。

• 如果一个点 $x$ 在这个环上，且不是 $lca$，那么断开它和其父亲的这条边后，就可以以另一个方向绕这个环（比如说一开始要从 $lca$ 往 $u$ 的方向走，那么这次就往 $v$ 的方向走，然后再走 $(u,v)$ 这条边，从 $u$ 往上爬爬到 $x$），途中只会经过 $(u,v)$ 这一条非树边。
• 如果一个点 $x$ 是 $lca$ 及其祖先，那么断开这么一条边后从 $1$ 甚至无法到达这个环，再多花一条非树边走到环上不如另找一个非树边，走另一个环，回到第一种情况。
• 如果一个点 $x$ 是 $u$ 或 $v$ 的后代，那么断开这条边后也无法到达环上，与情况二相同，不如另找一个环。

此时，如果点 $x$ 满足条件并打算走 $(u,v)$ 这条边，设 $1\to a$ 的最短路（即树上路径长度）为 $di{s}_a$，则新的 $1\to x$ 的路径长度为 $di{s}_u+w(u,v)+di{s}_v-di{s}_i$，其中 $w(u,v)$ 为 $(u,v)$ 的边权。建议看图理解。

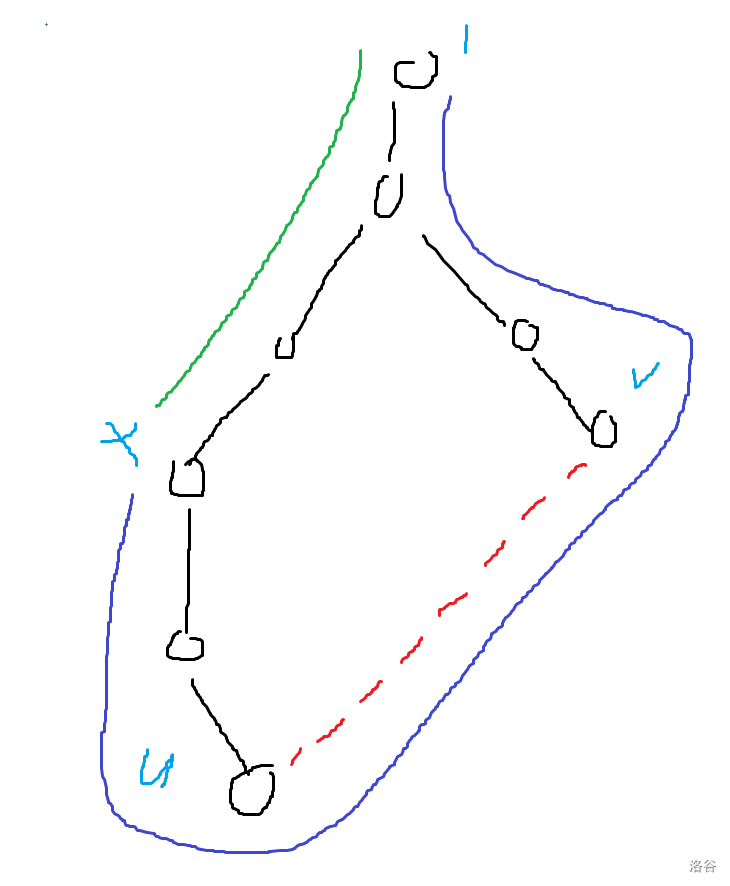
• 把 $u$ 和 $v$​ 的位置反过来是同理的。

$di{s}_i$ 是不变的，所以我们把每条边按照 $di{s}_u+w(u,v)+di{s}_v$ 从小到大进行排序，每次遍历一遍环上没有被确定答案的点并更新答案，这样可以保证每个点被最优的非树边计算答案，不会重复计算。

实现

用 Dijkstra 算出最短路，根据松弛操作 $di{s}_v\leftarrow \min (di{s}_v,di{s}_u+w(u,v))$，只需在算法结束后遍历每条边 $(u,v)$，判断 $di{s}_v$ 是否与 $di{s}_u+w(u,v)$ 相等，如果是则说明有一条最短路经过了 $(u,v)$，$(u,v)$ 即为最短路树树边。

跳过已经确定答案的点考虑使用并查集缩点。在环上的点的答案被更新以后，我们把它们全部归到一个并查集里，根节点为 $lca$ 或者它的祖先。在遍历另一个环时，如果环上某一段被更新完了，则直接用并查集往上跳到环上下一个没被更新过的点。

复杂度不太会分析所以就是 O(能过) 因为每个点的答案只会被计算一次，否则会被跳过，复杂度应该就是 $O(m\log m)$​ 的（对非树边进行排序）。

个人认为这个并查集更像是记录每个点最近的没被计算过贡献的祖先，加快了在环上跳的过程；而路径压缩的过程就是把跳的好几下压缩成跳一下就到。

代码

// Dijkstra构建最短路径树
// 按照dis[u]+w[u][v]+dis[v]排序
// 最后并查集缩点（类似Kruskal）
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn = 2e5 + 5;
struct Edge { int u,v; ll w; int nxt;Edge(int a = 0,int b = 0,ll c = 0,int d = 0) { u = a, v = b, w = c, nxt = d; }
} e[maxn << 1];
int head[maxn],cnt,n;
void addEdge(int u,int v,ll w) {e[++ cnt] = Edge(u,v,w,head[u]);head[u] = cnt;
}
ll dis[maxn]; bool vis[maxn]; int tot;
pair<ll,pair<int,int> > newEdge[maxn << 1];
vector<int> mp[maxn];
void Dijkstra() {#define type pair<ll,int>priority_queue<type,vector<type>,greater<type> > q;for (int i = 2;i <= n;i ++) dis[i] = 2e18;q.push({0,1}); dis[1] = 0;while (!q.empty()) {int u = q.top().second; q.pop();if (vis[u]) continue; vis[u] = true;for (int i = head[u];i;i = e[i].nxt) {int v = e[i].v; ll w = e[i].w;if (dis[v] > dis[u] + w) {dis[v] = dis[u] + w;if (!vis[v]) q.push({dis[v], v});}}}// 选出非树边for (int i = 1;i <= cnt;i ++) {int u = e[i].u, v = e[i].v, w = e[i].w;if (dis[v] != dis[u] + w && u <= v)newEdge[++ tot] = {dis[u] + dis[v] + w, {u, v}};else if (dis[v] == dis[u] + w) mp[u].push_back(v);}#undef type
}
int dep[maxn],fat[maxn]; // 算深度和每个点的父亲。
void dfs(int u,int fa) {dep[u] = dep[fat[u] = fa] + 1;for (auto v : mp[u])if (v != fa) dfs(v,u);
}
int m,fa[maxn]; ll ans[maxn];
int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
int main() {scanf("%d%d",&n,&m); ll w;for (int i = 1,u,v;i <= m;i ++) {scanf("%d%d%lld",&u,&v,&w);addEdge(u,v,w); addEdge(v,u,w);}Dijkstra(); dfs(1,0);sort(newEdge + 1,newEdge + tot + 1);for (int i = 1;i <= n;i ++)ans[i] = -1, fa[i] = i;// 算答案for (int i = 1;i <= tot;i ++) {int u = find(newEdge[i].second.first); // 直接找到一个最近的没被计算过答案的点。int v = find(newEdge[i].second.second);ll w = newEdge[i].first;while (u != v) { // 当u,v相等时说明跳到了lca及以上，不在环上了。if (dep[u] < dep[v]) u ^= v, v ^= u, u ^= v; // 每次把u,v中深度较大的点往上挪。ans[u] = w - dis[u], fa[u] = fat[u]; // 可以往上跳但还在环上，那么自己被计算过了，下一个没被计算过的点就是fa[fat[u]]。u = find(u); // 往上跳，注意有路径压缩。}}for (int i = 2;i <= n;i ++)printf("%lld\n",ans[i]);return 0;
}
// 记得开long long！