目录
906.区间问题--区间分组
906.区间问题--区间分组
原题:
给定 N 个闭区间 [ai,bi],请你将这些区间分成若干组,使得每组内部的区间两两之间(包括端点)没有交集,并使得组数尽可能小。
输出最小组数。
输入格式
第一行包含整数 N,表示区间数。
接下来 N 行,每行包含两个整数 ai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示最小组数。
数据范围
1≤N≤105,
−109≤ai≤bi≤109输入样例:
3 -1 1 2 4 3 5输出样例:
2
难度:简单 时/空限制:1s / 64MB 总通过数:27839 总尝试数:57884 来源: 模板题
算法标签
先上代码:
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
const int N=1e5+10;struct Range{int l,r;bool operator < (const Range &w)const//运算符重载{return l<w.l;//按照区间左端点从小到大排序}
}range[N];int main()
{int n;cin>>n;for(int i=0;i<n;i++) cin>>range[i].l>>range[i].r;sort(range,range+n);//是定义一个小根堆的优先队列,并按照从小到大的顺序排列,即最小的元素位于小根堆的顶端,较大的数放在较下的位置 priority_queue<int,vector<int>,greater<int> > heap;for(int i=0;i<n;i++){//如果已存在的组的右端点>=r.l则说明有交集,则要开新组if(heap.empty()||heap.top()>=range[i].l) heap.push(range[i].r);//否则就放到最小值那个组里面去,更新栈顶。这样可以使得所分的组最少,这里体现了贪心的思想。else{heap.pop();heap.push(range[i].r);}}cout<<heap.size();return 0;
} 思路:
通过举例来解释,设现有已经排好序的6个区间,如下图所示 。①~⑭为代码中for循环的过程,画了☆的表示这一步是在排序(每次有变化小根堆就会自动排序,将最小的值放到顶部,较大的值往下放,注意:堆只能访问根节点,其余结点无法操作)。
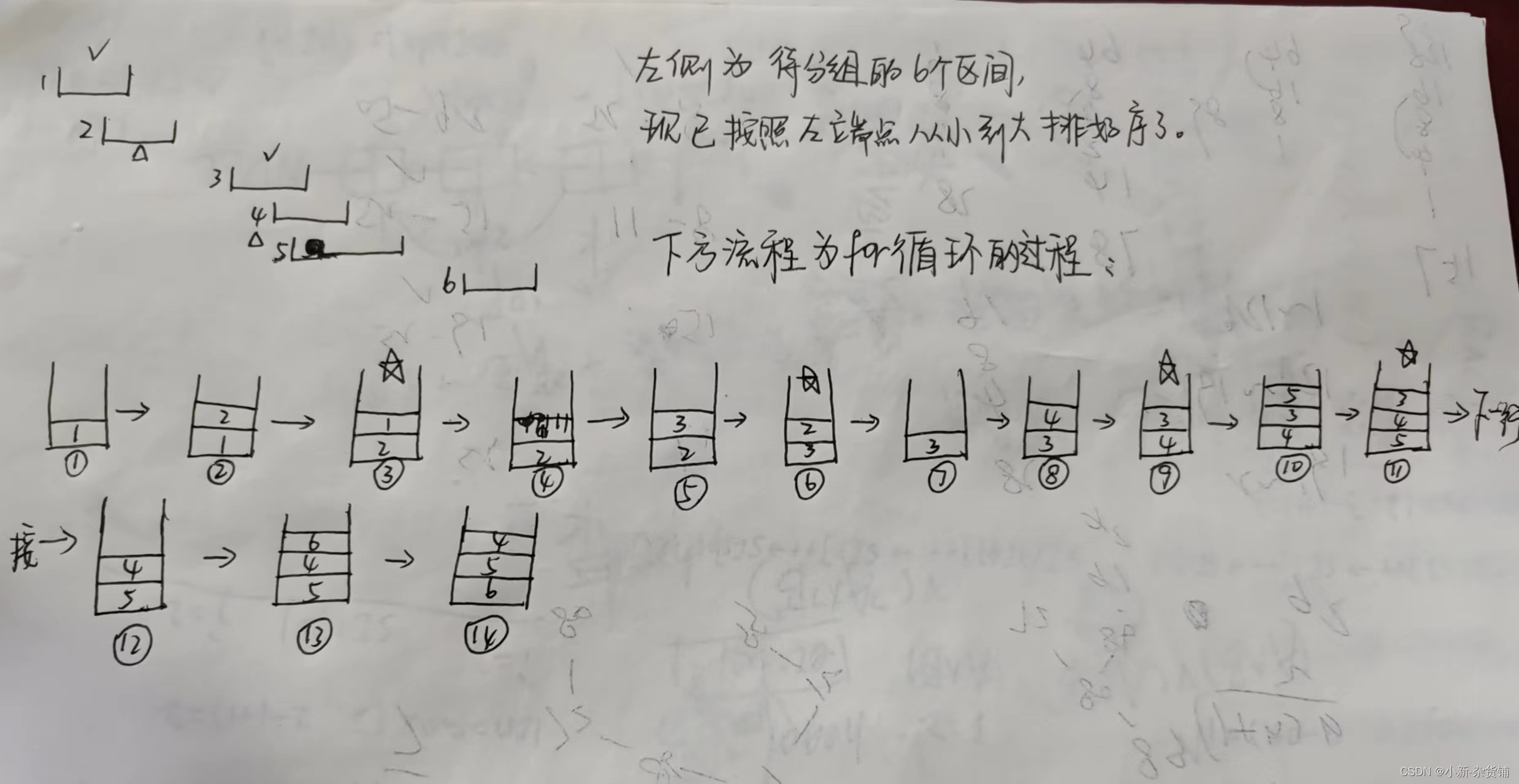
①:将区间1压入;(ps:压入的都是区间的右端点)
②:区间1的右端点大于区间2的左端点,说明两区间有交集,需要重新开一个组,将区间2压入;
③:小根堆内部排序,将区间1的右端点放在顶端,区间2往下放;
④:区间3的左端点大于区间1的右端点,将区间1弹出;
⑤:再将区间3压入;
⑥:小根堆排序;
⑦:区间4的左端点大于区间2的右端点,将区间2弹出;
⑧:再将区间4压入;
⑨:小根堆排序;
⑩:区间3的右端点大于区间5的左端点,说明两区间有交集,需要重新开一个组,将区间5压入;
⑪:小根堆排序;
⑫:区间6的左端点大于区间3的右端点,将区间3弹出;
⑬:再将区间6压入;
⑭:小根堆排序。
最后分组的结果是:
区间 1,3,6 为一组,区间 2,4 为一组,区间 5 为一组,共3组。