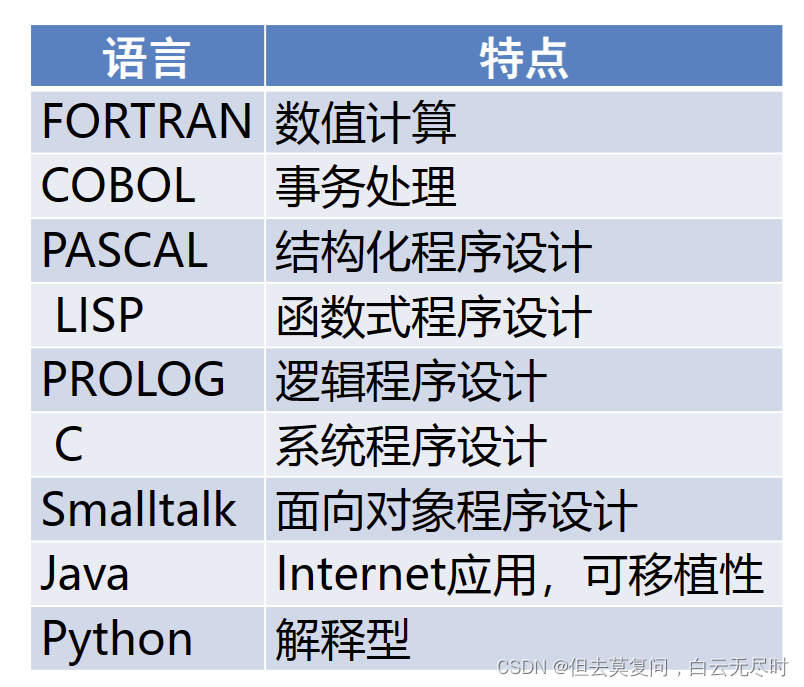
常用的高级程序设计语言

程序语言的定义

语法

一组规则，用它可以形成和产生合适的程序

词法规则：单词符号的形成规则。

单词符号的形成规则单词符号是语言中具有独立意义的最基本结构

一般包括:常数、标识符、基本字、算符、界符等

描述工具:有限自动机

语法规则：语法单位的形成规则。
语法单位通常包括:表达式、语句、分程序、过程函数、程序等；
描述工具:上下文无关文法

 

语义

一组规则，用它可以定义一个程序的意义

描述方法
        自然语言描述
                二义性、隐藏错误和不完整性
        形式描述
                操作语义
                指称语义
                代数语义

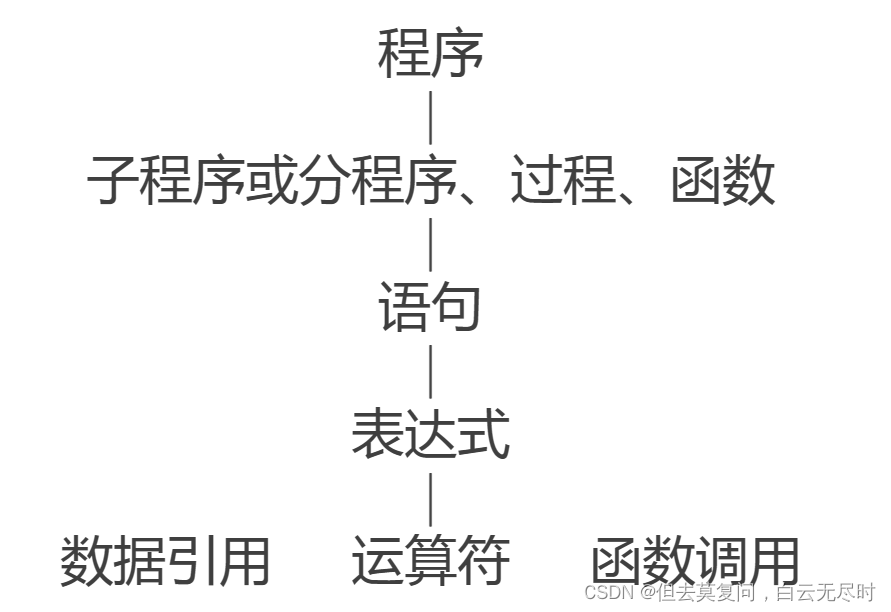
程序的层次结构

 

高级程序语言的一般特性

高级语言的分类

强制式语言(lmperative Languge)/过程式语言

        命令驱动、面向语句

        FORTRAN、C、Pascal， Ada

应用式语言(Applicative Language)

        注重程序所表示的功能，而不是一个语句接一个语句地执行
        LISP、ML

基于规则的语言( Rule-based Language)

        检查一定的条件，当它满足值，则执行适当的动作
        Prolog

面向对象语言(Object-Oriented Language)

        封装、继承和多态性
        Smalltalk，C++,Java

程序语言的语法基础

文法和语言

文法：描述语言的语法结构的形式规则

语言描述的几个基本概念：

字母表：一个有穷字符集，记为∑

字母表中每个元素称为字符 ∑上的字(也叫字符串)  是指由∑中的字符所构成的一个有穷序列

不包含任何字符的序列称为空字，记为ε

用∑*表示∑上的所有字的全体，包含空字ε

        例如: 设 ∑={a， b}，则

        ∑*={ε,a,b,aa,ab,ba,bb,aaa,...}

∑*的子集U和V的连接（积）定义为

UV＝{ab | aU & bV }

示例：设 U＝{ a, aa } V＝ { b, bb }       

         UV={ ab, abb, aab, aabb}

V自身的 n次积记为     Vn=V V…V(n个)

V={ε}

V*是V的闭包： V*=V0∪V1∪V2∪V3∪…

V+是V的正规闭包：V＋＝V V* 

规则（产生式） 是一有序对<u,x>,通常写作u->x。 

上下文无关文法

上下文无关文法G是一个四元组          

        G=(VT，VN，S，P)，其中

VT：终结符(Terminal)集合(非空)

VN：非终结符(Noterminal)集合(非空)，且VT  VN=

S：文法的开始符号，SVN

P：产生式集合(有限)，每个产生式形式为 P->a， PVN， a (VT  VN)*

开始符S至少必须在某个产生式的左部出现一次

 

 

推导

直接推导

​​​​​​​ 

间接推导

 

最左推导和最右推导 

句子句型语言

​​​​​​​​​​​​​​

句子是特殊句型

例题

 

 

 

语法分析树和二义性

语法树

文法是二义的

一个文法某个句子存在两颗对应的不同语法树

语言的二义性

二义性问题是不可判断问题，即不存在一个算法，它能在有限步骤内，确切地判定一个文法是否是二义的

形式语言鸟瞰

乔姆斯基于1956年建立形式语言体系，他把文法分成四种类型：0，1，2，3型

 

 

 

 

 

上下文有关&&上下文无关

一、上下文无关文法
上下文无关文法就是说这个文法中所有的产生式左边只有一个非终结符，比如：

S -> aSb
S -> ab

这个文法有两个产生式，每个产生式左边只有一个非终结符 S，这就是上下文无关文法，因为你只要找到符合产生式右边的串，就可以把它归约为对应的非终结符。

二、上下文有关文法
比如：

aSb -> aaSbb
S -> ab

这就是上下文有关文法，因为它的第一个产生式左边有不止一个符号，所以你在匹配这个产生式中的S的时候必需确保这个S有正确的“上下文”，也就是左边的a和右边的b，所以叫上下文相关文法。

原文链接：https://blog.csdn.net/weixin_44636558/article/details/107188377