java数据结构与算法刷题目录（剑指Offer、LeetCode、ACM）-----主目录-----持续更新(进不去说明我没写完)：https://blog.csdn.net/grd_java/article/details/123063846

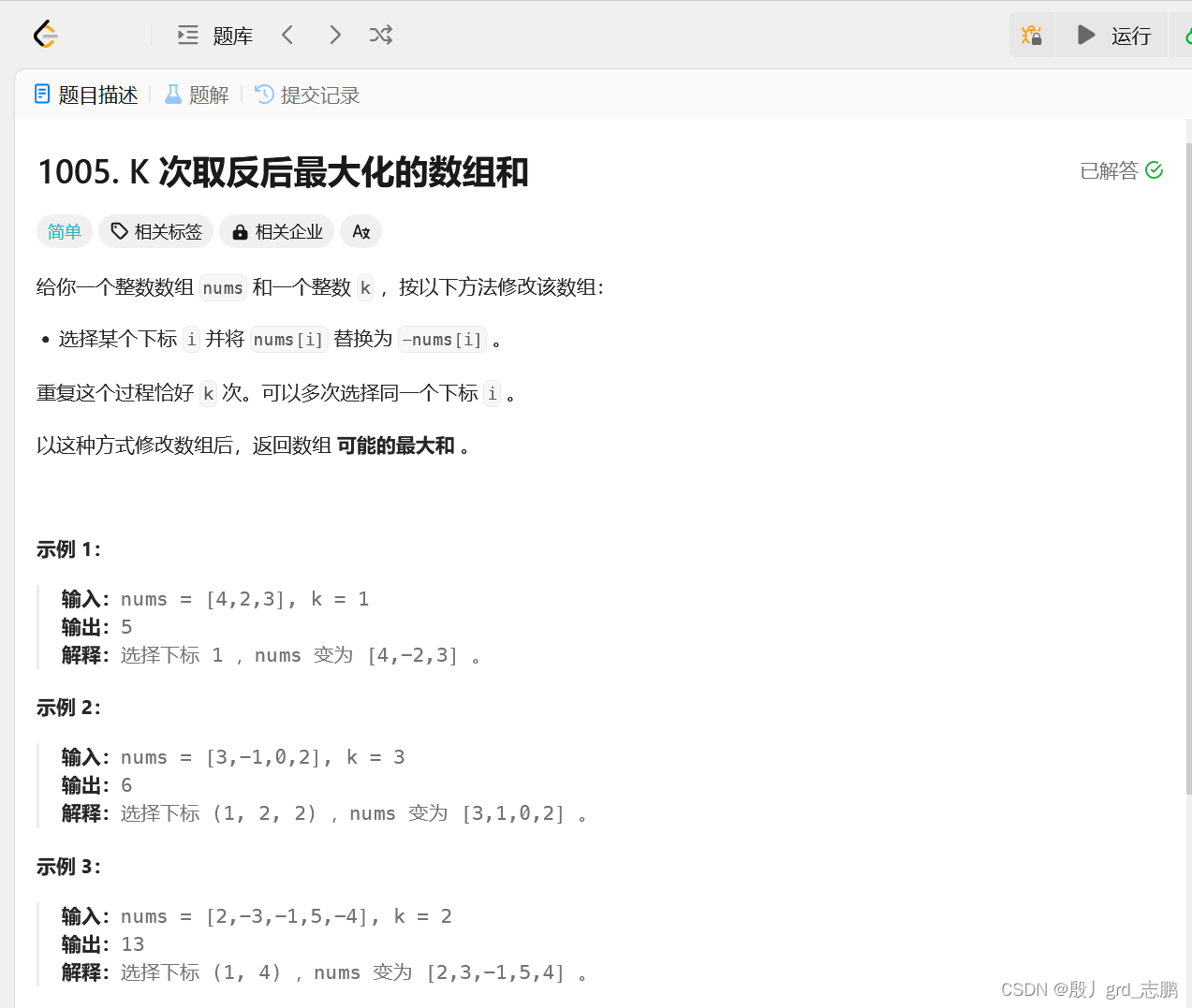
卷来卷去，把简单题都卷成中等题了

1. 排序后从小到大取负

解题思路：时间复杂度O($n\ast lo{g}_{2}n$),时间复杂度的大头就是排序算法. 空间复杂度O($lo{g}_{2}n$),快速排序算法需要栈空间

将数组排序后，从小到大取负即可

代码

class Solution {public int largestSumAfterKNegations(int[] nums, int k) {// 排序，把可能有的负数排到前面Arrays.sort(nums);int sum = 0;for (int i = 0; i < nums.length; i++) {// 贪心：如果是负数，而k还有盈余，就把负数反过来if (nums[i] < 0 && k > 0) {nums[i] = -1 * nums[i];k--;}sum += nums[i];}Arrays.sort(nums);// 如果k没剩，那说明能转的负数都转正了，已经是最大和，返回sum// 如果k有剩，说明负数已经全部转正，所以如果k还剩偶数个就自己抵消掉，不用删减，如果k还剩奇数个就减掉2倍最小正数。return sum - (k % 2 == 0 ? 0 : 2 * nums[0]); }
}

2. hash表从小到大排序，省掉排序（这就是为什么这题不是简单题）

上面方法一，排序浪费了大量时间，这个方法，将排序的时间省下来了 , 一举将这道简单题，升为中等难度的题。

解题思路：时间复杂度O($n+c$)，n是数组长度，c是数组中元素的取值范围. 空间复杂度O($C$)

1. 先将数组所有数字放入hash表统计其在数组中出现的次数，并且统计数组的所有元素和sum
2. 然后从小到大依次对hash表中的负数取负（因为是负数，越小，取负后就越大。比如-100 和0 ，明显-100更小，但是取负后，变为100和0,100反而更大）、
3. 共取负k次，取负的过程中，修改sum的值，如何修改呢？这个是个固定套路。

将sum中的某一个负数(-x)改为正数(x)，需要加两倍的x. 例如5 + (-1) = 4 , -1取负后结果为 5 + 1 = 6; ==> 4 + 1*2 = 6。也就是sum + (-x) = newSum, 取负 newSum + 2 * x = newNewSum

4. 此时如果所有负数都取负完成，k依然没有归0，说明我们还需要继续取负。此时剩余的数字都是正数，所以我们对最小的数字取负即可。有以下两种情况

1. 剩余k为偶数，因为-(-1) = 1.也就是对一个正数x取负偶数次，结果依然是x
2. 剩余k为奇数，因为奇数-1为偶数。也就是我们对正数x先取负偶数次，结果依然是x次，然后再对其取负1次即可。简单来说，对剩余数字中最小的取负一次，然后对sum处理即可
3. 注意：对一个sum中的一个正数取负，需要减去两个它。注意和上面将sum中一个负数取负区分。

代码

1. 使用数组充当hash表的效率
   
2. 使用HashMap的效率（所以不使用这种方法,从而将这道题的难度又提升了一些）
   

代码中的细节:普通使用hash表的效率很低，所以这道题想要超越100%的用户，需要使用数组充当hash表，这也是为什么这道题不是简单题的原因（新手很难转过来这个弯）

1. 用数组充当hash表，因为题目所给取值范围为[-100 , 100]，所以我们需要一个大小为201的数组充当hash表。也可以直接用HashMap（但是对于做题来说，效率就慢了）
2. hash数组下标从0开始，则下标0代表-100.下标1代表-99，…，下标100代表0,…,下标200代表100
3. 对于一个数字i来说，需要+100才是hash数组中对应的位置，因为-100+100 = 0，正好存在hash[0]的位置
4. 既然hash[100]代表数字0，那么hash[100] 保存正数 hash[200]
5. 对于一个负数来说，对其取负后，他变为正数，应该存放到hash[200-i]的位置，例如-100取负为100，-100原本在hash[0],则 i = 0. 此时变成正数后，应该存放到hash[200]. 也就是hash[200-(0)] ==>hash[200]

class Solution {public int largestSumAfterKNegations(int[] nums, int k) {int[] arr = new int[201];//hash表，这道题的范围是-100到100，正好需要201个位置存储。下标0表示-100int sum = 0;//保存当前nums数组的和for(int n : nums){arr[n+100]++;//统计元素出现次数sum += n;//统计当前所有元素的和}for(int i = 0; i < 100 && k > 0; i++){//从小到大遍历hash表中的负数if(arr[i] != 0){//如果当前数字还有剩余//如果当前数字i出现次数 < k ,则获取i的出现次数//如果当前数字i的出现次数 > k, 则获取k，表示剩余可以取负的次数int min = Math.min(arr[i],k);//获取当前数字的出现次数和k，较小的一个k -= min;//对当前数字i，每一个都取负，k表示可取负的次数，需要对min个i取负//负数取负后，变为正数，i = 0表示的是-100，取负变为100，应该存储在i = 200的位置，//i = 200表示的是正100arr[200-i] += min;//对min个i取负，则变为min个正i。存放到相应位置//5 + (-1) = 4 , 5 + 1 = 6; ==> 4 + 1*2 = 6 //sum + (-x) = newSum, 取负 newSum + 2 * x = newNewSum//当一个和的结果中，将一个负数取负后，需要加上两个它哦//我们这里只将负数转为正数，例如将i（0<=i<100）转为正数，是200-i//但是因为sum中取负某个负数i后，需要加上两个i，因此是200-2*i//我们一共取负了min个i，故需要(200-2*i) * minsum += (200-2*i)*min;}}//如果所有负数全部取负后，k还是没有归0，也就是我们必须继续对数字取负//因为k剩偶数个时，我们对同一个取负，结果不变，例如x取负两次，-（-x） = x//如果k还剩奇数个，就需要对某个数继续取负一次，因为 奇数 减去 1 为偶数，偶数次取负，原值不变，则剩一次需要取负if(k % 2 != 0){for(int i = 100; i <= 200; i++){//因为没有负数了，则对现存最小的数字取反一次即可if(arr[i] != 0){//如果当前数字存在sum -= (i-100)*2;//对其取负，对一个sum中的一个正数取负，需要减去两个它return sum;//返回最终结果}}}return sum;//如果在负数全部取负之前（正好全取负完）k就归0了，直接返回sum即可}
}