一 从零实现线性回归
1.1 生成训练数据
原始 计算公式,
我们先使用该公式生成一批数据,然后使用 结果数据去计算 计算 w1, w2 和 b。
%matplotlib inline
import random
import torch
from d2l import torch as d2ldef synthetic_data(w, b, num_examples): #@save"""生成y=Xw+b+噪声"""X = torch.normal(0, 1, (num_examples, len(w)))y = torch.matmul(X, w) + by += torch.normal(0, 0.01, y.shape)return X, y.reshape((-1, 1))
true_w = torch.tensor([2, -3.4])
true_b = 4.2
X, y = synthetic_data(true_w, true_b, 1000)print(f'X:{X[:2, :]}') # 2 * 1.1020 - 3.4 * 1.0722 + 4.2 = 2.758 y1:2.76
print(f'y: {y[:2]}')
# X:tensor([[ 1.1020, 1.0722],
# [ 1.0747, -1.3082]])
# y: tensor([[ 2.7678],
# [10.7949]])可以看到 结果值y 是 使用 数据 计算得到的。
1.2 数据拆分
将数据输入 数据生成器 中,将数据按批次进行拆分,不要一次全部输入模型中,每次输入10个数据,当我们运行迭代时,我们会连续地获得不同的小批量,直至遍历完整个数据集,在深度学习框架中实现的内置迭代器效率要高得多,它可以处理存储在文件中的 数据和数据流提供的数据。:
def data_iter(batch_size, features, labels):num_examples = len(features)indices = list(range(num_examples))# 这些样本是随机读取的,没有特定的顺序random.shuffle(indices)for i in range(0, num_examples, batch_size):batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])yield features[batch_indices], labels[batch_indices]
查看数据拆分示例:
batch_size = 10
for feature, label in data_iter(batch_size, X, y):print(feature, '\n', label)break
1.3 初始化模型参数
随机初始化 特征权重w1, w2, b, 随机给个初始值才可以让它不断去靠近我们的实际权重值,从均值为0、标准差为0.01的正态分布中采样随机数来初始化权重,并将 偏置初始化为0。:
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
w, b# (tensor([[-0.0119],
# [ 0.0133]], requires_grad=True),
# tensor([0.], requires_grad=True))1.4 定义模型
用于前向传播的 模型,通过该模型计算预测值,要计算线性模型的输 出,我们只需计算输入特征X和模型权重w的矩阵‐向量乘法后加上偏置b:
def linreg(X, w, b): #@save"""线性回归模型"""return torch.matmul(X, w) + b # 用于计算两个张量(tensor)的矩阵乘法。1.5 定义损失函数
本次使用 平方损失 作为损失函数:
def squared_loss(y_hat, y): #@save"""均方损失"""return (y_hat - y.reshape(y_hat.shape)) ** 2 / 21.6 定义优化算法
使用 随机梯度下降作为优化算法,在每一步中,使用从数据集中随机抽取的一个小批量,然后根据参数计算损失的梯度:
def sgd(params, lr, batch_size): #@save # param:w1, w2, b"""小批量随机梯度下降"""with torch.no_grad():for param in params:param -= lr * param.grad / batch_sizeparam.grad.zero_()1.7 执行训练
查看执行训练的过程,学习率为每次 移动的步长,batch_size 为每次训练输出的数据量,num_epochs 为训练迭代过程:
1 计算每次的损失值。
2 反向传播计算梯度,就是计算权重实时的导数。
3 根据实时的梯度更新权重值。
lr = 0.01 # 学习率
batch_size = 100 # 每次训练数据输出数据量
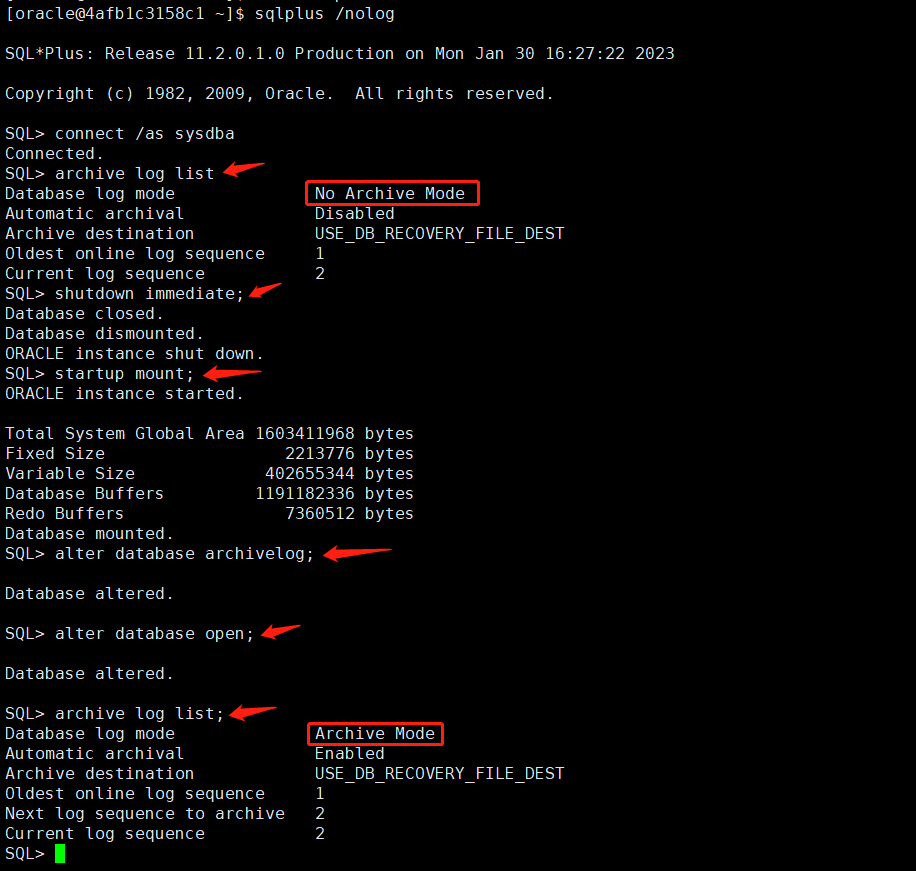
num_epochs = 1000 # 训练次数for epoch in range(num_epochs):for feature, label in data_iter(batch_size, X, y):l = squared_loss(linreg(feature, w, b), label) # 计算损失print(f'epoch:{epoch:3}, [w, b]: [{w[0].item():.5f},{w[1].item():.5f},{b.item():.5f}], loss:{l.mean():.5f}')l.sum().backward() # 反向传播计算 w,b 的实时梯度sgd([w, b], lr, batch_size) # 更新w,b原始公式:

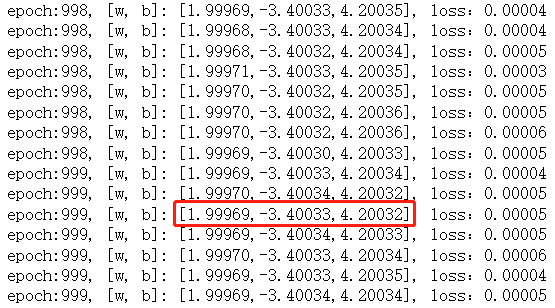
可以看出 训练到后期,w1,w2,b的值和原始生成数据的公式基本吻合。
二 简洁实现线性回归(调包)
数据集生成:
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2ltrue_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)def load_array(data_arrays, batch_size, is_train=True): #@save"""构造一个PyTorch数据迭代器"""dataset = data.TensorDataset(*data_arrays)return data.DataLoader(dataset, batch_size, shuffle=is_train)batch_size = 10
data_iter = load_array((features, labels), batch_size)查看下数据,注意这里数据加载使用了 load_array:
next(iter(data_iter))
a 定义模型
# nn是神经网络的缩写
from torch import nn
net = nn.Sequential(nn.Linear(2, 1))
net
# Sequential(
# (0): Linear(in_features=2, out_features=1, bias=True)
# )b 初始化权重
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
# tensor([0.])c 定义损失函数
loss = nn.MSELoss()d 定义优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.03)
trainer
f 执行训练
num_epochs = 3
for epoch in range(num_epochs):for X, y in data_iter:l = loss(net(X) ,y)trainer.zero_grad() # 用于将模型中所有参数的梯度清零。l.backward()trainer.step()l = loss(net(features), labels)print(f'epoch {epoch + 1}, loss {l:f}')
查看计算的最后结果:
w = net[0].weight.data
print(f'w: {w.reshape(true_w.shape)},w误差:', true_w-w.reshape(true_w.shape))
b = net[0].bias.data
print(f'b: {b.item():.5f}, b的误差:', true_b - b)# w: tensor([ 2.0003, -3.3999]),w误差: tensor([-3.0398e-04, -7.4625e-05])
# b: 4.19952, b的误差: tensor([0.0005])原始公式:
三 线性回归 其他相关知识
线性模型的四个模块:训练数据,线性模型,损失函数,优化算法。
a. 数据集
使用房价预测数据集,我们希望根据房屋的面积和房龄等来估算房屋价格。
b. 线性模型
预测公式, 价格 = 权重1 * 面积 + 权重2 * 房龄 + 截距:
![]()
c. 损失函数
拟合最小二乘法,使用平方误差:
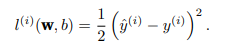
在训练模型时,我们希望寻找一组参数(w∗ , b∗),这组参数能 最小化在所有训练样本上的总损失 。
线性回归的解可以用一个公式简单地表达出来,这类解叫作解析解(analytical solution)。
d. 优化算法
梯度下降最简单的用法是 计算损失函数(数据集中所有样本的损失均值)关于模型参数的导数(在这里也可 以称为梯度)。但实际中的执行可能会非常慢:因为在每一次更新参数之前,我们必须遍历整个数据集。因此, 我们通常会在 每次需要计算更新的时候随机抽取一小批样本,这种变体叫做小批量随机梯度下降(minibatch stochastic gradient descent)。
给定特征估计目标的过程通常称为预测(prediction)或推断(inference)。
3.1 矢量化加速
定义计时器,用来 查看算法运行时间:
%matplotlib inline
import mathimport time
import numpy as np
import torch
from d2l import torch as d2lclass Timer: #@save"""记录多次运行时间"""def __init__(self):self.times = []self.start()def start(self):"""启动计时器"""self.tik = time.time()def stop(self):"""停止计时器并将时间记录在列表中"""self.times.append(time.time() - self.tik)return self.times[-1]def avg(self):"""返回平均时间"""return sum(self.times) / len(self.times)def sum(self):"""返回时间总和"""return sum(self.times)def cumsum(self):"""返回累计时间"""return np.array(self.times).cumsum().tolist()查看 for 循环时长:
n = 100000
a = torch.ones([n])
b = torch.ones([n])c = torch.zeros(n) # 初始化
timer = Timer()
for i in range(n):c[i] = a[i] + b[i]
print(f'{timer.stop():.5f} 秒') # 0.51397 秒查看 直接计算 时长:
timer.start()
d = a + b
print(f'{timer.stop():.5f} 秒') # 0.00100 秒
使用向量计算,本次计算优化了 500倍。for 循环画了0.5 秒,而直接计算 只花了 0.001秒!!!
3.2 正态分布
查看 不同均值和方差的正态分布 情况:
def normal(x, mu, sigma):p = 1 / math.sqrt(2 * math.pi * sigma**2)return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)# 再次使用numpy进行可视化
x = np.arange(-8, 8, 0.01)
# 均值和标准差对
params = [(0, 1), (0, 2), (3, 1)]
d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in params], xlabel='x',ylabel='p(x)', figsize=(6, 4),legend=[f'mean {mu}, std {sigma}' for mu, sigma in params])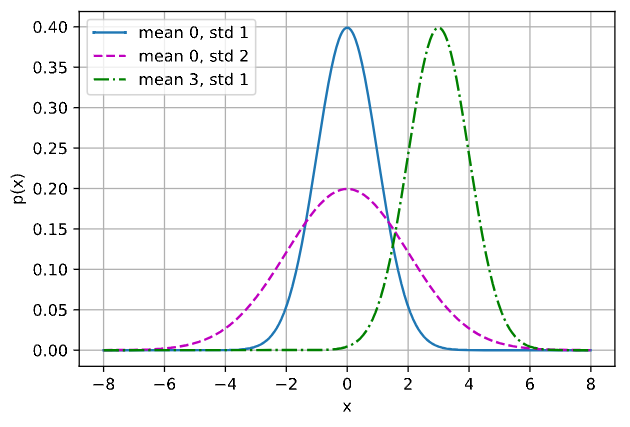
尽管神经网络涵盖了更多更为丰富的模型,我们依然可以用描述神经网络的方式来描述线性模型,从而把 线性模型看作一个神经网络。其实深度神经网络就是成千上万个线性模型组成的一个整体,神经网络里面我们会把输入的每一个特征都去计算一个权重。
对于线性回归,每个输入都与每个输出相连,我们将这种变换称为 全连接层(fully‐connected layer)或称为稠密层(dense layer)。
![[蓝桥杯 2015 省 B] 生命之树](https://img-blog.csdnimg.cn/direct/7bd7daa8c9504bcbaf2b9794db0e8d9d.png)



![[项目设计]基于websocket实现网络对战五子棋](https://img-blog.csdnimg.cn/direct/8cea2f67eb9a44bdb6834b63ca584518.png)