动态规划

• 动态规划：确定好状态方程，我们常常是确定前 当状态来到 i 时，前 i 个物体的状态是怎么样的，我们并不是从一个点去考虑，也就是说虽然我们分割问题，但是问题是相互联系的，那么这就是区别于递归的本质区别

01背包

由于不能拆开，那就是DP 问题，如果能拆开，那就是贪心问题

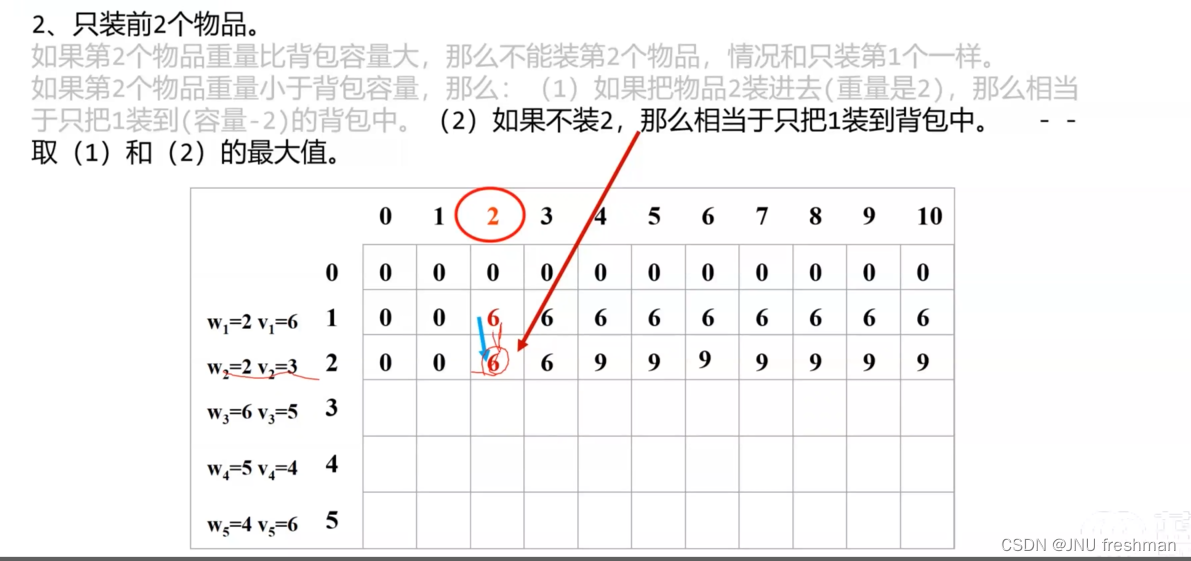
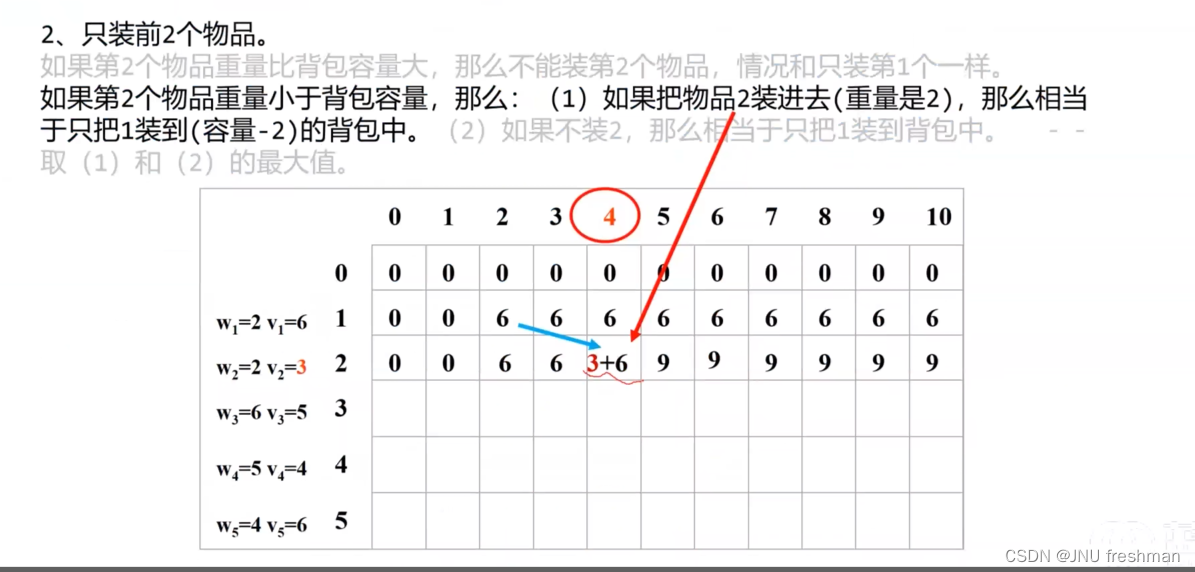
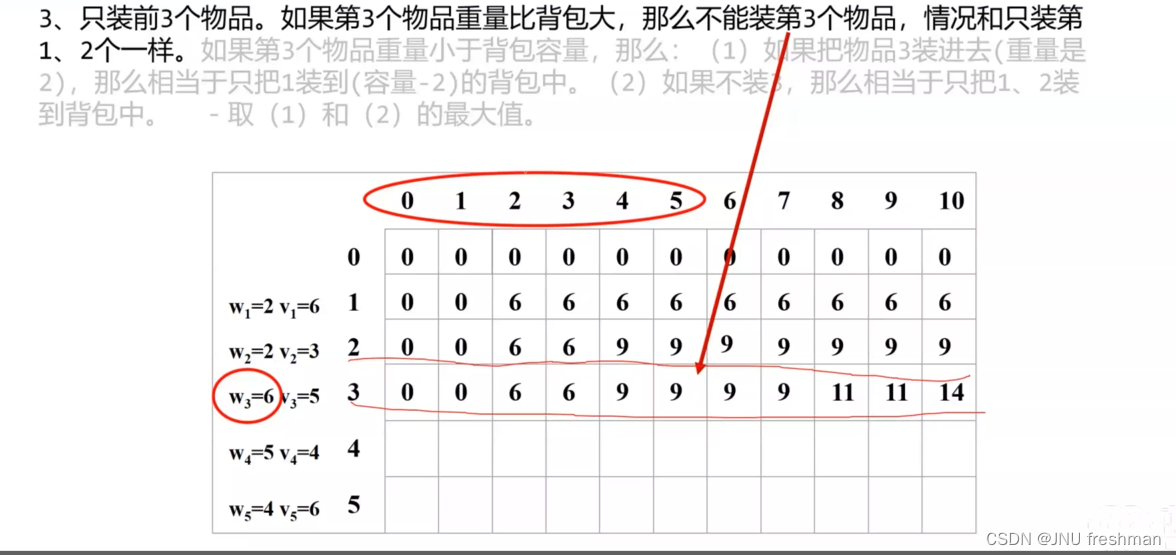
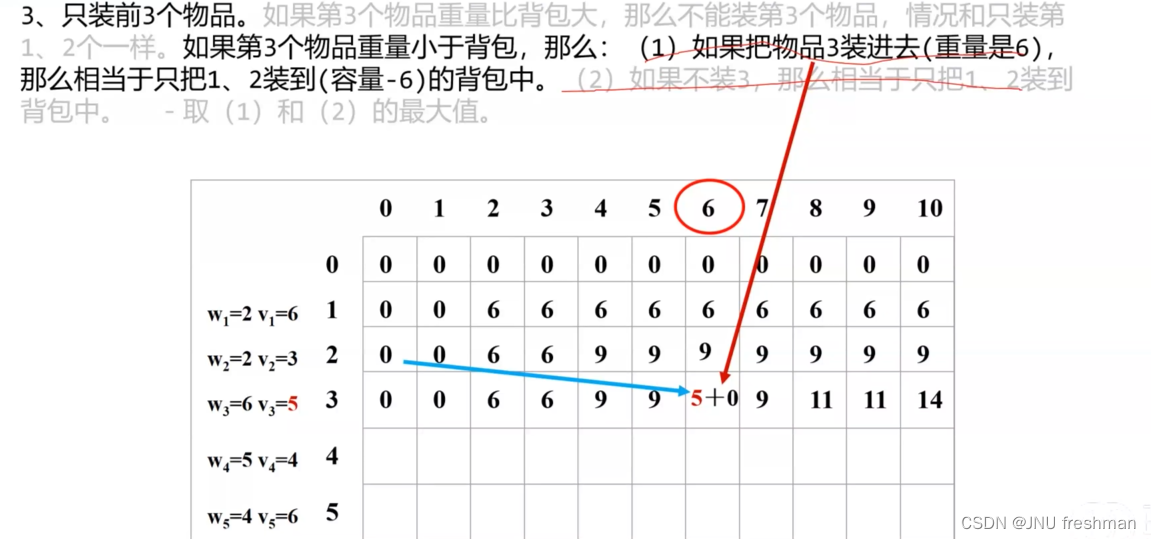
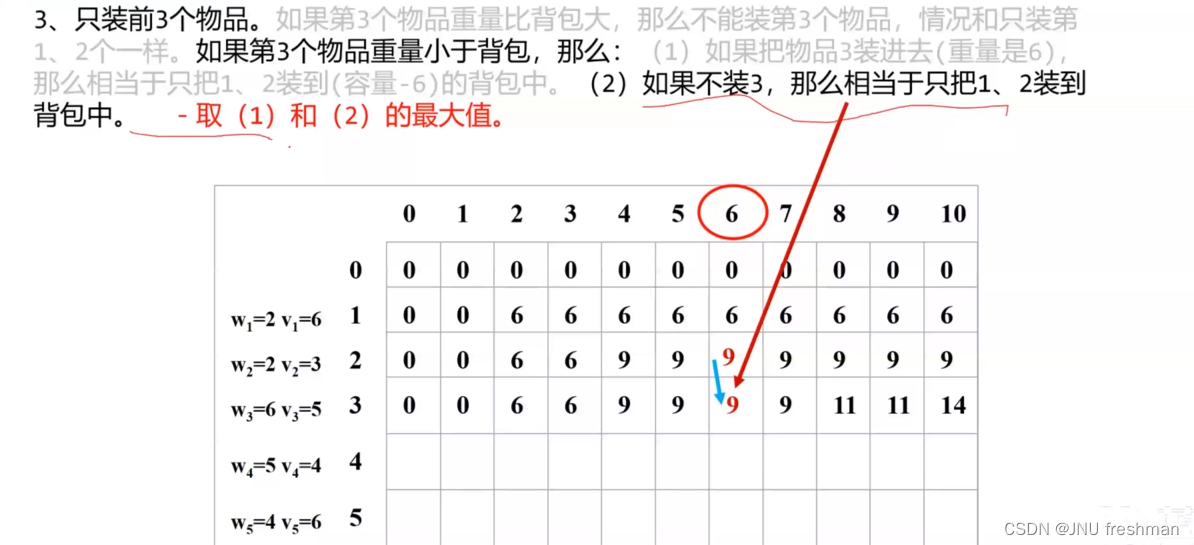
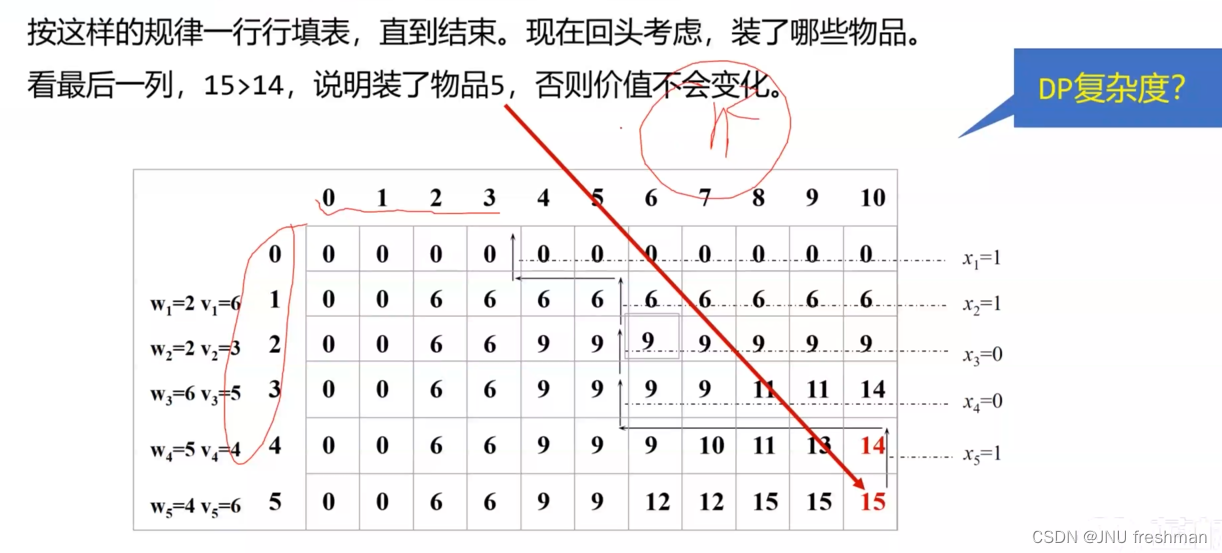
小练一下

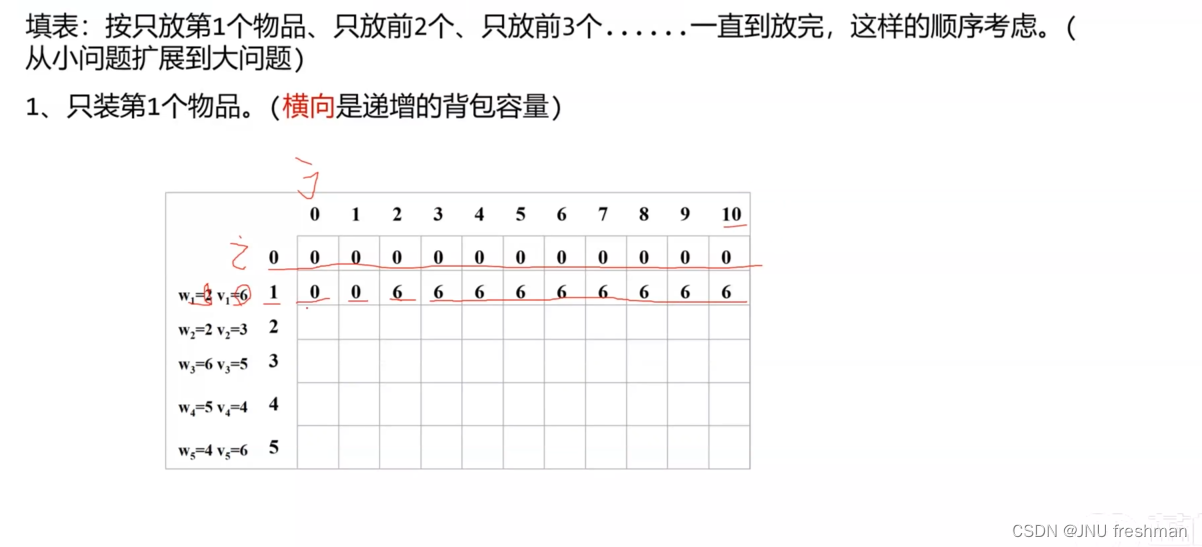
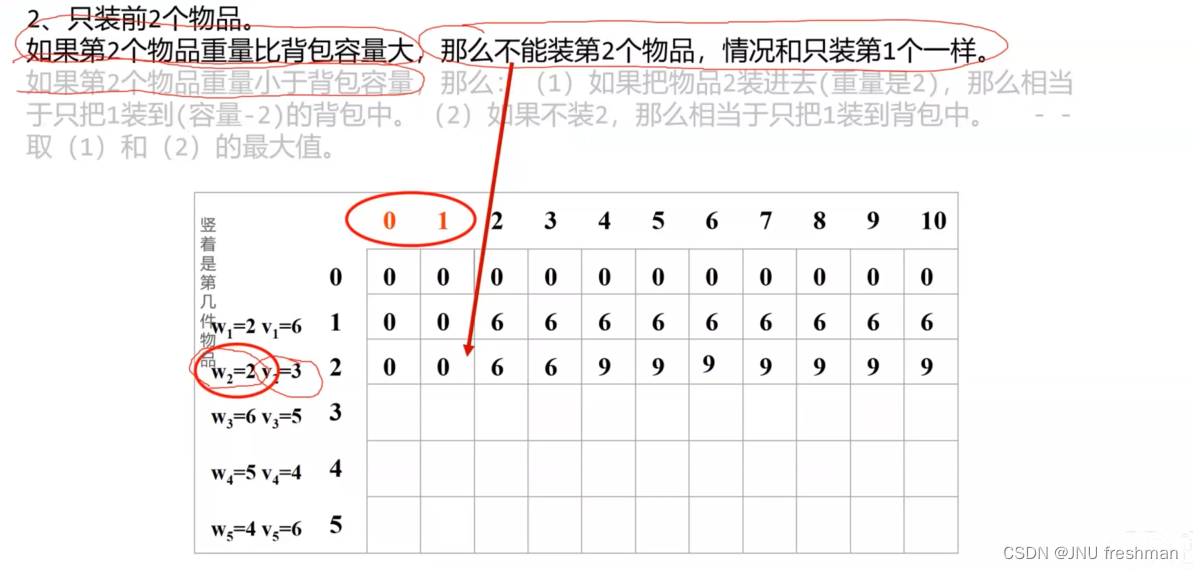
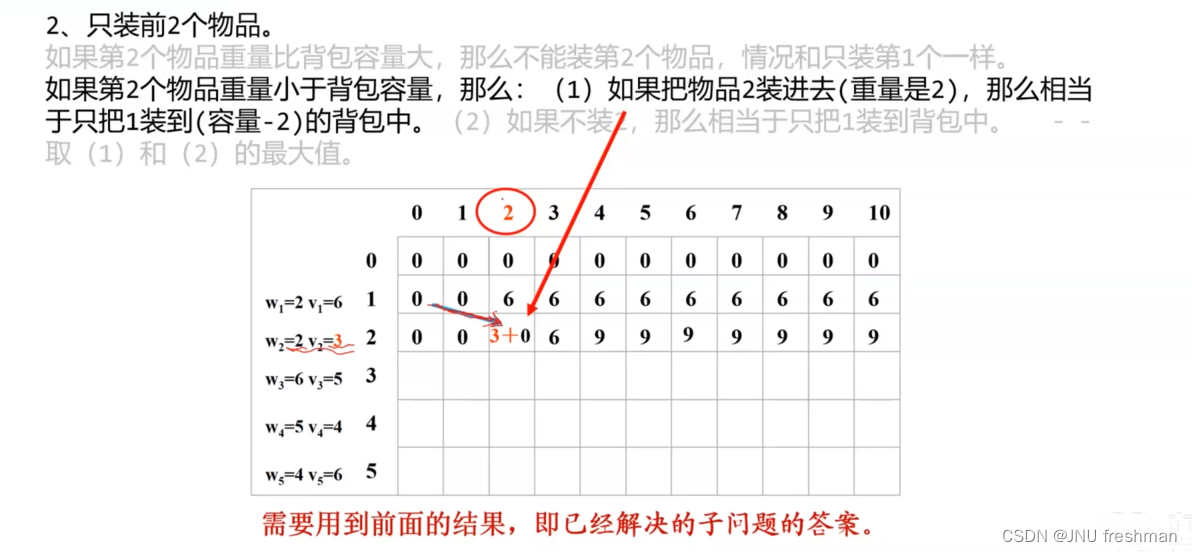
01背包

import os
import sys# 请在此输入您的代码N,V = map(int,input().split())w = []
v = []
w.append(0)
v.append(0)for i in range(N):a,b = map(int,input().split())w.append(a)v.append(b)dp = [[0]*(V+1) for _ in range(N+1)]for i in range(1,N+1):# 取出第i 个物品for j in range(V+1):if j-w[i]<0:dp[i][j]=dp[i-1][j]else:dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])print(dp[N][V])

• 可以对空间进行优化：只用添加两个变量来存储new,old 就是利用滚动数组，两个数组即可解决

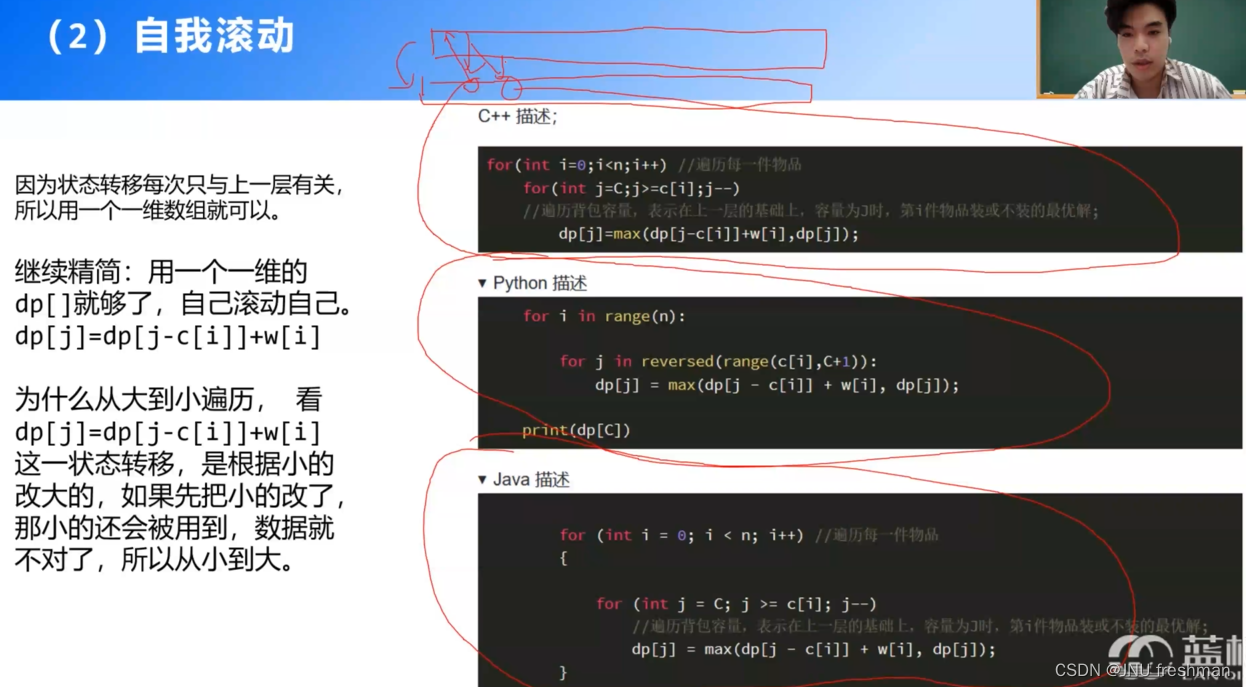
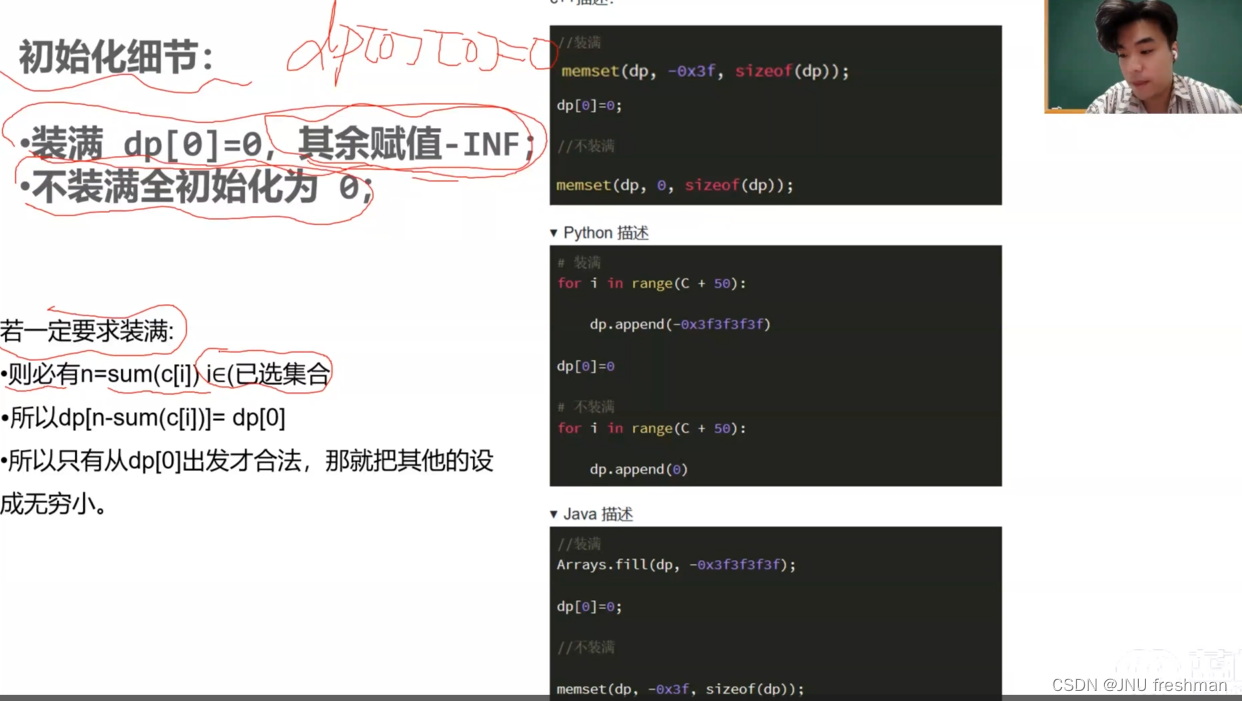
import os
import sysV = int(input())#####箱子容量
n = int(input())####物品数量
l = [0]####各自体积
for i in range(n):####输入体积l.append(int(input()))
dp = [[0 for j in range(V+1)]for i in range(n+1)]for i in range(1,n+1):###for j in range(1,V+1):####if j < l[i]:####dp[i][j] = dp[i-1][j]else:dp[i][j]=max(dp[i-1][j],dp[i-1][j-l[i]]+l[i])###
print(V-dp[n][V])

同样的思路：还是用二维数组存储，dp[i][j]表示 前i 个物体在空间j 的情况下，所能放的空间的大小

网格图上的DP

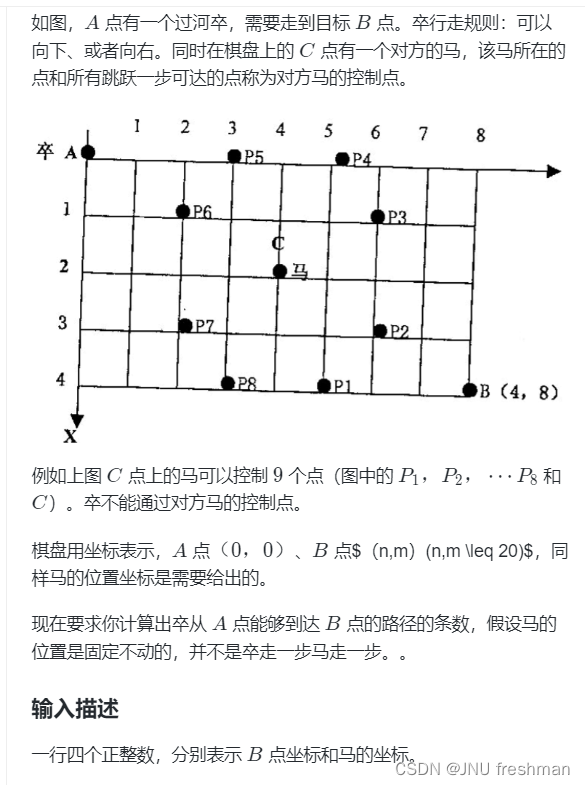
• 对于网格的问题，咋一看好像可以用搜索来解决，但是搜索的话可能就会超时，所以我们可以用动态规划来做，那么如何进行定义？
  dp[i][j] 就是走到(i,j) 的时候的路径数，那么就有 动态规划的式子 ：
  dp[i][j] = dp[i-1][j] + dp[i][j-1] 得来
  对于不能到达的地方，就直接 设置dp 值为0即可
  巧妙地地方：让出发点以及🐎所在地点以及终点都偏移，这样就可以方便解决出界地问题

import os
import sys# 请在此输入您的代码bx, by, mx, my = map(int, input().split())bx += 2
by += 2
mx += 2
my += 2dp = [[0] * (30) for i in range(30)]s = [[False] * 30 for i in range(30)]dp[2][1] = 1
s[mx][my] = Trues[mx - 1][my - 2] = True
s[mx - 1][my + 2] = True
s[mx - 2][my - 1] = True
s[mx - 2][my + 1] = True
s[mx + 1][my - 2] = True
s[mx + 1][my + 2] = True
s[mx + 2][my - 1] = True
s[mx + 2][my + 1] = Truefor i in range(2, bx + 1):for j in range(2, by + 1):if s[i][j]:dp[i][j] = 0else:dp[i][j] = dp[i - 1][j] + dp[i][j - 1]print(dp[bx][by])

完全背包

• 完全背包问题就是在01 背包的基础上，每一件物品是没有个数的限制的，不过可以参照01 背包的思路，因为当第i 种物品的第一件物品就是01 背包问题，后面就是要考虑第 i 件物品
  状态方程
  1.dp[i][j] 表示前 i 种物品，在空间为 j 下能够装下的最大的价值
  2.那么当 pw[i] 第 i 件物品占用的体积大于 j 的时候，那么就只能
  dp[i][j] = dp[i-1][j]
  3.当pw[i] 第 i 件物品占用的体积小于等于 j 的时候，那么就是考虑第i 种物品选不选的问题了，也就是
  dp[i][j] = max(dp[i-1][j] ,dp[i][j-pw[i]]+pv[i])
  其中，dp[i-1][j] 是考虑不选第i 种物品，dp[i][j-pw[i]]+pv[i](01背包的本质区别)是在选了第i 种物品的基础上，再选几件的问题

import os
import sys# 请在此输入您的代码N,V = map(int ,input().split())
pw=[0]
pv=[0]
dp = [[0]*(V+1) for i in range(N+1)]for i in range(N):a,b = map(int,input().split())pw.append(a)pv.append(b)for i in range(1,N+1):for j in range(1,V+1):if j<pw[i]:dp[i][j] = dp[i-1][j]else:dp[i][j] = max(dp[i-1][j],dp[i][j-pw[i]]+pv[i])print(dp[N][V])

最长公共字符串

• 对于这个问题，我们就要考虑从二维方面出发：
  dp[i][j] 表示前i 个 x 的字符 和前 j 个 y 的字符的最长的公共子序列的长度
  1.当x[i]==y[j] 的时候，那么就直接是dp[i][j] = dp[i-1][j-1] +1
  2.不相等的时候，就是dp[i][j] = max(dp[i-1][j],dp[i][j-1])

对于统计数目的话，还在研究：

import os
import sys# 请在此输入您的代码x = input()
y = input()# dp[i][j] 表示 x=xi 与 y=yj 时x与y 的最大的公共子序列的长度
lenx = len(x)
leny = len(y)dp = [[0]*(len(y)) for i in range(len(x))]for i in range(lenx):if x[i]==y[0]:dp[i][0]=1
for i in range(leny):if x[0]==y[i]:dp[0][i]=1for i in range(1,lenx):for j in range(1,leny):if x[i]==y[j]:dp[i][j]=dp[i-1][j-1]+1else:dp[i][j]=max(dp[i-1][j],dp[i][j-1])length =dp[lenx-1][leny-1]
sum=0
for i in range(lenx):for j in range(leny):if dp[i][j]==length:sum = sum +1sum = sum%100000000
print(length)
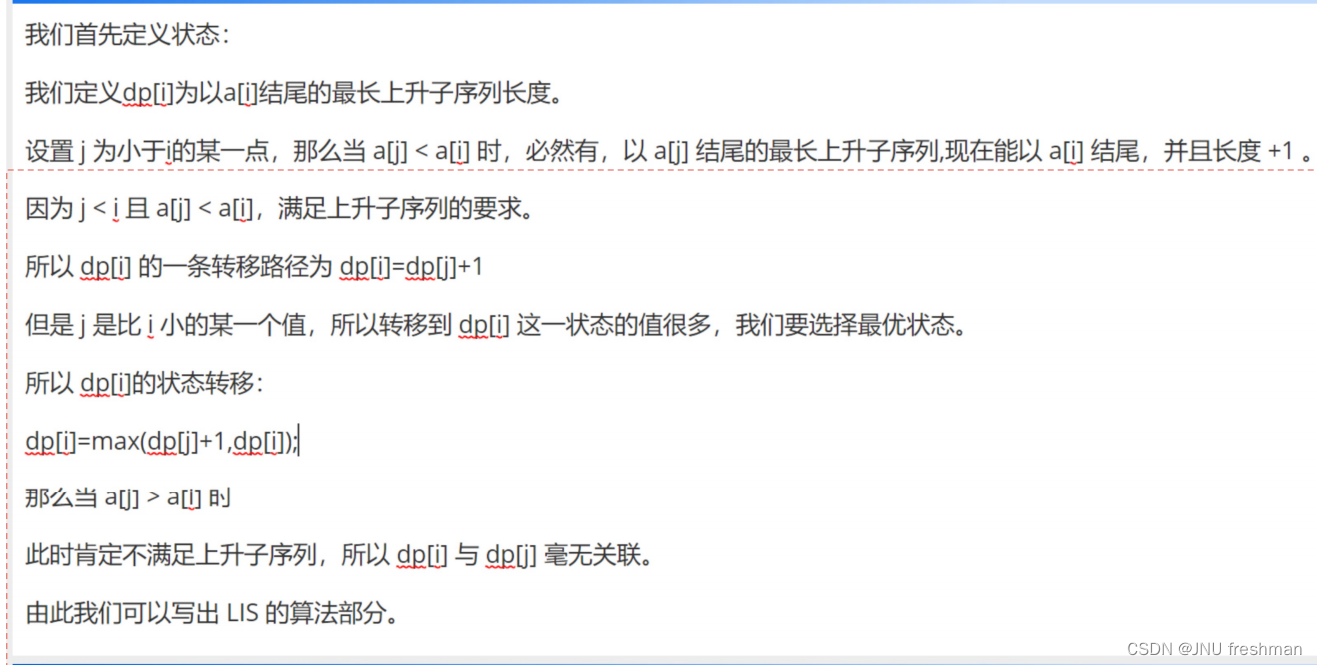
print(sum)

最长递增子序列