四、使用张量表示真实世界数据
本章内容包括
-
将现实世界的数据表示为 PyTorch 张量
-
处理各种数据类型
-
从文件加载数据
-
将数据转换为张量
-
塑造张量,使其可以作为神经网络模型的输入
在上一章中,我们了解到张量是 PyTorch 中数据的构建块。神经网络将张量作为输入,并产生张量作为输出。事实上,神经网络内部的所有操作以及优化过程中的所有操作都是张量之间的操作,神经网络中的所有参数(例如权重和偏置)都是张量。对于成功使用 PyTorch 这样的工具,对张量执行操作并有效地对其进行索引的能力至关重要。现在您已经了解了张量的基础知识,随着您在本书中的学习过程中,您对张量的灵活性将会增长。
现在我们可以回答一个问题:我们如何将一段数据、一个视频或一行文本表示为张量,以便适合训练深度学习模型?这就是我们将在本章学习的内容。我们将重点介绍与本书相关的数据类型,并展示如何将这些数据表示为张量。然后,我们将学习如何从最常见的磁盘格式加载数据,并了解这些数据类型的结构,以便了解如何准备它们用于训练神经网络。通常,我们的原始数据不会完全符合我们想要解决的问题,因此我们将有机会通过一些更有趣的张量操作来练习我们的张量操作技能。
本章的每个部分将描述一种数据类型,并且每种数据类型都将配有自己的数据集。虽然我们已经将本章结构化,使得每种数据类型都建立在前一种数据类型的基础上,但如果你愿意,可以随意跳跃一下。
在本书的其余部分中,我们将使用大量图像和体积数据,因为这些是常见的数据类型,并且在书籍格式中可以很好地再现。我们还将涵盖表格数据、时间序列和文本,因为这些也将引起许多读者的兴趣。因为一图胜千言,我们将从图像数据开始。然后,我们将演示使用代表患者解剖结构的医学数据的三维数组。接下来,我们将处理关于葡萄酒的表格数据,就像我们在电子表格中找到的那样。之后,我们将转向有序表格数据,使用来自自行车共享计划的时间序列数据集。最后,我们将涉足简·奥斯汀的文本数据。文本数据保留了其有序性,但引入了将单词表示为数字数组的问题。
在每个部分中,我们将在深度学习研究人员开始的地方停下来:就在将数据馈送给模型之前。我们鼓励您保留这些数据集;它们将成为我们在下一章开始学习如何训练神经网络模型时的优秀材料。
4.1 处理图像
卷积神经网络的引入彻底改变了计算机视觉(参见 mng.bz/zjMa),基于图像的系统随后获得了全新的能力。以前需要高度调整的算法构建块的复杂流水线现在可以通过使用成对的输入和期望输出示例训练端到端网络以前所未有的性能水平解决。为了参与这场革命,我们需要能够从常见的图像格式中加载图像,然后将数据转换为 PyTorch 期望的方式排列图像各部分的张量表示。
图像被表示为一个规则网格中排列的标量集合,具有高度和宽度(以像素为单位)。 我们可能在每个网格点(像素)上有一个单一的标量,这将被表示为灰度图像;或者在每个网格点上有多个标量,这通常代表不同的颜色,就像我们在上一章中看到的那样,或者不同的 特征,比如来自深度相机的深度。
表示单个像素值的标量通常使用 8 位整数进行编码,如消费级相机。 在医疗、科学和工业应用中,发现更高的数值精度,如 12 位或 16 位,是很常见的。 这允许在像骨密度、温度或深度等物理属性的像素编码信息的情况下拥有更广泛的范围或增加灵敏度。
4.1.1 添加颜色通道
我们之前提到过颜色。 有几种将颜色编码为数字的方法。 最常见的是 RGB,其中颜色由表示红色、绿色和蓝色强度的三个数字定义。 我们可以将颜色通道看作是仅包含所讨论颜色的灰度强度图,类似于如果您戴上一副纯红色太阳镜看到的场景。 图 4.1 展示了一个彩虹,其中每个 RGB 通道捕获光谱的某个部分(该图简化了,省略了将橙色和黄色带表示为红色和绿色组合的内容)。

图 4.1 彩虹,分为红色、绿色和蓝色通道
彩虹的红色带在图像的红色通道中最亮,而蓝色通道既有彩虹的蓝色带又有天空作为高强度。 还要注意,白云在所有三个通道中都是高强度的。
4.1.2 加载图像文件
图像有多种不同的文件格式,但幸运的是在 Python 中有很多加载图像的方法。 让我们从使用 imageio 模块加载 PNG 图像开始(code/p1ch4/1_image_dog.ipynb)。
列表 4.1 code/p1ch4/1_image_dog.ipynb
# In[2]:
import imageioimg_arr = imageio.imread('../data/p1ch4/image-dog/bobby.jpg')
img_arr.shape# Out[2]:
(720, 1280, 3)
注意 我们将在整个章节中使用 imageio,因为它使用统一的 API 处理不同的数据类型。 对于许多目的,使用 TorchVision 处理图像和视频数据是一个很好的默认选择。 我们在这里选择 imageio 进行稍微轻松的探索。
此时,img 是一个类似于 NumPy 数组的对象,具有三个维度:两个空间维度,宽度和高度;以及第三个维度对应于红色、绿色和蓝色通道。 任何输出 NumPy 数组的库都足以获得 PyTorch 张量。 唯一需要注意的是维度的布局。 处理图像数据的 PyTorch 模块要求张量按照 C × H × W 的方式布局:通道、高度和宽度。
4.1.3 更改布局
我们可以使用张量的 permute 方法,使用旧维度替换每个新维度,以获得适当的布局。 给定一个先前获得的输入张量 H × W × C,通过首先将通道 2 放在前面,然后是通道 0 和 1,我们得到一个正确的布局:
# In[3]:
img = torch.from_numpy(img_arr)
out = img.permute(2, 0, 1)
我们之前看到过这个,但请注意,此操作不会复制张量数据。 相反,out 使用与 img 相同的底层存储,并且仅在张量级别上处理大小和步幅信息。 这很方便,因为该操作非常便宜; 但是需要注意的是:更改 img 中的像素将导致 out 中的更改。
还要注意,其他深度学习框架使用不同的布局。 例如,最初 TensorFlow 将通道维度保留在最后,导致 H × W × C 的布局(现在支持多种布局)。 从低级性能的角度来看,这种策略有利有弊,但就我们的问题而言,只要我们正确地重塑张量,就不会有任何区别。
到目前为止,我们描述了单个图像。按照我们之前用于其他数据类型的相同策略,为了创建一个包含多个图像的数据集,以用作神经网络的输入,我们将图像存储在一个批次中,沿着第一个维度获得一个N × C × H × W张量。
作为使用stack构建张量的略微更高效的替代方法,我们可以预先分配一个适当大小的张量,并用从目录加载的图像填充它,如下所示:
# In[4]:
batch_size = 3
batch = torch.zeros(batch_size, 3, 256, 256, dtype=torch.uint8)
这表明我们的批次将由三个 RGB 图像组成,高度为 256 像素,宽度为 256 像素。注意张量的类型:我们期望每种颜色都表示为 8 位整数,就像大多数标准消费级相机的照片格式一样。现在我们可以从输入目录加载所有 PNG 图像并将它们存储在张量中:
# In[5]:
import osdata_dir = '../data/p1ch4/image-cats/'
filenames = [name for name in os.listdir(data_dir)if os.path.splitext(name)[-1] == '.png']
for i, filename in enumerate(filenames):img_arr = imageio.imread(os.path.join(data_dir, filename))img_t = torch.from_numpy(img_arr)img_t = img_t.permute(2, 0, 1)img_t = img_t[:3] # ❶batch[i] = img_t
❶ 这里我们仅保留前三个通道。有时图像还具有表示透明度的 alpha 通道,但我们的网络只需要 RGB 输入。
4.1.4 数据归一化
我们之前提到神经网络通常使用浮点张量作为它们的输入。当输入数据的范围大致从 0 到 1,或从-1 到 1 时,神经网络表现出最佳的训练性能(这是由它们的构建块定义方式所决定的效果)。
因此,我们通常需要做的一件事是将张量转换为浮点数并对像素的值进行归一化。将其转换为浮点数很容易,但归一化则更加棘手,因为它取决于我们决定将输入的哪个范围置于 0 和 1 之间(或-1 和 1 之间)。一种可能性是仅通过 255(8 位无符号数中的最大可表示数)来除以像素的值:
# In[6]:
batch = batch.float()
batch /= 255.0
另一种可能性是计算输入数据的均值和标准差,并对其进行缩放,使输出在每个通道上具有零均值和单位标准差:
# In[7]:
n_channels = batch.shape[1]
for c in range(n_channels):mean = torch.mean(batch[:, c])std = torch.std(batch[:, c])batch[:, c] = (batch[:, c] - mean) / std
注意 这里,我们仅对一批图像进行归一化,因为我们还不知道如何操作整个数据集。在处理图像时,最好提前计算所有训练数据的均值和标准差,然后减去并除以这些固定的、预先计算的量。我们在第 2.1.4 节中的图像分类器的预处理中看到了这一点。
我们可以对输入执行几种其他操作,如几何变换(旋转、缩放和裁剪)。这些操作可能有助于训练,或者可能需要使任意输入符合网络的输入要求,比如图像的大小。我们将在第 12.6 节中遇到许多这些策略。现在,只需记住你有可用的图像处理选项即可。
4.2 3D 图像:体积数据
我们已经学会了如何加载和表示 2D 图像,就像我们用相机拍摄的那些图像一样。在某些情境下,比如涉及 CT(计算机断层扫描)扫描的医学成像应用中,我们通常处理沿着头到脚轴堆叠的图像序列,每个图像对应于人体的一个切片。在 CT 扫描中,强度代表了身体不同部位的密度–肺部、脂肪、水、肌肉和骨骼,按照密度递增的顺序–在临床工作站上显示 CT 扫描时,从暗到亮进行映射。每个点的密度是根据穿过身体后到达探测器的 X 射线量计算的,通过一些复杂的数学将原始传感器数据解卷积为完整体积。
CT(计算机断层扫描)只有一个强度通道,类似于灰度图像。这意味着通常情况下,原生数据格式中会省略通道维度;因此,类似于上一节,原始数据通常具有三个维度。通过将单个 2D 切片堆叠成 3D 张量,我们可以构建代表主体的 3D 解剖结构的体积数据。与我们在图 4.1 中看到的情况不同,图 4.2 中的额外维度代表的是物理空间中的偏移,而不是可见光谱中的特定波段。
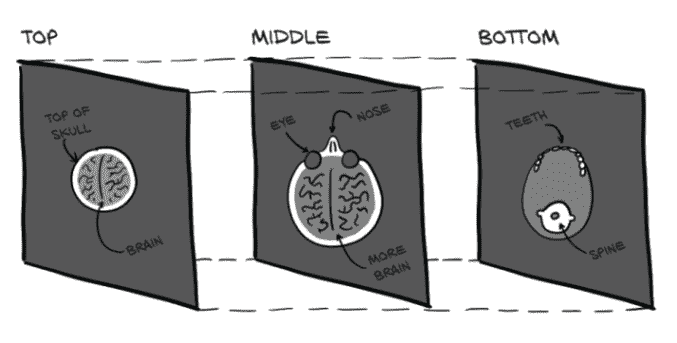
图 4.2 从头部到下颌的 CT 扫描切片
本书的第二部分将致力于解决现实世界中的医学成像问题,因此我们不会深入讨论医学成像数据格式的细节。目前,可以说存储体积数据与图像数据的张量之间没有根本区别。我们只是在通道维度之后多了一个维度,深度,导致了一个形状为N × C × D × H × W的 5D 张量。
4.2.1 加载专用格式
让我们使用imageio模块中的volread函数加载一个样本 CT 扫描,该函数以一个目录作为参数,并将所有数字影像与通信医学(DICOM)文件²组装成一个 NumPy 3D 数组(code/p1ch4/ 2_volumetric_ct.ipynb)。
代码清单 4.2 code/p1ch4/2_volumetric_ct.ipynb
# In[2]:
import imageiodir_path = "../data/p1ch4/volumetric-dicom/2-LUNG 3.0 B70f-04083"
vol_arr = imageio.volread(dir_path, 'DICOM')
vol_arr.shape# Out[2]:
Reading DICOM (examining files): 1/99 files (1.0%99/99 files (100.0%)Found 1 correct series.
Reading DICOM (loading data): 31/99 (31.392/99 (92.999/99 (100.0%)(99, 512, 512)
就像在第 4.1.3 节中所述,布局与 PyTorch 期望的不同,因为没有通道信息。因此,我们将使用unsqueeze为channel维度腾出空间:
# In[3]:
vol = torch.from_numpy(vol_arr).float()
vol = torch.unsqueeze(vol, 0)vol.shape# Out[3]:
torch.Size([1, 99, 512, 512])
此时,我们可以通过沿着batch方向堆叠多个体积来组装一个 5D 数据集,就像我们在上一节中所做的那样。在第二部分中我们将看到更多的 CT 数据。
4.3 表格数据的表示
在机器学习工作中我们会遇到的最简单形式的数据位于电子表格、CSV 文件或数据库中。无论媒介如何,它都是一个包含每个样本(或记录)一行的表格,其中列包含关于我们样本的一条信息。
起初,我们假设表格中样本出现的顺序没有意义:这样的表格是独立样本的集合,不像时间序列那样,其中样本由时间维度相关联。
列可能包含数值,例如特定位置的温度;或标签,例如表示样本属性的字符串,如“蓝色”。因此,表格数据通常不是同质的:不同列的类型不同。我们可能有一列显示苹果的重量,另一列用标签编码它们的颜色。
另一方面,PyTorch 张量是同质的。PyTorch 中的信息通常被编码为一个数字,通常是浮点数(尽管也支持整数类型和布尔类型)。这种数字编码是有意的,因为神经网络是数学实体,通过矩阵乘法和非线性函数的连续应用将实数作为输入并产生实数作为输出。
4.3.1 使用真实世界数据集
作为深度学习从业者的第一项工作是将异构的现实世界数据编码为浮点数张量,以便神经网络消费。互联网上有大量的表格数据集可供免费使用;例如,可以查看github.com/caesar0301/awesome-public-datasets。让我们从一些有趣的东西开始:葡萄酒!葡萄酒质量数据集是一个包含葡萄牙北部绿葡萄酒样本的化学特征和感官质量评分的免费表格。白葡萄酒数据集可以在这里下载:mng.bz/90Ol。为了方便起见,我们还在 Deep Learning with PyTorch Git 存储库中的 data/p1ch4/tabular-wine 目录下创建了数据集的副本。
该文件包含一个逗号分隔的值集合,由一个包含列名的标题行引导。前 11 列包含化学变量的值,最后一列包含从 0(非常糟糕)到 10(优秀)的感官质量评分。这些是数据集中按照它们出现的顺序的列名:
fixed acidity
volatile acidity
citric acid
residual sugar
chlorides
free sulfur dioxide
total sulfur dioxide
density
pH
sulphates
alcohol
quality
在这个数据集上的一个可能的机器学习任务是仅通过化学特征预测质量评分。不过,不用担心;机器学习不会很快消灭品酒。我们必须从某处获取训练数据!正如我们在图 4.3 中看到的,我们希望在我们的数据中的化学列和质量列之间找到一个关系。在这里,我们期望看到随着硫的减少,质量会提高。
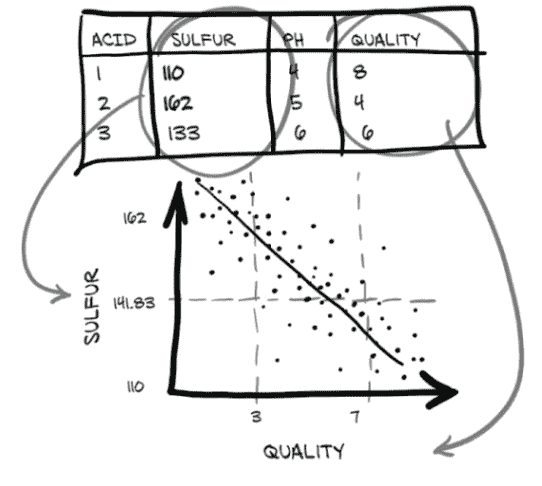
图 4.3 我们(希望)在葡萄酒中硫和质量之间的关系
4.3.2 加载葡萄酒数据张量
然而,在进行这之前,我们需要以一种比在文本编辑器中打开文件更可用的方式来检查数据。让我们看看如何使用 Python 加载数据,然后将其转换为 PyTorch 张量。Python 提供了几种快速加载 CSV 文件的选项。三种流行的选项是
-
Python 自带的
csv模块 -
NumPy
-
Pandas
第三个选项是最节省时间和内存的。然而,我们将避免在我们的学习轨迹中引入额外的库,只是因为我们需要加载一个文件。由于我们在上一节中已经介绍了 NumPy,并且 PyTorch 与 NumPy 有很好的互操作性,我们将选择这个。让我们加载我们的文件,并将生成的 NumPy 数组转换为 PyTorch 张量(code/p1ch4/3_tabular_wine.ipynb)。
代码清单 4.3 code/p1ch4/3_tabular_wine.ipynb
# In[2]:
import csv
wine_path = "../data/p1ch4/tabular-wine/winequality-white.csv"
wineq_numpy = np.loadtxt(wine_path, dtype=np.float32, delimiter=";",skiprows=1)
wineq_numpy# Out[2]:
array([[ 7\. , 0.27, 0.36, ..., 0.45, 8.8 , 6\. ],[ 6.3 , 0.3 , 0.34, ..., 0.49, 9.5 , 6\. ],[ 8.1 , 0.28, 0.4 , ..., 0.44, 10.1 , 6\. ],...,[ 6.5 , 0.24, 0.19, ..., 0.46, 9.4 , 6\. ],[ 5.5 , 0.29, 0.3 , ..., 0.38, 12.8 , 7\. ],[ 6\. , 0.21, 0.38, ..., 0.32, 11.8 , 6\. ]], dtype=float32)
在这里,我们只规定 2D 数组的类型应该是 32 位浮点数,用于分隔每行值的分隔符,以及不应读取第一行,因为它包含列名。让我们检查所有数据是否都已读取
# In[3]:
col_list = next(csv.reader(open(wine_path), delimiter=';'))wineq_numpy.shape, col_list# Out[3]:
((4898, 12),['fixed acidity','volatile acidity','citric acid','residual sugar','chlorides','free sulfur dioxide','total sulfur dioxide','density','pH','sulphates','alcohol','quality'])
然后将 NumPy 数组转换为 PyTorch 张量:
# In[4]:
wineq = torch.from_numpy(wineq_numpy)wineq.shape, wineq.dtype# Out[4]:
(torch.Size([4898, 12]), torch.float32)
此时,我们有一个包含所有列的浮点torch.Tensor,包括最后一列,指的是质量评分。³
连续值、有序值和分类值
当我们试图理解数据时,我们应该意识到三种不同类型的数值。第一种是连续值。当以数字表示时,这些值是最直观的。它们是严格有序的,各个值之间的差异具有严格的含义。声明 A 包比 B 包重 2 千克,或者 B 包比 A 包远 100 英里,无论 A 包是 3 千克还是 10 千克,或者 B 包来自 200 英里还是 2,000 英里,都有固定的含义。如果你在计数或测量带单位的东西,那么它很可能是一个连续值。文献实际上进一步将连续值分为不同类型:在前面的例子中,说某物体重两倍或距离远三倍是有意义的,因此这些值被称为比例尺。另一方面,一天中的时间具有差异的概念,但声称 6:00 比 3:00 晚两倍是不合理的;因此时间只提供一个区间尺度。
接下来是有序值。我们在连续值中具有的严格排序仍然存在,但值之间的固定关系不再适用。一个很好的例子是将小、中、大饮料排序,其中小映射到值 1,中 2,大 3。大饮料比中饮料大,就像 3 比 2 大一样,但这并不告诉我们有多大差异。如果我们将我们的 1、2 和 3 转换为实际容量(比如 8、12 和 24 液体盎司),那么它们将转变为区间值。重要的是要记住,我们不能在值上“做数学运算”以外的排序它们;尝试平均大=3 和小=1 并不会得到中等饮料!
最后,分类值既没有顺序也没有数值含义。这些通常只是分配了任意数字的可能性枚举。将水分配给 1,咖啡分配给 2,苏打分配给 3,牛奶分配给 4 就是一个很好的例子。将水放在第一位,牛奶放在最后一位并没有真正的逻辑;它们只是需要不同的值来区分它们。我们可以将咖啡分配给 10,牛奶分配给-3,这样也不会有显著变化(尽管在范围 0…N - 1 内分配值将对独热编码和我们将在第 4.5.4 节讨论的嵌入有优势)。因为数值值没有含义,它们被称为名义尺度。
4.3.3 表示分数
我们可以将分数视为连续变量,保留为实数,并执行回归任务,或将其视为标签并尝试从化学分析中猜测标签以进行分类任务。在这两种方法中,我们通常会从输入数据张量中删除分数,并将其保留在单独的张量中,以便我们可以将分数用作地面实况,而不将其作为模型的输入:
# In[5]:
data = wineq[:, :-1] # ❶
data, data.shape# Out[5]:
(tensor([[ 7.00, 0.27, ..., 0.45, 8.80],[ 6.30, 0.30, ..., 0.49, 9.50],...,[ 5.50, 0.29, ..., 0.38, 12.80],[ 6.00, 0.21, ..., 0.32, 11.80]]), torch.Size([4898, 11]))# In[6]:
target = wineq[:, -1] # ❷
target, target.shape# Out[6]:
(tensor([6., 6., ..., 7., 6.]), torch.Size([4898]))
❶ 选择所有行和除最后一列之外的所有列
❷ 选择所有行和最后一列
如果我们想要将target张量转换为标签张量,我们有两种选择,取决于策略或我们如何使用分类数据。一种方法是简单地将标签视为整数分数的向量:
# In[7]:
target = wineq[:, -1].long()
target# Out[7]:
tensor([6, 6, ..., 7, 6])
如果目标是字符串标签,比如葡萄酒颜色,为每个字符串分配一个整数编号将让我们遵循相同的方法。
4.3.4 独热编码
另一种方法是构建分数的独热编码:即,将 10 个分数中的每一个编码为一个具有 10 个元素的向量,其中所有元素均设置为 0,但一个元素在每个分数的不同索引上设置为 1。 这样,分数 1 可以映射到向量(1,0,0,0,0,0,0,0,0,0),分数 5 可以映射到(0,0,0,0,1,0,0,0,0,0),依此类推。请注意,分数对应于非零元素的索引纯属偶然:我们可以重新排列分配,从分类的角度来看,没有任何变化。
这两种方法之间有明显的区别。将葡萄酒质量分数保留在整数分数向量中会对分数产生排序–这在这种情况下可能是完全合适的,因为 1 分比 4 分低。它还会在分数之间引入某种距离:也就是说,1 和 3 之间的距离与 2 和 4 之间的距离相同。如果这对我们的数量成立,那就太好了。另一方面,如果分数完全是离散的,比如葡萄品种,独热编码将更适合,因为没有暗示的排序或距离。当分数是连续变量时,独热编码也适用,例如在整数分数之间没有意义的情况下,比如 2.4,对于应用程序来说要么是这个要么是那个。
我们可以使用scatter_方法实现独热编码,该方法将源张量中的值沿提供的索引填充到张量中:
# In[8]:
target_onehot = torch.zeros(target.shape[0], 10)target_onehot.scatter_(1, target.unsqueeze(1), 1.0)# Out[8]:
tensor([[0., 0., ..., 0., 0.],[0., 0., ..., 0., 0.],...,[0., 0., ..., 0., 0.],[0., 0., ..., 0., 0.]])
让我们看看scatter_做了什么。首先,我们注意到它的名称以下划线结尾。正如您在上一章中学到的,这是 PyTorch 中的一种约定,表示该方法不会返回新张量,而是会直接修改张量。scatter_的参数如下:
-
指定以下两个参数的维度
-
指示要散布元素索引的列张量
-
包含要散布的元素或要散布的单个标量的张量(在本例中为 1)
换句话说,前面的调用读取,“对于每一行,取目标标签的索引(在我们的情况下与分数相符)并将其用作列索引设置值为 1.0。” 最终结果是一个编码分类信息的张量。
scatter_的第二个参数,索引张量,需要与我们要散布到的张量具有相同数量的维度。由于target_onehot有两个维度(4,898 × 10),我们需要使用unsqueeze添加一个额外的虚拟维度到target中:
# In[9]:
target_unsqueezed = target.unsqueeze(1)
target_unsqueezed# Out[9]:
tensor([[6],[6],...,[7],[6]])
调用unsqueeze函数会添加一个单例维度,将一个包含 4,898 个元素的 1D 张量转换为一个大小为 (4,898 × 1) 的 2D 张量,而不改变其内容–不会添加额外的元素;我们只是决定使用额外的索引来访问元素。也就是说,我们可以通过target[0]访问target的第一个元素,通过target_unsqueezed[0,0]访问其未挤压的对应元素。
PyTorch 允许我们在训练神经网络时直接使用类索引作为目标。但是,如果我们想将分数用作网络的分类输入,我们将不得不将其转换为一个独热编码张量。
4.3.5 何时进行分类
现在我们已经看到了如何处理连续和分类数据。您可能想知道早期边栏中讨论的有序情况是什么情况。对于这种情况,没有通用的处理方法;最常见的做法是将这些数据视为分类数据(失去排序部分,并希望也许我们的模型在训练过程中会捕捉到它,如果我们只有少数类别)或连续数据(引入一个任意的距离概念)。我们将在图 4.5 中的天气情况中采取后者。我们在图 4.4 中的一个小流程图中总结了我们的数据映射。
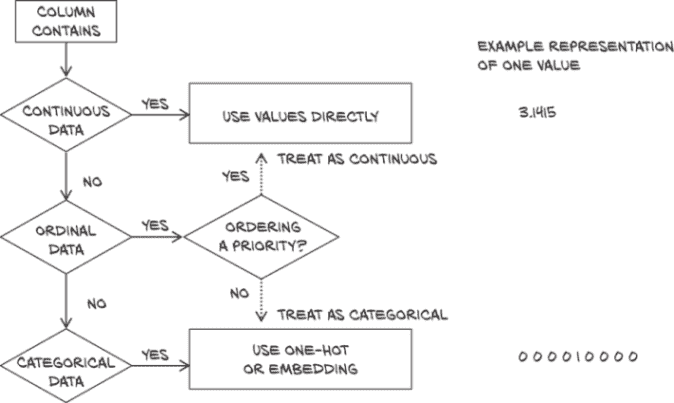
图 4.4 如何处理连续、有序和分类数据的列
让我们回到包含与化学分析相关的 11 个变量的data张量。我们可以使用 PyTorch 张量 API 中的函数以张量形式操作我们的数据。让我们首先获取每列的均值和标准差:
# In[10]:
data_mean = torch.mean(data, dim=0)
data_mean# Out[10]:
tensor([6.85e+00, 2.78e-01, 3.34e-01, 6.39e+00, 4.58e-02, 3.53e+01,1.38e+02, 9.94e-01, 3.19e+00, 4.90e-01, 1.05e+01])# In[11]:
data_var = torch.var(data, dim=0)
data_var# Out[11]:
tensor([7.12e-01, 1.02e-02, 1.46e-02, 2.57e+01, 4.77e-04, 2.89e+02,1.81e+03, 8.95e-06, 2.28e-02, 1.30e-02, 1.51e+00])
在这种情况下,dim=0表示沿着维度 0 执行缩减。此时,我们可以通过减去均值并除以标准差来对数据进行归一化,这有助于学习过程(我们将在第五章的 5.4.4 节中更详细地讨论这一点):
# In[12]:
data_normalized = (data - data_mean) / torch.sqrt(data_var)
data_normalized# Out[12]:
tensor([[ 1.72e-01, -8.18e-02, ..., -3.49e-01, -1.39e+00],[-6.57e-01, 2.16e-01, ..., 1.35e-03, -8.24e-01],...,[-1.61e+00, 1.17e-01, ..., -9.63e-01, 1.86e+00],[-1.01e+00, -6.77e-01, ..., -1.49e+00, 1.04e+00]])
4.3.6 寻找阈值
接下来,让我们开始查看数据,看看是否有一种简单的方法可以一眼看出好酒和坏酒的区别。首先,我们将确定target中对应于得分小于或等于 3 的行:
# In[13]:
bad_indexes = target <= 3 # ❶
bad_indexes.shape, bad_indexes.dtype, bad_indexes.sum()# Out[13]:
(torch.Size([4898]), torch.bool, tensor(20))
❶ PyTorch 还提供比较函数,例如 torch.le(target, 3),但使用运算符似乎是一个很好的标准。
注意,bad_indexes中只有 20 个条目被设置为True!通过使用 PyTorch 中称为高级索引的功能,我们可以使用数据类型为torch.bool的张量来索引data张量。这将基本上将data过滤为仅包含索引张量中为True的项目(或行)的项。bad_indexes张量与target具有相同的形状,其值为False或True,取决于我们的阈值与原始target张量中每个元素之间的比较结果:
# In[14]:
bad_data = data[bad_indexes]
bad_data.shape# Out[14]:
torch.Size([20, 11])
注意,新的bad_data张量有 20 行,与bad_indexes张量中为True的行数相同。它保留了所有 11 列。现在我们可以开始获取关于被分为好、中等和差类别的葡萄酒的信息。让我们对每列进行.mean()操作:
# In[15]:
bad_data = data[target <= 3]
mid_data = data[(target > 3) & (target < 7)] # ❶
good_data = data[target >= 7]bad_mean = torch.mean(bad_data, dim=0)
mid_mean = torch.mean(mid_data, dim=0)
good_mean = torch.mean(good_data, dim=0)for i, args in enumerate(zip(col_list, bad_mean, mid_mean, good_mean)):print('{:2} {:20} {:6.2f} {:6.2f} {:6.2f}'.format(i, *args))# Out[15]:0 fixed acidity 7.60 6.89 6.731 volatile acidity 0.33 0.28 0.272 citric acid 0.34 0.34 0.333 residual sugar 6.39 6.71 5.264 chlorides 0.05 0.05 0.045 free sulfur dioxide 53.33 35.42 34.556 total sulfur dioxide 170.60 141.83 125.257 density 0.99 0.99 0.998 pH 3.19 3.18 3.229 sulphates 0.47 0.49 0.50
10 alcohol 10.34 10.26 11.42
❶ 对于布尔 NumPy 数组和 PyTorch 张量,& 运算符执行逻辑“与”操作。
看起来我们有所发现:乍一看,坏酒似乎具有更高的总二氧化硫含量,等等其他差异。我们可以使用总二氧化硫的阈值作为区分好酒和坏酒的粗略标准。让我们获取总二氧化硫列低于我们之前计算的中点的索引,如下所示:
# In[16]:
total_sulfur_threshold = 141.83
total_sulfur_data = data[:,6]
predicted_indexes = torch.lt(total_sulfur_data, total_sulfur_threshold)predicted_indexes.shape, predicted_indexes.dtype, predicted_indexes.sum()# Out[16]:
(torch.Size([4898]), torch.bool, tensor(2727))
这意味着我们的阈值意味着超过一半的葡萄酒将是高质量的。接下来,我们需要获取实际好葡萄酒的索引:
# In[17]:
actual_indexes = target > 5actual_indexes.shape, actual_indexes.dtype, actual_indexes.sum()# Out[17]:
(torch.Size([4898]), torch.bool, tensor(3258))
由于实际好酒比我们的阈值预测多约 500 瓶,我们已经有了不完美的确凿证据。现在我们需要看看我们的预测与实际排名的匹配程度。我们将在我们的预测索引和实际好酒索引之间执行逻辑“与”(记住每个都只是一个由零和一组成的数组),并使用这些一致的酒来确定我们的表现如何:
# In[18]:
n_matches = torch.sum(actual_indexes & predicted_indexes).item()
n_predicted = torch.sum(predicted_indexes).item()
n_actual = torch.sum(actual_indexes).item()n_matches, n_matches / n_predicted, n_matches / n_actual# Out[18]:
(2018, 0.74000733406674, 0.6193984039287906)
我们大约有 2,000 瓶酒是正确的!由于我们预测了 2,700 瓶酒,这给了我们 74%的机会,如果我们预测一瓶酒是高质量的,那它实际上就是。不幸的是,有 3,200 瓶好酒,我们只识别了其中的 61%。嗯,我们得到了我们签约的东西;这几乎比随机好不了多少!当然,这一切都很天真:我们确切地知道多个变量影响葡萄酒的质量,这些变量的值与结果之间的关系(可能是实际分数,而不是其二值化版本)可能比单个值的简单阈值更复杂。
实际上,一个简单的神经网络将克服所有这些限制,许多其他基本的机器学习方法也将克服这些限制。在接下来的两章中,一旦我们学会如何从头开始构建我们的第一个神经网络,我们将有解决这个问题的工具。我们还将在第十二章重新审视如何更好地评估我们的结果。现在让我们继续探讨其他数据类型。
4.4 处理时间序列
在前一节中,我们讨论了如何表示组织在平面表中的数据。正如我们所指出的,表中的每一行都是独立的;它们的顺序并不重要。或者等效地,没有列编码关于哪些行先出现和哪些行后出现的信息。
回到葡萄酒数据集,我们本可以有一个“年份”列,让我们看看葡萄酒质量是如何逐年演变的。不幸的是,我们手头没有这样的数据,但我们正在努力手动收集数据样本,一瓶一瓶地。在此期间,我们将转向另一个有趣的数据集:来自华盛顿特区自行车共享系统的数据,报告 2011-2012 年 Capital Bikeshare 系统中每小时租赁自行车的数量,以及天气和季节信息(可在此处找到:mng.bz/jgOx)。我们的目标是将一个平面的二维数据集转换为一个三维数据集,如图 4.5 所示。
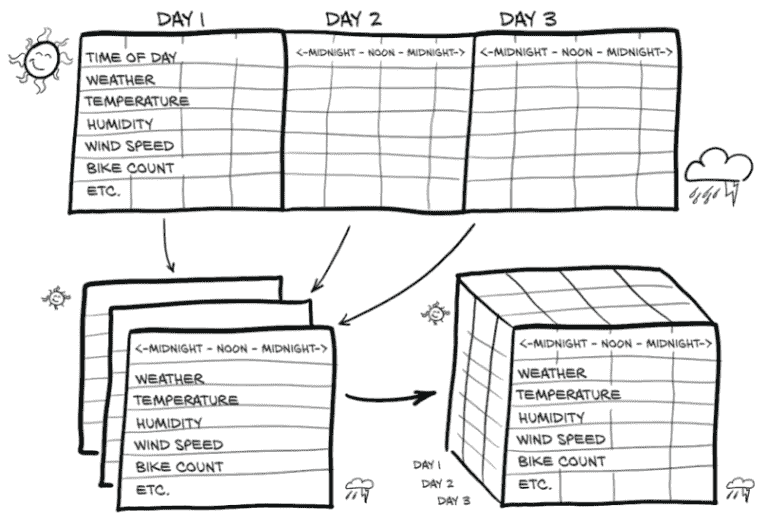
图 4.5 将一维多通道数据集转换为二维多通道数据集,通过将每个样本的日期和小时分开到不同的轴上
4.4.1 添加时间维度
在源数据中,每一行是一个单独的小时数据(图 4.5 显示了这个的转置版本,以更好地适应打印页面)。我们希望改变每小时一行的组织方式,这样我们就有一个轴,它以每个索引增加一天的速度增加,另一个轴代表一天中的小时(与日期无关)。第三个轴将是我们的不同数据列(天气、温度等)。
让我们加载数据(code/p1ch4/4_time_series_bikes.ipynb)。
代码清单 4.4 code/p1ch4/4_time_series_bikes.ipynb
# In[2]:
bikes_numpy = np.loadtxt("../data/p1ch4/bike-sharing-dataset/hour-fixed.csv",dtype=np.float32,delimiter=",",skiprows=1,converters={1: lambda x: float(x[8:10])}) # ❶
bikes = torch.from_numpy(bikes_numpy)
bikes# Out[2]:
tensor([[1.0000e+00, 1.0000e+00, ..., 1.3000e+01, 1.6000e+01],[2.0000e+00, 1.0000e+00, ..., 3.2000e+01, 4.0000e+01],...,[1.7378e+04, 3.1000e+01, ..., 4.8000e+01, 6.1000e+01],[1.7379e+04, 3.1000e+01, ..., 3.7000e+01, 4.9000e+01]])
❶ 将日期字符串转换为对应于第 1 列中的日期的数字
对于每个小时,数据集报告以下变量:
-
记录索引:
instant -
月份的日期:
day -
季节:
season(1:春季,2:夏季,3:秋季,4:冬季) -
年份:
yr(0:2011,1:2012) -
月份:
mnth(1到12) -
小时:
hr(0到23) -
节假日状态:
holiday -
一周的第几天:
weekday -
工作日状态:
workingday -
天气情况:
weathersit(1:晴朗,2:薄雾,3:小雨/小雪,4:大雨/大雪) -
摄氏度温度:
temp -
摄氏度感知温度:
atemp -
湿度:
hum -
风速:
windspeed -
休闲用户数量:
casual -
注册用户数量:
registered -
租赁自行车数量:
cnt
在这样的时间序列数据集中,行代表连续的时间点:有一个维度沿着它们被排序。当然,我们可以将每一行视为独立的,并尝试根据一天中的特定时间来预测循环自行车的数量,而不考虑之前发生了什么。然而,存在排序给了我们利用时间上的因果关系的机会。例如,它允许我们根据较早时间下雨的事实来预测某个时间的骑车次数。目前,我们将专注于学习如何将我们的共享单车数据集转换为我们的神经网络能够以固定大小的块摄入的内容。
这个神经网络模型将需要看到每个不同数量的值的一些序列,比如骑行次数、时间、温度和天气条件:N个大小为C的并行序列。C代表神经网络术语中的通道,对于我们这里的 1D 数据来说,它与列是相同的。N维度代表时间轴,这里每小时一个条目。
4.4.2 按时间段塑造数据
我们可能希望将这两年的数据集分成更宽的观测周期,比如天。这样我们将有N(用于样本数量)个长度为L的C序列集合。换句话说,我们的时间序列数据集将是一个三维张量,形状为N × C × L。C仍然是我们的 17 个通道,而L将是 24:每天的每小时一个。虽然我们必须使用 24 小时的块没有特别的原因,但一般的日常节奏可能会给我们可以用于预测的模式。如果需要,我们也可以使用 7 × 24 = 168 小时块按周划分。所有这些当然取决于我们的数据集具有正确的大小–行数必须是 24 或 168 的倍数。此外,为了使这有意义,我们的时间序列不能有间断。
让我们回到我们的共享单车数据集。第一列是索引(数据的全局排序),第二列是日期,第六列是一天中的时间。我们有一切需要创建每日骑行次数和其他外生变量序列的数据集。我们的数据集已经排序,但如果没有,我们可以使用torch.sort对其进行适当排序。
注意我们使用的文件版本 hour-fixed.csv 已经经过一些处理,包括在原始数据集中包含缺失的行。我们假设缺失的小时没有活跃的自行车(它们通常在清晨的小时内)。
要获得我们的每日小时数据集,我们只需将相同的张量按照 24 小时的批次查看。让我们看一下我们的bikes张量的形状和步幅:
# In[3]:
bikes.shape, bikes.stride()# Out[3]:
(torch.Size([17520, 17]), (17, 1))
这是 17,520 小时,17 列。现在让我们重新塑造数据,使其具有 3 个轴–天、小时,然后我们的 17 列:
# In[4]:
daily_bikes = bikes.view(-1, 24, bikes.shape[1])
daily_bikes.shape, daily_bikes.stride()# Out[4]:
(torch.Size([730, 24, 17]), (408, 17, 1))
这里发生了什么?首先,bikes.shape[1]是 17,即bikes张量中的列数。但这段代码的关键在于对view的调用,这非常重要:它改变了张量查看相同数据的方式,而数据实际上是包含在存储中的。
正如您在上一章中学到的,对张量调用view会返回一个新的张量,它会改变维度和步幅信息,但不会改变存储。这意味着我们可以在基本上零成本地重新排列我们的张量,因为不会复制任何数据。我们调用view需要为返回的张量提供新的形状。我们使用-1作为“剩下的索引数量,考虑到其他维度和原始元素数量”的占位符。
还要记住上一章中提到的存储是一个连续的、线性的数字容器(在本例中是浮点数)。我们的bikes张量将每一行按顺序存储在其相应的存储中。这是通过之前对bikes.stride()的调用输出来确认的。
对于daily_bikes,步幅告诉我们,沿着小时维度(第二维)前进 1 需要我们在存储中前进 17 个位置(或者一组列);而沿着天维度(第一维)前进需要我们前进的元素数量等于存储中一行的长度乘以 24(这里是 408,即 17×24)。
我们看到最右边的维度是原始数据集中的列数。然后,在中间维度,我们有时间,分成 24 个连续小时的块。换句话说,我们现在有一天中L小时的N序列,对应C个通道。为了得到我们期望的N×C×L顺序,我们需要转置张量:
# In[5]:
daily_bikes = daily_bikes.transpose(1, 2)
daily_bikes.shape, daily_bikes.stride()# Out[5]:
(torch.Size([730, 17, 24]), (408, 1, 17))
现在让我们将之前学到的一些技巧应用到这个数据集上。
4.4.3 准备训练
“天气情况”变量是有序的。它有四个级别:1表示好天气,4表示,嗯,非常糟糕。我们可以将这个变量视为分类变量,其中级别被解释为标签,或者作为连续变量。如果我们决定采用分类方式,我们将把变量转换为一个独热编码向量,并将列与数据集连接起来。⁴
为了更容易呈现我们的数据,我们暂时限制在第一天。我们初始化一个以一天中小时数为行数,天气级别数为列数的零填充矩阵:
# In[6]:
first_day = bikes[:24].long()
weather_onehot = torch.zeros(first_day.shape[0], 4)
first_day[:,9]# Out[6]:
tensor([1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 2, 2,2, 2])
然后我们根据每行对应级别向我们的矩阵中散布 1。记住在前几节中使用unsqueeze添加一个单例维度:
# In[7]:
weather_onehot.scatter_(dim=1,index=first_day[:,9].unsqueeze(1).long() - 1, # ❶value=1.0)# Out[7]:
tensor([[1., 0., 0., 0.],[1., 0., 0., 0.],...,[0., 1., 0., 0.],[0., 1., 0., 0.]])
❶ 将值减 1 是因为天气情况范围从 1 到 4,而索引是从 0 开始的
我们的一天从天气“1”开始,以“2”结束,所以这看起来是正确的。
最后,我们使用cat函数将我们的矩阵与原始数据集连接起来。让我们看看我们的第一个结果:
# In[8]:
torch.cat((bikes[:24], weather_onehot), 1)[:1]# Out[8]:
tensor([[ 1.0000, 1.0000, 1.0000, 0.0000, 1.0000, 0.0000, 0.0000,6.0000, 0.0000, 1.0000, 0.2400, 0.2879, 0.8100, 0.0000,3.0000, 13.0000, 16.0000, 1.0000, 0.0000, 0.0000, 0.0000]])
在这里,我们规定我们的原始bikes数据集和我们的独热编码的“天气情况”矩阵沿着列维度(即 1)进行连接。换句话说,两个数据集的列被堆叠在一起;或者等效地,新的独热编码列被附加到原始数据集。为了使cat成功,需要确保张量在其他维度(在这种情况下是行维度)上具有相同的大小。请注意,我们新的最后四列是1, 0, 0, 0,正如我们期望的天气值为 1 时一样。我们也可以对重塑后的daily_bikes张量执行相同操作。记住它的形状是(B, C, L),其中L = 24。我们首先创建一个零张量,具有相同的B和L,但具有C个额外列:
# In[9]:
daily_weather_onehot = torch.zeros(daily_bikes.shape[0], 4,daily_bikes.shape[2])
daily_weather_onehot.shape# Out[9]:
torch.Size([730, 4, 24])
然后我们将独热编码散布到张量的C维度中。由于这个操作是原地执行的,因此只有张量的内容会改变:
# In[10]:
daily_weather_onehot.scatter_(1, daily_bikes[:,9,:].long().unsqueeze(1) - 1, 1.0)
daily_weather_onehot.shape# Out[10]:
torch.Size([730, 4, 24])
并且我们沿着C维度进行连接:
# In[11]:
daily_bikes = torch.cat((daily_bikes, daily_weather_onehot), dim=1)
我们之前提到这不是处理“天气情况”变量的唯一方式。实际上,它的标签具有有序关系,因此我们可以假设它们是连续变量的特殊值。我们可以将变量转换为从 0.0 到 1.0 的范围:
# In[12]:
daily_bikes[:, 9, :] = (daily_bikes[:, 9, :] - 1.0) / 3.0
正如我们在前一节中提到的,将变量重新缩放到[0.0, 1.0]区间或[-1.0, 1.0]区间是我们希望对所有定量变量进行的操作,比如temperature(我们数据集中的第 10 列)。稍后我们会看到为什么要这样做;现在,我们只需说这对训练过程有益。
对变量重新缩放有多种可能性。我们可以将它们的范围映射到[0.0, 1.0]
# In[13]:
temp = daily_bikes[:, 10, :]
temp_min = torch.min(temp)
temp_max = torch.max(temp)
daily_bikes[:, 10, :] = ((daily_bikes[:, 10, :] - temp_min)/ (temp_max - temp_min))
或者减去均值并除以标准差:
# In[14]:
temp = daily_bikes[:, 10, :]
daily_bikes[:, 10, :] = ((daily_bikes[:, 10, :] - torch.mean(temp))/ torch.std(temp))
在后一种情况下,我们的变量将具有 0 均值和单位标准差。如果我们的变量是从高斯分布中抽取的,那么 68%的样本将位于[-1.0, 1.0]区间内。
太棒了:我们建立了另一个不错的数据集,并且看到了如何处理时间序列数据。对于这次的概览,重要的是我们对时间序列的布局有了一个概念,以及我们如何将数据整理成网络可以处理的形式。
其他类型的数据看起来像时间序列,因为有严格的顺序。排在前两位的是什么?文本和音频。接下来我们将看一下文本,而“结论”部分有关于音频的附加示例的链接。
4.5 表示文本
深度学习已经席卷了自然语言处理(NLP)领域,特别是使用重复消耗新输入和先前模型输出组合的模型。这些模型被称为循环神经网络(RNNs),它们已经成功应用于文本分类、文本生成和自动翻译系统。最近,一类名为transformers的网络以更灵活的方式整合过去信息引起了轰动。以前的 NLP 工作负载以包含编码语言语法规则的规则的复杂多阶段管道为特征。现在,最先进的工作是从头开始在大型语料库上端对端训练网络,让这些规则从数据中出现。在过去几年里,互联网上最常用的自动翻译系统基于深度学习。
我们在这一部分的目标是将文本转换为神经网络可以处理的东西:一个数字张量,就像我们之前的情况一样。如果我们能够做到这一点,并且稍后选择适合我们文本处理工作的正确架构,我们就可以使用 PyTorch 进行自然语言处理。我们立即看到这一切是多么强大:我们可以使用相同的 PyTorch 工具在不同领域的许多任务上实现最先进的性能;我们只需要将问题表述得当。这项工作的第一部分是重新塑造数据。
4.5.1 将文本转换为数字
网络在文本上操作有两个特别直观的层次:在字符级别上,逐个处理字符,以及在单词级别上,其中单词是网络所看到的最细粒度的实体。我们将文本信息编码为张量形式的技术,无论我们是在字符级别还是单词级别操作,都是相同的。而且这并不是魔法。我们之前就偶然发现了它:独热编码。
让我们从字符级别的示例开始。首先,让我们获取一些要处理的文本。这里一个了不起的资源是古腾堡计划(www.gutenberg.org)。这是一个志愿者努力,将文化作品数字化并以开放格式免费提供,包括纯文本文件。如果我们的目标是更大规模的语料库,维基百科语料库是一个突出的选择:它是维基百科文章的完整集合,包含 19 亿字和 440 多万篇文章。在英语语料库网站(www.english-corpora.org)可以找到其他语料库。
让我们从古腾堡计划网站加载简·奥斯汀的《傲慢与偏见》:www.gutenberg.org/files/1342/1342-0.txt。我们只需保存文件并读取它(code/p1ch4/5_text_jane_austen.ipynb)。
代码清单 4.5 code/p1ch4/5_text_jane_austen.ipynb
# In[2]:
with open('../data/p1ch4/jane-austen/1342-0.txt', encoding='utf8') as f:text = f.read()
4.5.2 独热编码字符
在我们继续之前,还有一个细节需要注意:编码。这是一个非常广泛的主题,我们只会简单提及。每个书面字符都由一个代码表示:一个适当长度的比特序列,以便每个字符都可以被唯一识别。最简单的编码是 ASCII(美国信息交换标准代码),可以追溯到 1960 年代。ASCII 使用 128 个整数对 128 个字符进行编码。例如,字母a对应于二进制 1100001 或十进制 97,字母b对应于二进制 1100010 或十进制 98,依此类推。这种编码适合 8 位,这在 1965 年是一个很大的优势。
注意 128 个字符显然不足以涵盖所有需要正确表示非英语语言中的书写文本所需的字形、重音、连字等。为此,已经开发了许多使用更多比特作为代码以涵盖更广字符范围的编码。这更广范围的字符被标准化为 Unicode,将所有已知字符映射到数字,这些数字的位表示由特定编码提供。流行的编码包括 UTF-8、UTF-16 和 UTF-32,其中数字分别是 8 位、16 位或 32 位整数序列。Python 3.x 中的字符串是 Unicode 字符串。
我们将对字符进行独热编码。将独热编码限制在对所分析文本有用的字符集上是非常重要的。在我们的情况下,由于我们加载的是英文文本,使用 ASCII 并处理一个小编码是安全的。我们还可以将所有字符转换为小写,以减少编码中不同字符的数量。同样,我们可以筛选掉标点、数字或其他与我们期望的文本类型无关的字符。这可能对神经网络有实际影响,具体取决于手头的任务。
此时,我们需要遍历文本中的字符,并为每个字符提供一个独热编码。每个字符将由一个长度等于编码中不同字符数的向量表示。这个向量将包含除了在编码中字符位置对应的索引处的一个之外的所有零。
我们首先将文本拆分为一系列行,并选择一个任意的行进行关注:
# In[3]:
lines = text.split('\n')
line = lines[200]
line# Out[3]:
'“Impossible, Mr. Bennet, impossible, when I am not acquainted with him'
让我们创建一个能够容纳整行所有独热编码字符总数的张量:
# In[4]:
letter_t = torch.zeros(len(line), 128) # ❶
letter_t.shape# Out[4]:
torch.Size([70, 128])
❶ 由于 ASCII 的限制,128 个硬编码
请注意,letter_t每行保存一个独热编码字符。现在我们只需在正确位置的每行设置一个 1,以便每行表示正确的字符。其中 1 应设置的索引对应于编码中字符的索引:
# In[5]:
for i, letter in enumerate(line.lower().strip()):letter_index = ord(letter) if ord(letter) < 128 else 0 # ❶letter_t[i][letter_index] = 1
❶ 文本使用方向性双引号,这不是有效的 ASCII,因此我们在这里将其筛选掉。
4.5.3 对整个单词进行独热编码
我们已经将我们的句子进行了独热编码,以便神经网络可以理解。单词级别的编码可以通过建立词汇表并对句子–单词序列–进行独热编码来完成。由于词汇表有很多单词,这将产生非常宽的编码向量,这可能不太实用。我们将在下一节看到,在单词级别表示文本有一种更有效的方法,即使用嵌入。现在,让我们继续使用独热编码,看看会发生什么。
我们将定义clean_words,它接受文本并以小写形式返回,并去除标点。当我们在我们的“不可能,本内特先生”line上调用它时,我们得到以下结果:
# In[6]:
def clean_words(input_str):punctuation = '.,;:"!?”“_-'word_list = input_str.lower().replace('\n',' ').split()word_list = [word.strip(punctuation) for word in word_list]return word_listwords_in_line = clean_words(line)
line, words_in_line# Out[6]:
('“Impossible, Mr. Bennet, impossible, when I am not acquainted with him',['impossible','mr','bennet','impossible','when','i','am','not','acquainted','with','him'])
接下来,让我们构建一个单词到编码索引的映射:
# In[7]:
word_list = sorted(set(clean_words(text)))
word2index_dict = {word: i for (i, word) in enumerate(word_list)}len(word2index_dict), word2index_dict['impossible']# Out[7]:
(7261, 3394)
请注意,word2index_dict现在是一个以单词为键、整数为值的字典。我们将使用它来高效地找到一个单词的索引,因为我们对其进行独热编码。现在让我们专注于我们的句子:我们将其分解为单词,并对其进行独热编码–也就是说,我们为每个单词填充一个独热编码向量的张量。我们创建一个空向量,并为句子中的单词分配独热编码值:
# In[8]:
word_t = torch.zeros(len(words_in_line), len(word2index_dict))
for i, word in enumerate(words_in_line):word_index = word2index_dict[word]word_t[i][word_index] = 1print('{:2} {:4} {}'.format(i, word_index, word))print(word_t.shape)# Out[8]:0 3394 impossible1 4305 mr2 813 bennet3 3394 impossible4 7078 when5 3315 i6 415 am7 4436 not8 239 acquainted9 7148 with
10 3215 him
torch.Size([11, 7261])
此时,tensor在大小为 7,261 的编码空间中表示了一个长度为 11 的句子,这是我们字典中的单词数。图 4.6 比较了我们拆分文本的两种选项的要点(以及我们将在下一节中看到的嵌入的使用)。
字符级别和单词级别编码之间的选择让我们需要做出权衡。在许多语言中,字符比单词要少得多:表示字符让我们只表示几个类别,而表示单词则要求我们表示非常多的类别,并且在任何实际应用中,要处理字典中不存在的单词。另一方面,单词传达的意义比单个字符要多得多,因此单词的表示本身就更具信息量。鉴于这两种选择之间的鲜明对比,或许并不奇怪中间方法已经被寻找、发现并成功应用:例如,字节对编码方法⁶从一个包含单个字母的字典开始,然后迭代地将最常见的对添加到字典中,直到达到规定的字典大小。我们的示例句子可能会被分割成这样的标记:⁷
▁Im|pos|s|ible|,|▁Mr|.|▁B|en|net|,|▁impossible|,|▁when|▁I|▁am|▁not|▁acquainted|▁with|▁him
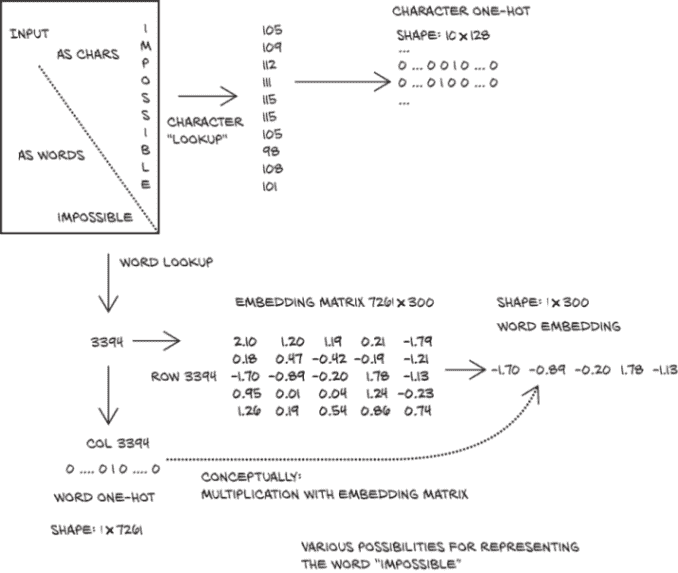
图 4.6 编码单词的三种方式
对于大多数内容,我们的映射只是按单词拆分。但是,较少见的部分–大写的Impossible和名字 Bennet–由子单元组成。
4.5.4 文本嵌入
独热编码是一种在张量中表示分类数据的非常有用的技术。然而,正如我们预料的那样,当要编码的项目数量实际上是无限的时,独热编码开始失效,就像语料库中的单词一样。在仅仅一本书中,我们就有超过 7,000 个项目!
我们当然可以做一些工作来去重单词,压缩替代拼写,将过去和未来时态合并为一个标记,等等。但是,一个通用的英语编码将会非常庞大。更糟糕的是,每当我们遇到一个新单词时,我们都需要向向量中添加一个新列,这意味着需要向模型添加一组新的权重来解释这个新的词汇条目–这将从训练的角度来看是痛苦的。
如何将我们的编码压缩到一个更易管理的大小,并限制大小增长?嗯,与其使用许多零和一个单一的向量,我们可以使用浮点数向量。比如,一个包含 100 个浮点数的向量确实可以表示大量的单词。关键是要找到一种有效的方法,以便将单个单词映射到这个 100 维空间,从而促进下游学习。这被称为嵌入。
原则上,我们可以简单地遍历我们的词汇表,并为每个单词生成一组 100 个随机浮点数。这样做是可以的,因为我们可以将一个非常庞大的词汇表压缩到只有 100 个数字,但它将放弃基于含义或上下文的单词之间距离的概念。使用这种单词嵌入的模型将不得不处理其输入向量中的非常少的结构。一个理想的解决方案是以这样一种方式生成嵌入,使得在相似上下文中使用的单词映射到嵌入的附近区域。
嗯,如果我们要手动设计一个解决这个问题的解决方案,我们可能会决定通过选择将基本名词和形容词映射到轴上来构建我们的嵌入空间。我们可以生成一个 2D 空间,其中轴映射到名词–水果(0.0-0.33)、花朵(0.33-0.66)和狗(0.66-1.0)–和形容词–红色(0.0-0.2)、橙色(0.2-0.4)、黄色(0.4-0.6)、白色(0.6-0.8)和棕色(0.8-1.0)。我们的目标是将实际的水果、花朵和狗放在嵌入中。
当我们开始嵌入词时,我们可以将苹果映射到水果和红色象限中的一个数字。同样,我们可以轻松地将橘子、柠檬、荔枝和猕猴桃(补充我们的五彩水果列表)进行映射。然后我们可以开始处理花朵,并将玫瑰、罂粟花、水仙花、百合花等映射…嗯。不太多棕色的花朵。好吧,向日葵可以被映射到花朵、黄色和棕色,然后雏菊可以被映射到花朵、白色和黄色。也许我们应该将猕猴桃更新为接近水果、棕色和绿色的映射。对于狗和颜色,我们可以将红骨映射到红色附近;嗯,也许狐狸可以代表橙色;金毛寻回犬代表黄色,贵宾犬代表白色,以及…大多数狗都是棕色。
现在我们的嵌入看起来像图 4.7。虽然对于大型语料库来说手动操作并不可行,但请注意,尽管我们的嵌入大小为 2,除了基本的 8 个词之外,我们描述了 15 个不同的词,并且如果我们花时间进行创造性思考,可能还能塞进更多词。

图 4.7 我们的手动词嵌入
正如你可能已经猜到的那样,这种工作可以自动化。通过处理大量的有机文本语料库,类似我们刚刚讨论的嵌入可以生成。主要区别在于嵌入向量中有 100 到 1,000 个元素,并且轴不直接映射到概念:相似概念的词在嵌入空间的相邻区域中映射,其轴是任意的浮点维度。
虽然具体的算法⁹有点超出了我们想要关注的范围,但我们想提一下,嵌入通常是使用神经网络生成的,试图从句子中附近的词(上下文)中预测一个词。在这种情况下,我们可以从单热编码的词开始,并使用一个(通常相当浅的)神经网络生成嵌入。一旦嵌入可用,我们就可以将其用于下游任务。
结果嵌入的一个有趣方面是相似的词不仅聚集在一起,而且与其他词有一致的空间关系。例如,如果我们取苹果的嵌入向量,并开始加减其他词的向量,我们可以开始执行类似苹果-红色-甜+黄色+酸的类比,最终得到一个与柠檬的向量非常相似的向量。
更现代的嵌入模型–BERT 和 GPT-2 甚至在主流媒体中都引起轰动–更加复杂且具有上下文敏感性:也就是说,词汇表中的一个词到向量的映射不是固定的,而是取决于周围的句子。然而,它们通常像我们在这里提到的更简单的经典嵌入一样使用。
4.5.5 文本嵌入作为蓝图
嵌入是一种必不可少的工具,当词汇表中有大量条目需要用数字向量表示时。但在本书中我们不会使用文本和文本嵌入,所以您可能会想知道为什么我们在这里介绍它们。我们认为文本如何表示和处理也可以看作是处理分类数据的一个示例。嵌入在独热编码变得繁琐的地方非常有用。事实上,在先前描述的形式中,它们是一种表示独热编码并立即乘以包含嵌入向量的矩阵的有效方式。
在非文本应用中,我们通常没有能力事先构建嵌入,但我们将从之前避开的随机数开始,并考虑将其改进作为我们学习问题的一部分。这是一种标准技术–以至于嵌入是任何分类数据的独热编码的一个突出替代方案。另一方面,即使我们处理文本,改进预先学习的嵌入在解决手头问题时已经成为一种常见做法。¹⁰
当我们对观察结果的共现感兴趣时,我们之前看到的词嵌入也可以作为一个蓝图。例如,推荐系统–喜欢我们的书的客户也购买了…–使用客户已经互动过的项目作为预测其他可能引起兴趣的上下文。同样,处理文本可能是最常见、最深入研究序列的任务;因此,例如,在处理时间序列任务时,我们可能会从自然语言处理中所做的工作中寻找灵感。
4.6 结论
在本章中,我们涵盖了很多内容。我们学会了加载最常见的数据类型并将其塑造为神经网络可以消费的形式。当然,现实中的数据格式比我们在一本书中描述的要多得多。有些,如医疗史,太复杂了,无法在此处涵盖。其他一些,如音频和视频,被认为对本书的路径不那么关键。然而,如果您感兴趣,我们在书的网站(www.manning.com/books/deep-learning-with-pytorch)和我们的代码库(github.com/deep-learning-with-pytorch/dlwpt-code/ tree/master/p1ch4)提供了音频和视频张量创建的简短示例。
现在我们熟悉了张量以及如何在其中存储数据,我们可以继续迈向本书目标的下一步:教会你训练深度神经网络!下一章将涵盖简单线性模型的学习机制。
4.7 练习
-
使用手机或其他数码相机拍摄几张红色、蓝色和绿色物品的照片(如果没有相机,则可以从互联网上下载一些)。
-
加载每个图像,并将其转换为张量。
-
对于每个图像张量,使用
.mean()方法来了解图像的亮度。 -
获取图像每个通道的平均值。您能仅通过通道平均值识别红色、绿色和蓝色物品吗?
-
-
选择一个包含 Python 源代码的相对较大的文件。
-
构建源文件中所有单词的索引(随意将您的标记化设计得简单或复杂;我们建议从用空格替换
r"[^a-zA-Z0-9_]+"开始)。 -
将您的索引与我们为傲慢与偏见制作的索引进行比较。哪个更大?
-
为源代码文件创建独热编码。
-
使用这种编码会丢失哪些信息?这些信息丢失与傲慢与偏见编码中丢失的信息相比如何?
-
4.8 总结
-
神经网络要求数据表示为多维数值张量,通常是 32 位浮点数。
-
一般来说,PyTorch 期望数据根据模型架构沿特定维度布局–例如,卷积与循环。我们可以使用 PyTorch 张量 API 有效地重塑数据。
-
由于 PyTorch 库与 Python 标准库及周围生态系统的互动方式,加载最常见类型的数据并将其转换为 PyTorch 张量非常方便。
-
图像可以有一个或多个通道。最常见的是典型数字照片的红绿蓝通道。
-
许多图像的每个通道的位深度为 8,尽管每个通道的 12 和 16 位并不罕见。这些位深度都可以存储在 32 位浮点数中而不会丢失精度。
-
单通道数据格式有时会省略显式通道维度。
-
体积数据类似于 2D 图像数据,唯一的区别是添加了第三个维度(深度)。
-
将电子表格转换为张量可能非常简单。分类和有序值列应与间隔值列处理方式不同。
-
文本或分类数据可以通过使用字典编码为一热表示。很多时候,嵌入提供了良好且高效的表示。
这有点轻描淡写:en.wikipedia.org/wiki/Color_model。
来自癌症影像存档的 CPTAC-LSCC 集合:mng.bz/K21K。
作为更深入讨论的起点,请参考 en.wikipedia.org/wiki/Level_of_measurement。
这也可能是一个超越主要路径的情况。可以尝试将一热编码推广到将我们这里的四个类别中的第i个映射到一个向量,该向量在位置 0…i 有一个,其他位置为零。或者–类似于我们在第 4.5.4 节讨论的嵌入–我们可以取嵌入的部分和,这种情况下可能有意义将其设为正值。与我们在实际工作中遇到的许多事物一样,这可能是一个尝试他人有效方法然后以系统化方式进行实验的好地方。
Nadkarni 等人,“自然语言处理:简介”,JAMIA,mng.bz/8pJP。另请参阅 en.wikipedia.org/wiki/Natural-language_processing。
最常由 subword-nmt 和 SentencePiece 库实现。概念上的缺点是字符序列的表示不再是唯一的。
这是从一个在机器翻译数据集上训练的 SentencePiece 分词器。
实际上,通过我们对颜色的一维观点,这是不可能的,因为向日葵的黄色和棕色会平均为白色–但你明白我的意思,而且在更高维度下效果更好。
一个例子是 word2vec: code.google.com/archive/p/word2vec。
这被称为微调。
五、学习的机制
本章涵盖了
-
理解算法如何从数据中学习
-
将学习重新定义为参数估计,使用微分和梯度下降
-
走进一个简单的学习算法
-
PyTorch 如何通过自动求导支持学习
随着过去十年中机器学习的蓬勃发展,从经验中学习的机器的概念已经成为技术和新闻界的主题。那么,机器是如何学习的呢?这个过程的机制是什么–或者说,背后的算法是什么?从观察者的角度来看,一个学习算法被提供了与期望输出配对的输入数据。一旦学习发生,当它被喂入与其训练时的输入数据足够相似的新数据时,该算法将能够产生正确的输出。通过深度学习,即使输入数据和期望输出相距很远,这个过程也能够工作:当它们来自不同的领域时,比如一幅图像和描述它的句子,正如我们在第二章中看到的那样。
5.1 建模中的永恒教训
允许我们解释输入/输出关系的建模模型至少可以追溯到几个世纪前。当德国数学天文学家约翰内斯·开普勒(1571-1630)在 17 世纪初发现他的三大行星运动定律时,他是基于他的导师第谷·布拉赫在裸眼观测(是的,用肉眼看到并写在一张纸上)中收集的数据。没有牛顿的万有引力定律(实际上,牛顿使用了开普勒的工作来解决问题),开普勒推断出了可能适合数据的最简单几何模型。顺便说一句,他花了六年时间盯着他看不懂的数据,连续的领悟,最终制定了这些定律。¹ 我们可以在图 5.1 中看到这个过程。

图 5.1 约翰内斯·开普勒考虑了多个可能符合手头数据的模型,最终选择了一个椭圆。
开普勒的第一定律是:“每颗行星的轨道都是一个椭圆,太阳位于两个焦点之一。”他不知道是什么导致轨道是椭圆的,但是在给定一个行星(或大行星的卫星,比如木星)的一组观测数据后,他可以估计椭圆的形状(离心率)和大小(半通径矢量)。通过从数据中计算出这两个参数,他可以预测行星在天空中的运行轨迹。一旦他弄清楚了第二定律–“连接行星和太阳的一条线在相等的时间间隔内扫过相等的面积”–他也可以根据时间观测推断出行星何时会在空间中的特定位置。²
那么,开普勒如何在没有计算机、口袋计算器甚至微积分的情况下估计椭圆的离心率和大小呢?我们可以从开普勒自己在他的书《新天文学》中的回忆中学到,或者从 J.V.菲尔德在他的一系列文章“证明的起源”中的描述中了解(mng.bz/9007):
本质上,开普勒不得不尝试不同的形状,使用一定数量的观测结果找到曲线,然后使用曲线找到更多位置,用于他有观测结果可用的时间,然后检查这些计算出的位置是否与观测到的位置一致。
–J.V.菲尔德
那么让我们总结一下。在六年的时间里,开普勒
-
从他的朋友布拉赫那里得到了大量的好数据(不是没有一点挣扎)
-
尝试尽可能将其可视化,因为他觉得有些不对劲
-
选择可能适合数据的最简单模型(椭圆)
-
将数据分割,以便他可以处理其中一部分,并保留一个独立的集合用于验证
-
从一个椭圆的初步离心率和大小开始,并迭代直到模型符合观测结果
-
在独立观测上验证了他的模型
-
惊讶地回顾过去
为你准备了一本数据科学手册,一直延续至 1609 年。科学的历史实际上是建立在这七个步骤上的。几个世纪以来,我们已经学会了偏离这些步骤是灾难的前兆。
这正是我们将要从数据中学习的内容。事实上,在这本书中,几乎没有区别是说我们将拟合数据还是让算法从数据中学习。这个过程总是涉及一个具有许多未知参数的函数,其值是从数据中估计的:简而言之,一个模型。
我们可以认为从数据中学习意味着底层模型并非是为解决特定问题而设计的(就像开普勒的椭圆一样),而是能够逼近更广泛函数族的模型。一个神经网络可以非常好地预测第谷·布拉赫的轨迹,而无需开普勒的灵感来尝试将数据拟合成椭圆。然而,艾萨克·牛顿要从一个通用模型中推导出他的引力定律就要困难得多。
在这本书中,我们对不是为解决特定狭窄任务而设计的模型感兴趣,而是可以自动调整以专门为任何一个类似任务进行自我特化的模型–换句话说,根据与手头特定任务相关的数据训练的通用模型。特别是,PyTorch 旨在使创建模型变得容易,使拟合误差对参数的导数能够被解析地表达。如果最后一句话让你完全不明白,别担心;接下来,我们有一个完整的章节希望为你澄清这一点。
本章讨论如何自动化通用函数拟合。毕竟,这就是我们用深度学习做的事情–深度神经网络就是我们谈论的通用函数–而 PyTorch 使这个过程尽可能简单透明。为了确保我们理解关键概念正确,我们将从比深度神经网络简单得多的模型开始。这将使我们能够从本章的第一原则理解学习算法的机制,以便我们可以在第六章转向更复杂的模型。
5.2 学习只是参数估计
在本节中,我们将学习如何利用数据,选择一个模型,并估计模型的参数,以便在新数据上进行良好的预测。为此,我们将把注意力从行星运动的复杂性转移到物理学中第二难的问题:校准仪器。
图 5.2 展示了本章末尾我们将要实现的高层概述。给定输入数据和相应的期望输出(标准答案),以及权重的初始值,模型接收输入数据(前向传播),通过将生成的输出与标准答案进行比较来评估误差的度量。为了优化模型的参数–其权重,使用复合函数的导数链式法则(反向传播)计算单位权重变化后误差的变化(即误差关于参数的梯度)。然后根据导致误差减少的方向更新权重的值。该过程重复进行,直到在未见数据上评估的误差降至可接受水平以下。如果我们刚才说的听起来晦涩难懂,我们有整整一章来澄清事情。到我们完成时,所有的部分都会成为一体,这段文字将变得非常清晰。
现在,我们将处理一个带有嘈杂数据集的问题,构建一个模型,并为其实现一个学习算法。当我们开始时,我们将手工完成所有工作,但在本章结束时,我们将让 PyTorch 为我们完成所有繁重的工作。当我们完成本章时,我们将涵盖训练深度神经网络的许多基本概念,即使我们的激励示例非常简单,我们的模型实际上并不是一个神经网络(但!)。

图 5.2 我们对学习过程的心理模型
5.2.1 一个热门问题
我们刚从某个偏僻的地方旅行回来,带回了一个时髦的壁挂式模拟温度计。它看起来很棒,完全适合我们的客厅。它唯一的缺点是它不显示单位。不用担心,我们有一个计划:我们将建立一个读数和相应温度值的数据集,选择一个模型,迭代调整其权重直到误差的度量足够低,最终能够以我们理解的单位解释新的读数。⁴
让我们尝试按照开普勒使用的相同过程进行。在这个过程中,我们将使用一个他从未拥有过的工具:PyTorch!
5.2.2 收集一些数据
我们将首先记录摄氏度的温度数据和我们新温度计的测量值,并弄清楚事情。几周后,这是数据(code/p1ch5/1_parameter_estimation.ipynb):
# In[2]:
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c)
t_u = torch.tensor(t_u)
这里,t_c值是摄氏度温度,t_u值是我们未知的单位。我们可以预期两个测量中都会有噪音,来自设备本身和我们的近似读数。为了方便起见,我们已经将数据放入张量中;我们将在一分钟内使用它。
5.2.3 可视化数据
图 5.3 中我们数据的快速绘图告诉我们它很嘈杂,但我们认为这里有一个模式。

图 5.3 我们的未知数据可能遵循一个线性模型。
注意 剧透警告:我们知道线性模型是正确的,因为问题和数据都是虚构的,但请耐心等待。这是一个有用的激励性例子,可以帮助我们理解 PyTorch 在幕后做了什么。
5.2.4 选择线性模型作为第一次尝试
在没有进一步的知识的情况下,我们假设将两组测量值之间转换的最简单模型,就像开普勒可能会做的那样。这两者可能是线性相关的–也就是说,通过乘以一个因子并添加一个常数,我们可以得到摄氏度的温度(我们忽略的误差):
t_c = w * t_u + b
这个假设合理吗?可能;我们将看到最终模型的表现如何。我们选择将w和b命名为权重和偏差,这是线性缩放和加法常数的两个非常常见的术语–我们将一直遇到这些术语。⁶
现在,我们需要根据我们拥有的数据来估计w和b,即我们模型中的参数。我们必须这样做,以便通过将未知温度t_u输入模型后得到的温度接近我们实际测量的摄氏度温度。如果这听起来像是在一组测量值中拟合一条直线,那么是的,因为这正是我们正在做的。我们将使用 PyTorch 进行这个简单的例子,并意识到训练神经网络实质上涉及将模型更改为稍微更复杂的模型,其中有一些(或者是一吨)更多的参数。
让我们再次详细说明一下:我们有一个具有一些未知参数的模型,我们需要估计这些参数,以便预测输出和测量值之间的误差尽可能低。我们注意到我们仍然需要准确定义一个误差度量。这样一个度量,我们称之为损失函数,如果误差很大,应该很高,并且应该在完美匹配时尽可能低。因此,我们的优化过程应该旨在找到w和b,使得损失函数最小化。
5.3 较少的损失是我们想要的
损失函数(或成本函数)是一个计算单个数值的函数,学习过程将尝试最小化该数值。损失的计算通常涉及取一些训练样本的期望输出与模型在馈送这些样本时实际产生的输出之间的差异。在我们的情况下,这将是我们的模型输出的预测温度t_p与实际测量值之间的差异:t_p - t_c。
我们需要确保损失函数在t_p大于真实t_c和小于真实t_c时都是正的,因为目标是让t_p匹配t_c。我们有几种选择,最直接的是|t_p - t_c|和(t_p - t_c)²。根据我们选择的数学表达式,我们可以强调或折扣某些错误。概念上,损失函数是一种优先考虑从我们的训练样本中修复哪些错误的方法,以便我们的参数更新导致对高权重样本的输出进行调整,而不是对一些其他样本的输出进行更改,这些样本的损失较小。
这两个示例损失函数在零处有明显的最小值,并且随着预测值向任一方向偏离真值,它们都会单调增加。由于增长的陡峭度也随着远离最小值而单调增加,它们都被称为凸函数。由于我们的模型是线性的,所以损失作为w和b的函数也是凸的。⁷ 损失作为模型参数的凸函数的情况通常很容易处理,因为我们可以通过专门的算法非常有效地找到最小值。然而,在本章中,我们将使用功能更弱但更普遍适用的方法。我们这样做是因为对于我们最终感兴趣的深度神经网络,损失不是输入的凸函数。
对于我们的两个损失函数|t_p - t_c|和(t_p - t_c)²,如图 5.4 所示,我们注意到差的平方在最小值附近的行为更好:对于t_p,误差平方损失的导数在t_p等于t_c时为零。另一方面,绝对值在我们希望收敛的地方具有未定义的导数。实际上,这在实践中并不是问题,但我们暂时将坚持使用差的平方。
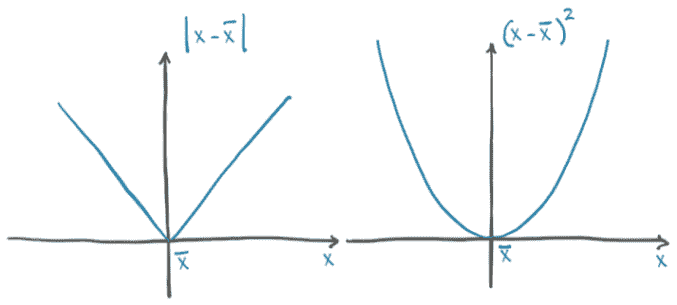
图 5.4 绝对差与差的平方
值得注意的是,平方差也比绝对差惩罚更严重的错误。通常,有更多略微错误的结果比有几个极端错误的结果更好,而平方差有助于按预期优先考虑这些结果。
5.3.1 从问题返回到 PyTorch
我们已经找到了模型和损失函数–我们已经在图 5.2 的高层图片中找到了一个很好的部分。现在我们需要启动学习过程并提供实际数据。另外,数学符号够了;让我们切换到 PyTorch–毕竟,我们来这里是为了乐趣。
我们已经创建了我们的数据张量,现在让我们将模型写成一个 Python 函数:
# In[3]:
def model(t_u, w, b):return w * t_u + b
我们期望t_u,w和b分别是输入张量,权重参数和偏置参数。在我们的模型中,参数将是 PyTorch 标量(也称为零维张量),并且乘法操作将使用广播产生返回的张量。无论如何,是时候定义我们的损失了:
# In[4]:
def loss_fn(t_p, t_c):squared_diffs = (t_p - t_c)**2return squared_diffs.mean()
请注意,我们正在构建一个差异张量,逐元素取平方,最终通过平均所有结果张量中的元素产生一个标量损失函数。这是一个均方损失。
现在我们可以初始化参数,调用模型,
# In[5]:
w = torch.ones(())
b = torch.zeros(())t_p = model(t_u, w, b)
t_p# Out[5]:
tensor([35.7000, 55.9000, 58.2000, 81.9000, 56.3000, 48.9000, 33.9000,21.8000, 48.4000, 60.4000, 68.4000])
并检查损失的值:
# In[6]:
loss = loss_fn(t_p, t_c)
loss# Out[6]:
tensor(1763.8846)
我们在本节中实现了模型和损失。我们终于到达了示例的核心:我们如何估计w和b,使损失达到最小?我们首先手动解决问题,然后学习如何使用 PyTorch 的超能力以更通用、现成的方式解决相同的问题。
广播
我们在第三章提到了广播,并承诺在需要时更仔细地研究它。在我们的例子中,我们有两个标量(零维张量)w和b,我们将它们与长度为 b 的向量(一维张量)相乘并相加。
通常——在 PyTorch 的早期版本中也是如此——我们只能对形状相同的参数使用逐元素二元操作,如加法、减法、乘法和除法。在每个张量中的匹配位置的条目将用于计算结果张量中相应条目。
广播,在 NumPy 中很受欢迎,并被 PyTorch 采用,放宽了大多数二元操作的这一假设。它使用以下规则来匹配张量元素:
-
对于每个索引维度,从后往前计算,如果其中一个操作数在该维度上的大小为 1,则 PyTorch 将使用该维度上的单个条目与另一个张量沿着该维度的每个条目。
-
如果两个大小都大于 1,则它们必须相同,并且使用自然匹配。
-
如果两个张量中一个的索引维度比另一个多,则另一个张量的整体将用于沿着这些维度的每个条目。
这听起来很复杂(如果我们不仔细注意,可能会出错,这就是为什么我们在第 3.4 节中将张量维度命名的原因),但通常,我们可以写下张量维度来看看会发生什么,或者通过使用空间维度来展示广播的方式来想象会发生什么,就像下图所示。
当然,如果没有一些代码示例,这一切都只是理论:
# In[7]:
x = torch.ones(())
y = torch.ones(3,1)
z = torch.ones(1,3)
a = torch.ones(2, 1, 1)
print(f"shapes: x: {x.shape}, y: {y.shape}")
print(f" z: {z.shape}, a: {a.shape}")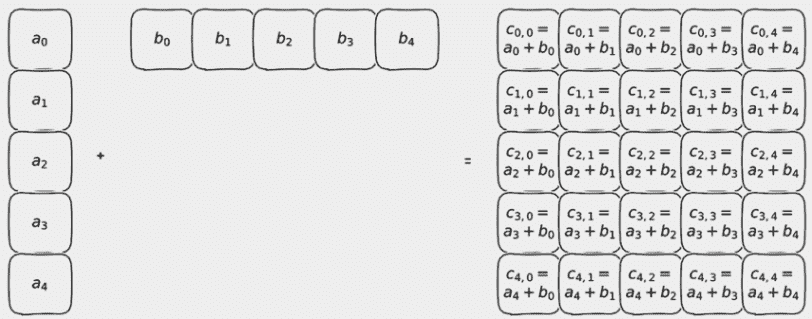
print("x * y:", (x * y).shape)
print("y * z:", (y * z).shape)
print("y * z * a:", (y * z * a).shape)# Out[7]:shapes: x: torch.Size([]), y: torch.Size([3, 1])z: torch.Size([1, 3]), a: torch.Size([2, 1, 1])
x * y: torch.Size([3, 1])y * z: torch.Size([3, 3])5.4 沿着梯度下降
我们将使用梯度下降算法优化参数的损失函数。在本节中,我们将从第一原理建立对梯度下降如何工作的直觉,这将在未来对我们非常有帮助。正如我们提到的,有更有效地解决我们示例问题的方法,但这些方法并不适用于大多数深度学习任务。梯度下降实际上是一个非常简单的想法,并且在具有数百万参数的大型神经网络模型中表现出色。

图 5.5 优化过程的卡通描绘,一个人带有 w 和 b 旋钮,寻找使损失减少的旋钮转动方向
让我们从一个心理形象开始,我们方便地在图 5.5 中勾画出来。假设我们站在一台带有标有w和b的两个旋钮的机器前。我们可以在屏幕上看到损失值,并被告知要将该值最小化。不知道旋钮对损失的影响,我们开始摆弄它们,并为每个旋钮决定哪个方向使损失减少。我们决定将两个旋钮都旋转到损失减少的方向。假设我们离最佳值很远:我们可能会看到损失迅速减少,然后随着接近最小值而减慢。我们注意到在某个时刻,损失再次上升,因此我们反转一个或两个旋钮的旋转方向。我们还了解到当损失变化缓慢时,调整旋钮更精细是个好主意,以避免达到损失再次上升的点。过一段时间,最终,我们收敛到一个最小值。
5.4.1 减小损失
梯度下降与我们刚刚描述的情景并没有太大不同。其思想是计算损失相对于每个参数的变化率,并将每个参数修改为减小损失的方向。就像我们在调节旋钮时一样,我们可以通过向w和b添加一个小数并观察在该邻域内损失的变化来估计变化率:
# In[8]:
delta = 0.1loss_rate_of_change_w = \(loss_fn(model(t_u, w + delta, b), t_c) -loss_fn(model(t_u, w - delta, b), t_c)) / (2.0 * delta)
这意味着在当前w和b的值的邻域内,增加w会导致损失发生一些变化。如果变化是负的,那么我们需要增加w以最小化损失,而如果变化是正的,我们需要减少w。增加多少?根据损失的变化率对w应用变化是个好主意,特别是当损失有几个参数时:我们对那些对损失产生显著变化的参数应用变化。通常,总体上缓慢地改变参数是明智的,因为在当前w值的邻域之外,变化率可能截然不同。因此,我们通常应该通过一个小因子来缩放变化率。这个缩放因子有许多名称;我们在机器学习中使用的是learning_rate:
# In[9]:
learning_rate = 1e-2w = w - learning_rate * loss_rate_of_change_w
我们可以用b做同样的事情:
# In[10]:
loss_rate_of_change_b = \(loss_fn(model(t_u, w, b + delta), t_c) -loss_fn(model(t_u, w, b - delta), t_c)) / (2.0 * delta)b = b - learning_rate * loss_rate_of_change_b
这代表了梯度下降的基本参数更新步骤。通过重复这些评估(并且只要我们选择足够小的学习率),我们将收敛到使给定数据上计算的损失最小的参数的最佳值。我们很快将展示完整的迭代过程,但我们刚刚计算变化率的方式相当粗糙,在继续之前需要进行升级。让我们看看为什么以及如何。
5.4.2 进行分析
通过重复评估模型和损失来计算变化率,以探究在w和b邻域内损失函数的行为的方法在具有许多参数的模型中不具有良好的可扩展性。此外,并不总是清楚邻域应该有多大。我们在前一节中选择了delta等于 0.1,但这完全取决于损失作为w和b函数的形状。如果损失相对于delta变化太快,我们将无法很好地了解损失减少最多的方向。
如果我们可以使邻域无限小,就像图 5.6 中那样,会发生什么?这正是当我们对参数的损失进行导数分析时发生的情况。在我们处理的具有两个或更多参数的模型中,我们计算损失相对于每个参数的各个导数,并将它们放入导数向量中:梯度。

图 5.6 在离散位置评估时下降方向的估计差异与分析方法
计算导数
为了计算损失相对于参数的导数,我们可以应用链式法则,并计算损失相对于其输入(即模型的输出)的导数,乘以模型相对于参数的导数:
d loss_fn / d w = (d loss_fn / d t_p) * (d t_p / d w)
回想一下我们的模型是一个线性函数,我们的损失是平方和。让我们找出导数的表达式。回想一下损失的表达式:
# In[4]:
def loss_fn(t_p, t_c):squared_diffs = (t_p - t_c)**2return squared_diffs.mean()
记住d x² / d x = 2 x,我们得到
# In[11]:
def dloss_fn(t_p, t_c):dsq_diffs = 2 * (t_p - t_c) / t_p.size(0) # ❶return dsq_diffs
❶ 分割是来自均值的导数。
将导数应用于模型
对于模型,回想一下我们的模型是
# In[3]:
def model(t_u, w, b):return w * t_u + b
我们得到这些导数:
# In[12]:
def dmodel_dw(t_u, w, b):return t_u# In[13]:
def dmodel_db(t_u, w, b):return 1.0
定义梯度函数
将所有这些放在一起,返回损失相对于w和b的梯度的函数是
# In[14]:
def grad_fn(t_u, t_c, t_p, w, b):dloss_dtp = dloss_fn(t_p, t_c)dloss_dw = dloss_dtp * dmodel_dw(t_u, w, b)dloss_db = dloss_dtp * dmodel_db(t_u, w, b)return torch.stack([dloss_dw.sum(), dloss_db.sum()]) # ❶
❶ 求和是我们在模型中将参数应用于整个输入向量时隐式执行的广播的反向。
用数学符号表示相同的想法如图 5.7 所示。再次,我们对所有数据点进行平均(即,求和并除以一个常数),以获得每个损失的偏导数的单个标量量。
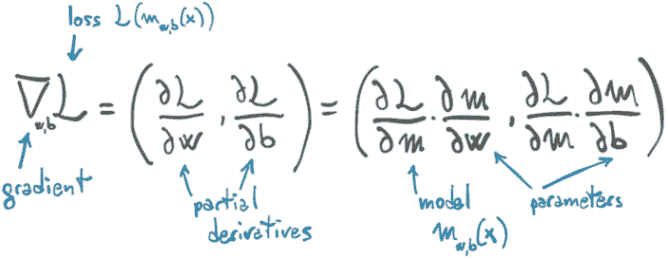
图 5.7 损失函数相对于权重的导数
5.4.3 迭代拟合模型
现在我们已经准备好优化我们的参数了。从参数的一个暂定值开始,我们可以迭代地对其应用更新,进行固定次数的迭代,或直到w和b停止改变。有几个停止标准;现在,我们将坚持固定次数的迭代。
训练循环
既然我们在这里,让我们介绍另一个术语。我们称之为训练迭代,我们在其中为所有训练样本更新参数一个时代。
完整的训练循环如下(code/p1ch5/1_parameter_estimation .ipynb):
# In[15]:
def training_loop(n_epochs, learning_rate, params, t_u, t_c):for epoch in range(1, n_epochs + 1):w, b = paramst_p = model(t_u, w, b) # ❶loss = loss_fn(t_p, t_c)grad = grad_fn(t_u, t_c, t_p, w, b) # ❷params = params - learning_rate * gradprint('Epoch %d, Loss %f' % (epoch, float(loss))) # ❸return params
❶ 正向传播
❷ 反向传播
❸ 这个记录行可能非常冗长。
用于文本输出的实际记录逻辑更复杂(请参见同一笔记本中的第 15 单元:mng.bz/pBB8),但这些差异对于理解本章的核心概念并不重要。
现在,让我们调用我们的训练循环:
# In[17]:
training_loop(n_epochs = 100,learning_rate = 1e-2,params = torch.tensor([1.0, 0.0]),t_u = t_u,t_c = t_c)# Out[17]:
Epoch 1, Loss 1763.884644Params: tensor([-44.1730, -0.8260])Grad: tensor([4517.2969, 82.6000])
Epoch 2, Loss 5802485.500000Params: tensor([2568.4014, 45.1637])Grad: tensor([-261257.4219, -4598.9712])
Epoch 3, Loss 19408035840.000000Params: tensor([-148527.7344, -2616.3933])Grad: tensor([15109614.0000, 266155.7188])
...
Epoch 10, Loss 90901154706620645225508955521810432.000000Params: tensor([3.2144e+17, 5.6621e+15])Grad: tensor([-3.2700e+19, -5.7600e+17])
Epoch 11, Loss infParams: tensor([-1.8590e+19, -3.2746e+17])Grad: tensor([1.8912e+21, 3.3313e+19])tensor([-1.8590e+19, -3.2746e+17])
过度训练
等等,发生了什么?我们的训练过程实际上爆炸了,导致损失变为inf。这清楚地表明params正在接收太大的更新,它们的值开始来回振荡,因为每次更新都超过了,下一个更正得更多。优化过程不稳定:它发散而不是收敛到最小值。我们希望看到对params的更新越来越小,而不是越来越大,如图 5.8 所示。

图 5.8 顶部:由于步长过大,在凸函数(类似抛物线)上发散的优化。底部:通过小步骤收敛的优化。
我们如何限制learning_rate * grad的幅度?嗯,这看起来很容易。我们可以简单地选择一个较小的learning_rate,实际上,当训练不如我们希望的那样顺利时,学习率是我们通常更改的事物之一。我们通常按数量级更改学习率,因此我们可以尝试使用1e-3或1e-4,这将使更新的幅度减少数量级。让我们选择1e-4,看看效果如何:
# In[18]:
training_loop(n_epochs = 100,learning_rate = 1e-4,params = torch.tensor([1.0, 0.0]),t_u = t_u,t_c = t_c)# Out[18]:
Epoch 1, Loss 1763.884644Params: tensor([ 0.5483, -0.0083])Grad: tensor([4517.2969, 82.6000])
Epoch 2, Loss 323.090546Params: tensor([ 0.3623, -0.0118])Grad: tensor([1859.5493, 35.7843])
Epoch 3, Loss 78.929634Params: tensor([ 0.2858, -0.0135])Grad: tensor([765.4667, 16.5122])
...
Epoch 10, Loss 29.105242Params: tensor([ 0.2324, -0.0166])Grad: tensor([1.4803, 3.0544])
Epoch 11, Loss 29.104168Params: tensor([ 0.2323, -0.0169])Grad: tensor([0.5781, 3.0384])
...
Epoch 99, Loss 29.023582Params: tensor([ 0.2327, -0.0435])Grad: tensor([-0.0533, 3.0226])
Epoch 100, Loss 29.022669Params: tensor([ 0.2327, -0.0438])Grad: tensor([-0.0532, 3.0226])tensor([ 0.2327, -0.0438])
不错–行为现在稳定了。但还有另一个问题:参数的更新非常小,因此损失下降非常缓慢,最终停滞。我们可以通过使learning_rate自适应来避免这个问题:即根据更新的幅度进行更改。有一些优化方案可以做到这一点,我们将在本章末尾的第 5.5.2 节中看到其中一个。
然而,在更新项中还有另一个潜在的麻烦制造者:梯度本身。让我们回过头看看在优化期间第 1 个时期的grad。
5.4.4 标准化输入
我们可以看到,权重的第一轮梯度大约比偏置的梯度大 50 倍。这意味着权重和偏置存在于不同比例的空间中。如果是这种情况,一个足够大以便有意义地更新一个参数的学习率对于另一个参数来说会太大而不稳定;而对于另一个参数来说合适的速率将不足以有意义地改变第一个参数。这意味着除非改变问题的表述,否则我们将无法更新我们的参数。我们可以为每个参数设置单独的学习率,但对于具有许多参数的模型来说,这将是太麻烦的事情;这是我们不喜欢的照看的一种方式。
有一个更简单的方法来控制事物:改变输入,使得梯度不那么不同。我们可以确保输入的范围不会远离-1.0到1.0的范围,粗略地说。在我们的情况下,我们可以通过简单地将t_u乘以 0.1 来实现接近这个范围:
# In[19]:
t_un = 0.1 * t_u
在这里,我们通过在变量名后附加一个n来表示t_u的归一化版本。此时,我们可以在我们的归一化输入上运行训练循环:
# In[20]:
training_loop(n_epochs = 100,learning_rate = 1e-2,params = torch.tensor([1.0, 0.0]),t_u = t_un, # ❶t_c = t_c)# Out[20]:
Epoch 1, Loss 80.364342Params: tensor([1.7761, 0.1064])Grad: tensor([-77.6140, -10.6400])
Epoch 2, Loss 37.574917Params: tensor([2.0848, 0.1303])Grad: tensor([-30.8623, -2.3864])
Epoch 3, Loss 30.871077Params: tensor([2.2094, 0.1217])Grad: tensor([-12.4631, 0.8587])
...
Epoch 10, Loss 29.030487Params: tensor([ 2.3232, -0.0710])Grad: tensor([-0.5355, 2.9295])
Epoch 11, Loss 28.941875Params: tensor([ 2.3284, -0.1003])Grad: tensor([-0.5240, 2.9264])
...
Epoch 99, Loss 22.214186Params: tensor([ 2.7508, -2.4910])Grad: tensor([-0.4453, 2.5208])
Epoch 100, Loss 22.148710Params: tensor([ 2.7553, -2.5162])Grad: tensor([-0.4446, 2.5165])tensor([ 2.7553, -2.5162])
❶ 我们已经将t_u更新为我们的新的、重新缩放的t_un。
即使我们将学习率设置回1e-2,参数在迭代更新过程中不会爆炸。让我们看一下梯度:它们的数量级相似,因此对两个参数使用相同的learning_rate效果很好。我们可能可以比简单地乘以 10 进行更好的归一化,但由于这种方法对我们的需求已经足够好,我们暂时将坚持使用这种方法。
注意 这里的归一化绝对有助于训练网络,但你可以提出一个论点,即对于这个特定问题,严格来说并不需要优化参数。这绝对正确!这个问题足够小,有很多方法可以击败参数。然而,对于更大、更复杂的问题,归一化是一个简单而有效(如果不是至关重要!)的工具,用来改善模型的收敛性。
让我们运行足够的迭代次数来看到params的变化变得很小。我们将n_epochs更改为 5,000:
# In[21]:
params = training_loop(n_epochs = 5000,learning_rate = 1e-2,params = torch.tensor([1.0, 0.0]),t_u = t_un,t_c = t_c,print_params = False)params# Out[21]:
Epoch 1, Loss 80.364342
Epoch 2, Loss 37.574917
Epoch 3, Loss 30.871077
...
Epoch 10, Loss 29.030487
Epoch 11, Loss 28.941875
...
Epoch 99, Loss 22.214186
Epoch 100, Loss 22.148710
...
Epoch 4000, Loss 2.927680
Epoch 5000, Loss 2.927648tensor([ 5.3671, -17.3012])
很好:我们的损失在我们沿着梯度下降方向改变参数时减少。它并没有完全降到零;这可能意味着没有足够的迭代次数收敛到零,或者数据点并不完全位于一条直线上。正如我们预料的那样,我们的测量并不完全准确,或者在读数中存在噪音。
但是看:w和b的值看起来非常像我们需要用来将摄氏度转换为华氏度的数字(在我们将输入乘以 0.1 进行归一化之后)。确切的值将是w=5.5556和b=-17.7778。我们时髦的温度计一直显示的是华氏温度。没有什么大的发现,除了我们的梯度下降优化过程有效!
5.4.5 再次可视化
让我们重新审视一下我们一开始做的事情:绘制我们的数据。说真的,这是任何从事数据科学的人都应该做的第一件事。始终大量绘制数据:
# In[22]:
%matplotlib inline
from matplotlib import pyplot as pltt_p = model(t_un, *params) # ❶fig = plt.figure(dpi=600)
plt.xlabel("Temperature (°Fahrenheit)")
plt.ylabel("Temperature (°Celsius)")
plt.plot(t_u.numpy(), t_p.detach().numpy()) # ❷
plt.plot(t_u.numpy(), t_c.numpy(), 'o')
❶ 记住我们是在归一化的未知单位上进行训练。我们还使用参数解包。
❷ 但我们正在绘制原始的未知值。
我们在这里使用了一个名为参数解包的 Python 技巧:*params意味着将params的元素作为单独的参数传递。在 Python 中,这通常是用于列表或元组的,但我们也可以在 PyTorch 张量中使用参数解包,这些张量沿着主导维度分割。因此,在这里,model(t_un, *params)等同于model(t_un, params[0], params[1])。
此代码生成图 5.9。我们的线性模型似乎是数据的一个很好的模型。看起来我们的测量有些不稳定。我们应该给我们的验光师打电话换一副新眼镜,或者考虑退还我们的高级温度计。

图 5.9 我们的线性拟合模型(实线)与输入数据(圆圈)的绘图
5.5 PyTorch 的 autograd:反向传播一切
在我们的小冒险中,我们刚刚看到了反向传播的一个简单示例:我们使用链式法则向后传播导数,计算了函数组合(模型和损失)相对于它们最内部参数(w 和 b)的梯度。这里的基本要求是,我们处理的所有函数都可以在解析上进行微分。如果是这种情况,我们可以一次性计算出相对于参数的梯度–我们之前称之为“损失变化率”。
即使我们有一个包含数百万参数的复杂模型,只要我们的模型是可微的,计算相对于参数的损失梯度就相当于编写导数的解析表达式并评估它们一次。当然,编写一个非常深层次的线性和非线性函数组合的导数的解析表达式并不是一件有趣的事情。这也不是特别快的过程。
5.5.1 自动计算梯度
这就是当 PyTorch 张量发挥作用时的时候,PyTorch 组件 autograd 就派上用场了。第三章介绍了张量是什么以及我们可以在它们上调用什么函数的全面概述。然而,我们遗漏了一个非常有趣的方面:PyTorch 张量可以记住它们的来源,即生成它们的操作和父张量,并且可以自动提供这些操作相对于它们的输入的导数链。这意味着我们不需要手动推导我们的模型;给定一个前向表达式,无论多么嵌套,PyTorch 都会自动提供该表达式相对于其输入参数的梯度。
应用 autograd
此时,继续前进的最佳方式是重新编写我们的温度计校准代码,这次使用 autograd,并看看会发生什么。首先,我们回顾一下我们的模型和损失函数。
code/p1ch5/2_autograd.ipynb
# In[3]:
def model(t_u, w, b):return w * t_u + b# In[4]:
def loss_fn(t_p, t_c):squared_diffs = (t_p - t_c)**2return squared_diffs.mean()
让我们再次初始化一个参数张量:
# In[5]:
params = torch.tensor([1.0, 0.0], requires_grad=True)
使用 grad 属性
注意张量构造函数中的 requires_grad=True 参数?该参数告诉 PyTorch 跟踪由于对 params 进行操作而产生的张量的整个家族树。换句话说,任何将 params 作为祖先的张量都将访问从 params 到该张量的链式函数。如果这些函数是可微的(大多数 PyTorch 张量操作都是可微的),导数的值将自动填充为 params 张量的 grad 属性。
一般来说,所有 PyTorch 张量都有一个名为 grad 的属性。通常,它是 None:
# In[6]:
params.grad is None# Out[6]:
True
我们只需开始一个 requires_grad 设置为 True 的张量,然后调用模型并计算损失,然后在 loss 张量上调用 backward:
# In[7]:
loss = loss_fn(model(t_u, *params), t_c)
loss.backward()params.grad# Out[7]:
tensor([4517.2969, 82.6000])
此时,params 的 grad 属性包含了相对于每个元素的 params 的损失的导数。
当我们在参数 w 和 b 需要梯度时计算我们的 loss 时,除了执行实际计算外,PyTorch 还会创建带有操作(黑色圆圈)的 autograd 图,如图 5.10 顶部行所示。当我们调用 loss.backward() 时,PyTorch 沿着这个图的反向方向遍历以计算梯度,如图的底部行所示的箭头所示。

图 5.10 模型的前向图和后向图,使用 autograd 计算
累积 grad 函数
我们可以有任意数量的张量,其requires_grad设置为True,以及任意组合的函数。在这种情况下,PyTorch 会计算整个函数链(计算图)中损失的导数,并将其值累积在这些张量的grad属性中(图的叶节点)。
警告!大坑在前方。这是 PyTorch 新手——以及许多更有经验的人——经常会遇到的问题。我们刚刚写的是累积,而不是存储。
警告 调用backward会导致导数在叶节点累积。在使用参数更新后,我们需要显式地将梯度清零。
让我们一起重复:调用backward会导致导数在叶节点累积。因此,如果backward在之前被调用,损失会再次被评估,backward会再次被调用(就像在任何训练循环中一样),并且每个叶节点的梯度会累积(即求和)在上一次迭代计算的梯度之上,这会导致梯度的值不正确。
为了防止这种情况发生,我们需要在每次迭代时显式地将梯度清零。我们可以很容易地使用就地zero_方法来实现:
# In[8]:
if params.grad is not None:params.grad.zero_()
注意 你可能会好奇为什么清零梯度是一个必需的步骤,而不是在每次调用backward时自动清零。这样做提供了更多在处理复杂模型中梯度时的灵活性和控制。
将这个提醒铭记在心,让我们看看我们启用自动求导的训练代码是什么样子,从头到尾:
# In[9]:
def training_loop(n_epochs, learning_rate, params, t_u, t_c):for epoch in range(1, n_epochs + 1):if params.grad is not None: # ❶params.grad.zero_()t_p = model(t_u, *params)loss = loss_fn(t_p, t_c)loss.backward()with torch.no_grad(): # ❷params -= learning_rate * params.gradif epoch % 500 == 0:print('Epoch %d, Loss %f' % (epoch, float(loss)))return params
❶ 这可以在调用 loss.backward()之前的循环中的任何时候完成。
❷ 这是一段有些繁琐的代码,但正如我们将在下一节看到的,实际上并不是问题。
请注意,我们更新params的代码并不像我们可能期望的那样直截了当。有两个特殊之处。首先,我们使用 Python 的with语句在no_grad上下文中封装更新。这意味着在with块内,PyTorch 自动求导机制应该不要关注:即,在前向图中不添加边。实际上,当我们执行这段代码时,PyTorch 记录的前向图在我们调用backward时被消耗掉,留下params叶节点。但现在我们想要在开始构建新的前向图之前更改这个叶节点。虽然这种用例通常包含在我们在第 5.5.2 节中讨论的优化器中,但当我们在第 5.5.4 节看到no_grad的另一个常见用法时,我们将更仔细地看一下。
其次,我们就地更新params。这意味着我们保留相同的params张量,但从中减去我们的更新。在使用自动求导时,我们通常避免就地更新,因为 PyTorch 的自动求导引擎可能需要我们将要修改的值用于反向传播。然而,在这里,我们在没有自动求导的情况下操作,保留params张量是有益的。在第 5.5.2 节中向优化器注册参数时,不通过将新张量分配给其变量名来替换参数将变得至关重要。
让我们看看它是否有效:
# In[10]:
training_loop(n_epochs = 5000,learning_rate = 1e-2,params = torch.tensor([1.0, 0.0], requires_grad=True), # ❶t_u = t_un, # ❷t_c = t_c)# Out[10]:
Epoch 500, Loss 7.860116
Epoch 1000, Loss 3.828538
Epoch 1500, Loss 3.092191
Epoch 2000, Loss 2.957697
Epoch 2500, Loss 2.933134
Epoch 3000, Loss 2.928648
Epoch 3500, Loss 2.927830
Epoch 4000, Loss 2.927679
Epoch 4500, Loss 2.927652
Epoch 5000, Loss 2.927647tensor([ 5.3671, -17.3012], requires_grad=True)
❶ 添加 requires_grad=True 至关重要
❷ 再次,我们使用了标准化的 t_un 而不是 t_u。
结果与我们之前得到的相同。对我们来说很好!这意味着虽然我们能够手动计算导数,但我们不再需要这样做。
5.5.2 自选优化器
在示例代码中,我们使用了普通梯度下降进行优化,这对我们简单的情况效果很好。不用说,有几种优化策略和技巧可以帮助收敛,特别是在模型变得复杂时。
我们将在后面的章节深入探讨这个主题,但现在是介绍 PyTorch 如何将优化策略从用户代码中抽象出来的正确时机:也就是我们已经检查过的训练循环。这样可以避免我们不得不手动更新模型的每个参数的样板繁琐工作。torch模块有一个optim子模块,我们可以在其中找到实现不同优化算法的类。这里是一个简略列表(code/p1ch5/3_optimizers.ipynb):
# In[5]:
import torch.optim as optimdir(optim)# Out[5]:
['ASGD','Adadelta','Adagrad','Adam','Adamax','LBFGS','Optimizer','RMSprop','Rprop','SGD','SparseAdam',
...
]
每个优化器构造函数的第一个输入都是参数列表(也称为 PyTorch 张量,通常将requires_grad设置为True)。所有传递给优化器的参数都会被保留在优化器对象内部,因此优化器可以更新它们的值并访问它们的grad属性,如图 5.11 所示。
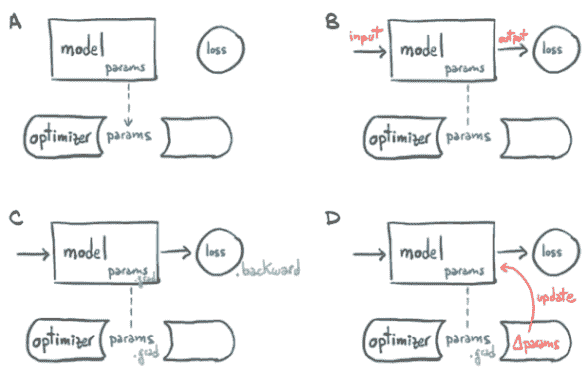
图 5.11(A)优化器如何保存参数的概念表示。(B)从输入计算损失后,(C)调用.backward会使参数上的.grad被填充。(D)此时,优化器可以访问.grad并计算参数更新。
每个优化器都暴露两个方法:zero_grad和step。zero_grad将在构造时将所有传递给优化器的参数的grad属性清零。step根据特定优化器实现的优化策略更新这些参数的值。
使用梯度下降优化器
让我们创建params并实例化一个梯度下降优化器:
# In[6]:
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-5
optimizer = optim.SGD([params], lr=learning_rate)
这里 SGD 代表随机梯度下降。实际上,优化器本身就是一个标准的梯度下降(只要momentum参数设置为0.0,这是默认值)。术语随机来自于梯度通常是通过对所有输入样本的随机子集进行平均得到的,称为小批量。然而,优化器不知道损失是在所有样本(标准)上评估的还是在它们的随机子集(随机)上评估的,所以在这两种情况下算法实际上是相同的。
无论如何,让我们尝试一下我们新的优化器:
# In[7]:
t_p = model(t_u, *params)
loss = loss_fn(t_p, t_c)
loss.backward()optimizer.step()params# Out[7]:
tensor([ 9.5483e-01, -8.2600e-04], requires_grad=True)
在调用step时,params的值会被更新,而无需我们自己操作!发生的情况是,优化器查看params.grad并更新params,从中减去learning_rate乘以grad,与我们以前手动编写的代码完全相同。
准备将这段代码放入训练循环中?不!几乎让我们犯了大错–我们忘记了将梯度清零。如果我们在循环中调用之前的代码,梯度会在每次调用backward时在叶子节点中累积,我们的梯度下降会一团糟!这是循环准备就绪的代码,正确位置是在backward调用之前额外加上zero_grad:
# In[8]:
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-2
optimizer = optim.SGD([params], lr=learning_rate)t_p = model(t_un, *params)
loss = loss_fn(t_p, t_c)optimizer.zero_grad() # ❶
loss.backward()
optimizer.step()params# Out[8]:
tensor([1.7761, 0.1064], requires_grad=True)
❶ 与以前一样,这个调用的确切位置有些随意。它也可以在循环中较早的位置。
太棒了!看看optim模块如何帮助我们将特定的优化方案抽象出来?我们所要做的就是向其提供一个参数列表(该列表可能非常长,对于非常深的神经网络模型是必需的),然后我们可以忘记细节。
让我们相应地更新我们的训练循环:
# In[9]:
def training_loop(n_epochs, optimizer, params, t_u, t_c):for epoch in range(1, n_epochs + 1):t_p = model(t_u, *params)loss = loss_fn(t_p, t_c)optimizer.zero_grad()loss.backward()optimizer.step()if epoch % 500 == 0:print('Epoch %d, Loss %f' % (epoch, float(loss)))return params# In[10]:
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-2
optimizer = optim.SGD([params], lr=learning_rate) # ❶training_loop(n_epochs = 5000,optimizer = optimizer,params = params, # ❶t_u = t_un,t_c = t_c)# Out[10]:
Epoch 500, Loss 7.860118
Epoch 1000, Loss 3.828538
Epoch 1500, Loss 3.092191
Epoch 2000, Loss 2.957697
Epoch 2500, Loss 2.933134
Epoch 3000, Loss 2.928648
Epoch 3500, Loss 2.927830
Epoch 4000, Loss 2.927680
Epoch 4500, Loss 2.927651
Epoch 5000, Loss 2.927648tensor([ 5.3671, -17.3012], requires_grad=True)
❶ 很重要的一点是两个参数必须是同一个对象;否则优化器将不知道模型使用了哪些参数。
再次得到与以前相同的结果。太好了:这进一步证实了我们知道如何手动下降梯度!
测试其他优化器
为了测试更多的优化器,我们只需实例化一个不同的优化器,比如Adam,而不是SGD。其余代码保持不变。非常方便。
我们不会详细讨论 Adam;可以说,它是一种更复杂的优化器,其中学习率是自适应设置的。此外,它对参数的缩放不太敏感–如此不敏感,以至于我们可以回到使用原始(非归一化)输入t_u,甚至将学习率增加到1e-1,Adam 也不会有任何反应:
# In[11]:
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-1
optimizer = optim.Adam([params], lr=learning_rate) # ❶training_loop(n_epochs = 2000,optimizer = optimizer,params = params,t_u = t_u, # ❷t_c = t_c)# Out[11]:
Epoch 500, Loss 7.612903
Epoch 1000, Loss 3.086700
Epoch 1500, Loss 2.928578
Epoch 2000, Loss 2.927646tensor([ 0.5367, -17.3021], requires_grad=True)
❶ 新的优化器类
❷ 我们又回到了将t_u作为我们的输入。
优化器并不是我们训练循环中唯一灵活的部分。让我们将注意力转向模型。为了在相同数据和相同损失上训练神经网络,我们需要改变的只是model函数。在这种情况下并没有特别意义,因为我们知道将摄氏度转换为华氏度相当于进行线性变换,但我们还是会在第六章中这样做。我们很快就会看到,神经网络允许我们消除对我们应该逼近的函数形状的任意假设。即使如此,我们将看到神经网络如何在基础过程高度非线性时进行训练(例如在描述图像与句子之间的情况,正如我们在第二章中看到的)。
我们已经涉及了许多基本概念,这些概念将使我们能够在了解内部运作的情况下训练复杂的深度学习模型:反向传播来估计梯度,自动微分,以及使用梯度下降或其他优化器来优化模型的权重。实际上,并没有太多内容。其余的大部分内容都是填空,无论填空有多广泛。
接下来,我们将提供一个关于如何分割样本的插曲,因为这为学习如何更好地控制自动微分提供了一个完美的用例。
5.5.3 训练、验证和过拟合
约翰内斯·开普勒教给我们一个迄今为止我们没有讨论过的最后一件事,记得吗?他将部分数据保留在一边,以便可以在独立观测上验证他的模型。这是一件至关重要的事情,特别是当我们采用的模型可能近似于任何形状的函数时,就像神经网络的情况一样。换句话说,一个高度适应的模型将倾向于使用其许多参数来确保损失在数据点处最小化,但我们无法保证模型在数据点之外或之间的表现。毕竟,这就是我们要求优化器做的事情:在数据点处最小化损失。毫无疑问,如果我们有一些独立的数据点,我们没有用来评估损失或沿着其负梯度下降,我们很快就会发现,在这些独立数据点上评估损失会产生比预期更高的损失。我们已经提到了这种现象,称为过拟合。
我们可以采取的第一步对抗过拟合的行动是意识到它可能发生。为了做到这一点,正如开普勒在 1600 年发现的那样,我们必须从数据集中取出一些数据点(验证集),并仅在剩余数据点上拟合我们的模型(训练集),如图 5.12 所示。然后,在拟合模型时,我们可以在训练集上评估损失一次,在验证集上评估损失一次。当我们试图决定我们是否已经很好地将模型拟合到数据时,我们必须同时看两者!

图 5.12 数据生成过程的概念表示以及训练数据和独立验证数据的收集和使用。
评估训练损失
训练损失将告诉我们,我们的模型是否能够完全拟合训练集——换句话说,我们的模型是否具有足够的容量来处理数据中的相关信息。如果我们神秘的温度计以对数刻度测量温度,我们可怜的线性模型将无法拟合这些测量值,并为我们提供一个合理的摄氏度转换。在这种情况下,我们的训练损失(在训练循环中打印的损失)会在接近零之前停止下降。
深度神经网络可以潜在地逼近复杂的函数,只要神经元的数量,因此参数的数量足够多。参数数量越少,我们的网络将能够逼近的函数形状就越简单。所以,规则 1:如果训练损失不降低,那么模型对数据来说可能太简单了。另一种可能性是我们的数据只包含让其解释输出的有意义信息:如果商店里的好人卖给我们一个气压计而不是温度计,我们将很难仅凭压力来预测摄氏度,即使我们使用魁北克最新的神经网络架构(www.umontreal.ca/en/artificialintelligence)。
泛化到验证集
那验证集呢?如果在验证集中评估的损失不随着训练集一起减少,这意味着我们的模型正在改善对训练期间看到的样本的拟合,但没有泛化到这个精确集之外的样本。一旦我们在新的、以前未见过的点上评估模型,损失函数的值就会很差。所以,规则 2:如果训练损失和验证损失发散,我们就过拟合了。
让我们深入探讨这种现象,回到我们的温度计示例。我们可以决定用更复杂的函数来拟合数据,比如分段多项式或非常大的神经网络。它可能会生成一个模型,沿着数据点蜿蜒前进,就像图 5.13 中所示,只是因为它将损失推得非常接近零。由于函数远离数据点的行为不会增加损失,因此没有任何东西可以限制模型对训练数据点之外的输入。

图 5.13 过拟合的极端示例
那么,治疗方法呢?好问题。从我们刚才说的来看,过拟合看起来确实是确保模型在数据点之间的行为对我们试图逼近的过程是合理的问题。首先,我们应该确保我们为该过程收集足够的数据。如果我们通过以低频率定期对正弦过程进行采样来收集数据,我们将很难将模型拟合到它。
假设我们有足够的数据点,我们应该确保能够拟合训练数据的模型在它们之间尽可能地规则。有几种方法可以实现这一点。一种方法是向损失函数添加惩罚项,使模型更平滑、变化更慢(在一定程度上)更便宜。另一种方法是向输入样本添加噪声,人为地在训练数据样本之间创建新的数据点,并迫使模型尝试拟合这些数据点。还有其他几种方法,所有这些方法都与这些方法有些相关。但我们可以为自己做的最好的事情,至少作为第一步,是使我们的模型更简单。从直觉上讲,一个简单的模型可能不会像一个更复杂的模型那样完美地拟合训练数据,但它可能在数据点之间的行为更加规则。
我们在这里有一些不错的权衡。一方面,我们需要模型具有足够的容量来适应训练集。另一方面,我们需要模型避免过拟合。因此,为了选择神经网络模型的正确参数大小,该过程基于两个步骤:增加大小直到适应,然后缩小直到停止过拟合。
我们将在第十二章中更多地了解这一点–我们将发现我们的生活将是在拟合和过拟合之间的平衡。现在,让我们回到我们的例子,看看我们如何将数据分成训练集和验证集。我们将通过相同的方式对t_u和t_c进行洗牌,然后将结果洗牌后的张量分成两部分。
分割数据集
对张量的元素进行洗牌相当于找到其索引的排列。randperm函数正是这样做的:
# In[12]:
n_samples = t_u.shape[0]
n_val = int(0.2 * n_samples)shuffled_indices = torch.randperm(n_samples)train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]train_indices, val_indices # ❶# Out[12]:
(tensor([9, 6, 5, 8, 4, 7, 0, 1, 3]), tensor([ 2, 10]))
❶ 由于这些是随机的,如果你的数值与这里的不同,不要感到惊讶。
我们刚刚得到了索引张量,我们可以使用它们从数据张量开始构建训练和验证集:
# In[13]:
train_t_u = t_u[train_indices]
train_t_c = t_c[train_indices]val_t_u = t_u[val_indices]
val_t_c = t_c[val_indices]train_t_un = 0.1 * train_t_u
val_t_un = 0.1 * val_t_u
我们的训练循环并没有真正改变。我们只是想在每个时代额外评估验证损失,以便有机会识别我们是否过拟合:
# In[14]:
def training_loop(n_epochs, optimizer, params, train_t_u, val_t_u,train_t_c, val_t_c):for epoch in range(1, n_epochs + 1):train_t_p = model(train_t_u, *params) # ❶train_loss = loss_fn(train_t_p, train_t_c)val_t_p = model(val_t_u, *params) # ❶val_loss = loss_fn(val_t_p, val_t_c)optimizer.zero_grad()train_loss.backward() # ❷optimizer.step()if epoch <= 3 or epoch % 500 == 0:print(f"Epoch {epoch}, Training loss {train_loss.item():.4f},"f" Validation loss {val_loss.item():.4f}")return params# In[15]:
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-2
optimizer = optim.SGD([params], lr=learning_rate)training_loop(n_epochs = 3000,optimizer = optimizer,params = params,train_t_u = train_t_un, # ❸val_t_u = val_t_un, # ❸train_t_c = train_t_c,val_t_c = val_t_c)# Out[15]:
Epoch 1, Training loss 66.5811, Validation loss 142.3890
Epoch 2, Training loss 38.8626, Validation loss 64.0434
Epoch 3, Training loss 33.3475, Validation loss 39.4590
Epoch 500, Training loss 7.1454, Validation loss 9.1252
Epoch 1000, Training loss 3.5940, Validation loss 5.3110
Epoch 1500, Training loss 3.0942, Validation loss 4.1611
Epoch 2000, Training loss 3.0238, Validation loss 3.7693
Epoch 2500, Training loss 3.0139, Validation loss 3.6279
Epoch 3000, Training loss 3.0125, Validation loss 3.5756tensor([ 5.1964, -16.7512], requires_grad=True)
❶ 这两对行是相同的,除了 train_* vs. val_*输入。
❷ 注意这里没有val_loss.backward(),因为我们不想在验证数据上训练模型。
❸ 由于我们再次使用 SGD,我们又回到了使用归一化的输入。
在这里,我们对我们的模型并不完全公平。验证集真的很小,因此验证损失只有到一定程度才有意义。无论如何,我们注意到验证损失高于我们的训练损失,尽管不是数量级。我们期望模型在训练集上表现更好,因为模型参数是由训练集塑造的。我们的主要目标是看到训练损失和验证损失都在减小。虽然理想情况下,两个损失值应该大致相同,但只要验证损失保持与训练损失相当接近,我们就知道我们的模型继续学习关于我们数据的泛化内容。在图 5.14 中,情况 C 是理想的,而 D 是可以接受的。在情况 A 中,模型根本没有学习;在情况 B 中,我们看到过拟合。我们将在第十二章看到更有意义的过拟合示例。

图 5.14 当查看训练(实线)和验证(虚线)损失时的过拟合情况。 (A) 训练和验证损失不减少;模型由于数据中没有信息或模型容量不足而无法学习。 (B) 训练损失减少,而验证损失增加:过拟合。 © 训练和验证损失完全同步减少。性能可能进一步提高,因为模型尚未达到过拟合的极限。 (D) 训练和验证损失具有不同的绝对值,但趋势相似:过拟合得到控制。
5.5.4 自动微分细节和关闭它
从之前的训练循环中,我们可以看到我们只在train_loss上调用backward。因此,错误只会基于训练集反向传播–验证集用于提供对模型在未用于训练的数据上输出准确性的独立评估。
在这一点上,好奇的读者可能会有一个问题的雏形。模型被评估两次–一次在train_t_u上,一次在val_t_u上–然后调用backward。这不会让自动微分混乱吗?backward会受到在验证集上传递期间生成的值的影响吗?
幸运的是,这种情况并不会发生。训练循环中的第一行评估model在train_t_u上产生train_t_p。然后从train_t_p评估train_loss。这创建了一个计算图,将train_t_u链接到train_t_p到train_loss。当再次在val_t_u上评估model时,它会产生val_t_p和val_loss。在这种情况下,将创建一个将val_t_u链接到val_t_p到val_loss的单独计算图。相同的张量已经通过相同的函数model和loss_fn运行,生成了不同的计算图,如图 5.15 所示。
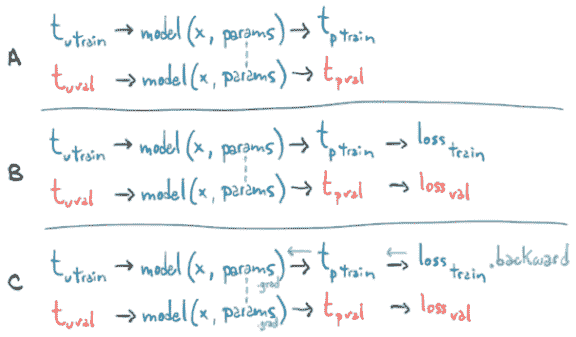
图 5.15 显示当在其中一个上调用.backward 时,梯度如何通过具有两个损失的图传播
这两个图唯一共同拥有的张量是参数。当我们在train_loss上调用backward时,我们在第一个图上运行backward。换句话说,我们根据从train_t_u生成的计算累积train_loss相对于参数的导数。
如果我们(错误地)在val_loss上也调用了backward,那么我们将在相同的叶节点上累积val_loss相对于参数的导数。还记得zero_grad的事情吗?每次我们调用backward时,梯度都会累积在一起,除非我们明确地将梯度清零?嗯,在这里会发生类似的事情:在val_loss上调用backward会导致梯度在params张量中累积,这些梯度是在train_loss.backward()调用期间生成的。在这种情况下,我们实际上会在整个数据集上训练我们的模型(包括训练和验证),因为梯度会依赖于两者。非常有趣。
这里还有另一个讨论的要素。由于我们从未在val_loss上调用backward,那么我们为什么要首先构建计算图呢?实际上,我们可以只调用model和loss_fn作为普通函数,而不跟踪计算。然而,构建自动求导图虽然经过了优化,但会带来额外的成本,在验证过程中我们完全可以放弃这些成本,特别是当模型有数百万个参数时。
为了解决这个问题,PyTorch 允许我们在不需要时关闭自动求导,使用torch.no_grad上下文管理器。在我们的小问题上,我们不会看到任何关于速度或内存消耗方面的有意义的优势。然而,对于更大的模型,差异可能会累积。我们可以通过检查val_loss张量的requires_grad属性的值来确保这一点:
# In[16]:
def training_loop(n_epochs, optimizer, params, train_t_u, val_t_u,train_t_c, val_t_c):for epoch in range(1, n_epochs + 1):train_t_p = model(train_t_u, *params)train_loss = loss_fn(train_t_p, train_t_c)with torch.no_grad(): # ❶val_t_p = model(val_t_u, *params)val_loss = loss_fn(val_t_p, val_t_c)assert val_loss.requires_grad == False # ❷optimizer.zero_grad()train_loss.backward()optimizer.step()
❶ 这里是上下文管理器
❷ 检查我们的输出requires_grad参数在此块内被强制为 False
使用相关的set_grad_enabled上下文,我们还可以根据布尔表达式(通常表示我们是在训练还是推理模式下运行)来条件运行代码,启用或禁用autograd。例如,我们可以定义一个calc_forward函数,根据布尔train_is参数,以有或无自动求导的方式运行model和loss_fn:
# In[17]:
def calc_forward(t_u, t_c, is_train):with torch.set_grad_enabled(is_train):t_p = model(t_u, *params)loss = loss_fn(t_p, t_c)return loss
5.6 结论
我们从一个大问题开始了这一章:机器如何能够从示例中学习?我们在本章的其余部分描述了优化模型以拟合数据的机制。我们选择坚持使用简单模型,以便在不需要的复杂性的情况下看到所有移动部件。
现在我们已经品尝了开胃菜,在第六章中我们终于要进入主菜了:使用神经网络来拟合我们的数据。我们将继续解决相同的温度计问题,但使用torch.nn模块提供的更强大工具。我们将采用相同的精神,使用这个小问题来说明 PyTorch 的更大用途。这个问题不需要神经网络来找到解决方案,但它将让我们更简单地了解训练神经网络所需的内容。
5.7 练习
-
重新定义模型为
w2 * t_u ** 2 + w1 * t_u + b。-
哪些部分的训练循环等需要更改以适应这个重新定义?
-
哪些部分对于更换模型是不可知的?
-
训练后损失是更高还是更低?
-
实际结果是更好还是更差?
-
5.8 总结
-
线性模型是用来拟合数据的最简单合理的模型。
-
凸优化技术可以用于线性模型,但不适用于神经网络,因此我们专注于随机梯度下降进行参数估计。
-
深度学习可以用于通用模型,这些模型并非专门用于解决特定任务,而是可以自动适应并专门化解决手头的问题。
-
学习算法涉及根据观察结果优化模型参数。损失函数是执行任务时的错误度量,例如预测输出与测量值之间的误差。目标是尽可能降低损失函数。
-
损失函数相对于模型参数的变化率可用于更新相同参数以减少损失。
-
PyTorch 中的
optim模块提供了一系列用于更新参数和最小化损失函数的现成优化器。 -
优化器使用 PyTorch 的 autograd 功能来计算每个参数的梯度,具体取决于该参数对最终输出的贡献。这使用户在复杂的前向传递过程中依赖于动态计算图。
-
像
with torch.no_grad():这样的上下文管理器可用于控制 autograd 的行为。 -
数据通常被分成独立的训练样本集和验证样本集。这使我们能够在未经训练的数据上评估模型。
-
过拟合模型发生在模型在训练集上的表现继续改善但在验证集上下降的情况下。这通常是由于模型没有泛化,而是记忆了训练集的期望输出。
¹ 据物理学家迈克尔·福勒回忆:mng.bz/K2Ej。
² 理解开普勒定律的细节并不是理解本章所需的,但你可以在en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion找到更多信息。
³ 除非你是理论物理学家 😉.
⁴ 这个任务——将模型输出拟合为第四章讨论的类型的连续值——被称为回归问题。在第七章和第 2 部分中,我们将关注分类问题。
⁵ 本章的作者是意大利人,所以请原谅他使用合理的单位。
⁶ 权重告诉我们给定输入对输出的影响程度。偏差是如果所有输入都为零时的输出。
⁷ 与图 5.6 中显示的函数形成对比,该函数不是凸的。
⁸ 这个的花哨名称是超参数调整。超参数指的是我们正在训练模型的参数,但超参数控制着这个训练的进行方式。通常这些是手动设置的。特别是,它们不能成为同一优化的一部分。
⁹ 或许是吧;我们不会判断你周末怎么过!
¹⁰ 糟糕!现在周六我们要做什么?
¹¹ 实际上,它将跟踪使用原地操作更改参数的情况。
¹² 我们不应认为使用 torch.no_grad 必然意味着输出不需要梯度。在特定情况下(涉及视图,如第 3.8.1 节所讨论的),即使在 no_grad 上下文中创建时,requires_grad 也不会设置为 False。如果需要确保,最好使用 detach 函数。