在前两章，我们学的是：线性回归，逻辑回归，深度学习(神经网络)，决策树，随即森林算法。他们都是监督学习的例子。

在这一章里，我们将学习非监督学习的算法。

什么是聚类算法：

聚类算法是一种无监督学习方法，用于将数据集中的样本分为不同的组或簇，使得同一组内的样本彼此相似，而不同组之间的样本则具有较大的差异性。聚类算法的目标是发现数据中的内在结构，将相似的样本聚集在一起。

 

就像上图这样把我们的得到的数据进行分类，分类到同一个集合中。

K均值聚类（K-means Clustering）： 

过程主要分为两步：

第一步：随机确定聚类的中心点，第二步，任取图中的已有的点，根据远近，确定它们属于哪一个聚类，第三步，重新根据这些分类过后的点，重新定位中心点。接着，重复以上的操作。

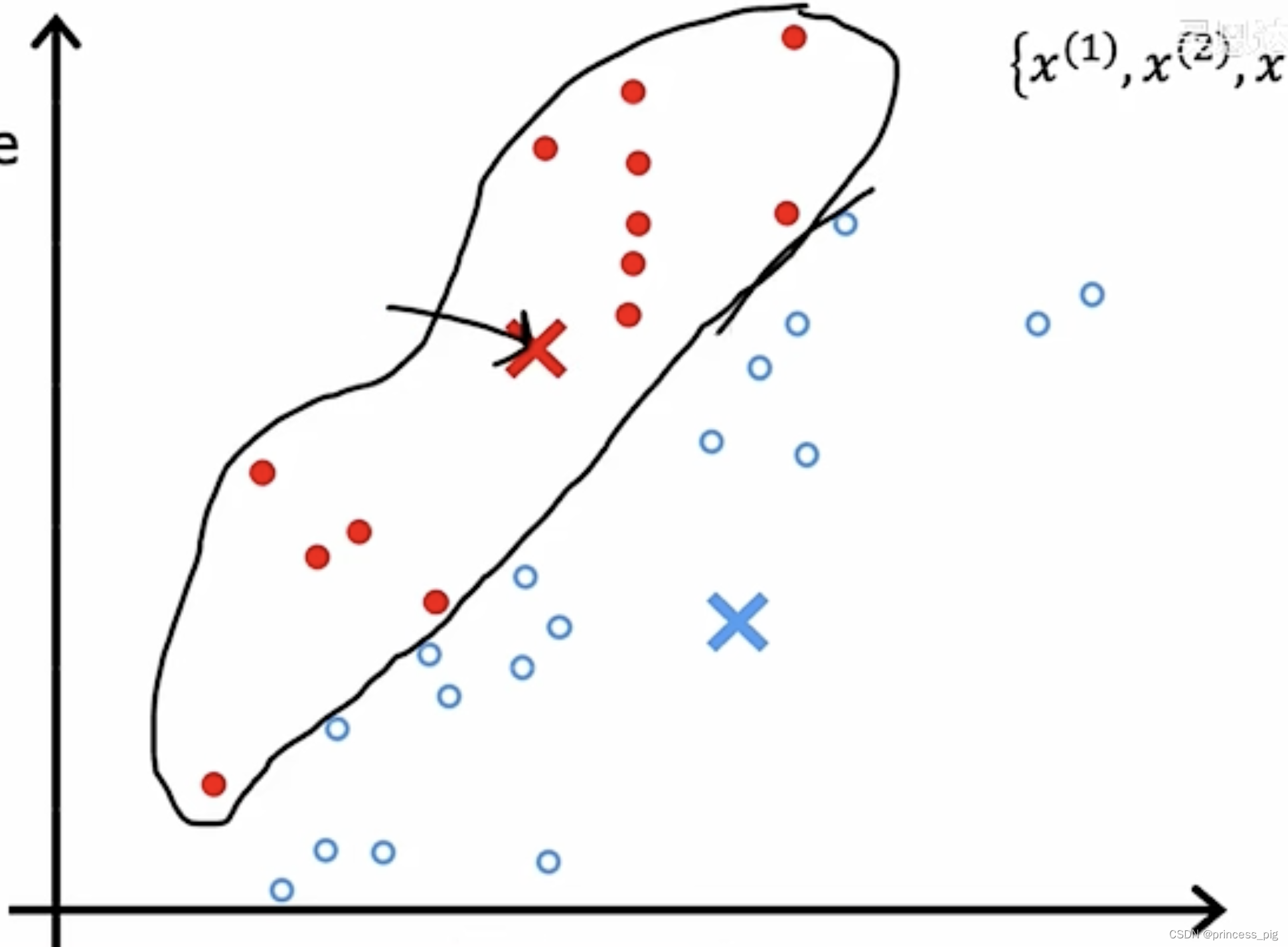
直到我们确定的中心点，不会再产生任何的移动，这时完成了所有的操作。

我们在重新确定中心点时，我们采用的是取它们的坐标的平均值，得到一个新的中心点 。当我们在确定中心点时，我们可以把多出来的那个点去掉，这是一个方法，另外一个方法就是重新我们的确定我们的中心点的操作。

我们根据体重和身高的数值，把我们的数据均分为三个组。这样我们就可以对于不同的人提供不一样大小的T-shirta。

指的是从i=1到k的所有的集群。指的是为k的集群的中心点。指的就是第i个集群的中心点，这时要做优化，就要用到我们的成本函数式子如下,当然我们这里要取得我们的最小值的成本函数。成本函数在这里也可以被称为是失真函数。 

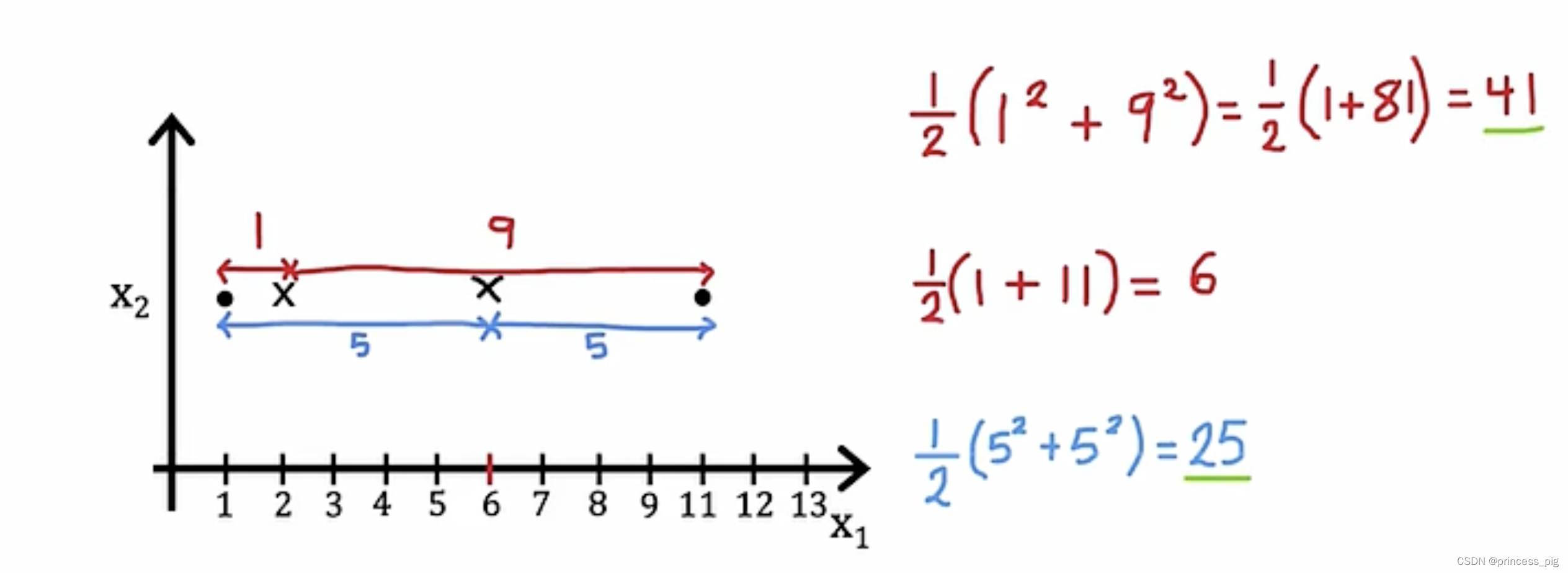
这个图让我们很清晰的看到，在中心点改变时，我们的成本函数明显的变小了，所以说我们的取中心点的操作时正确的，可以让我们找到更加好的中心点。 每一次的迭代，我们的成本函数都会不断的下降，或者保持不变。但如果我们的成本函数发生了上升，那我们的代码中一定出现了bug。

当然，当成本函数不再下降时，那么它已经收敛了，我们需要停止我们的算法。

初始化K-Mean：

K<m，这里的K指的是我们的群集的中心点的个数，m指的是我们的群集点的个数，很明显K<m，但在这里与我们之前不一样的地方在于，之前我们取的是随机点，是在图上的任意点，而我们在这里的初始化的选取中心是从已有的点中选择。

我们会产生多个不同的生成的初始中心，比如下面生成了三个图，我们先计算它们的成本函数，通过成本函数的比较选出我们的成本函数最小的图。J1的值明显远远小于后两个，因为在它之中，每个集群的中心点离集群中的点的距离都非常的小，所以我们就会选择J1的图形。 

我们在这里进行100次的迭代，通过不断的收敛，最后终会得到我们的一个比较小的成本函数值，也就达到了收敛的目标。

选择聚类K的个数： 

如图，我们得到了一幅图，我们要对他们进行分集群，我们每个人有不同的选择。

我们在这里会使用到一个方法：肘方法（elbow method):

集群与成本函数构成的函数的样子和手肘一样，我们可以用这个方法得到每个集群K值与J成本函数有关。 

 在实际情况中，我们并不是用肘方法：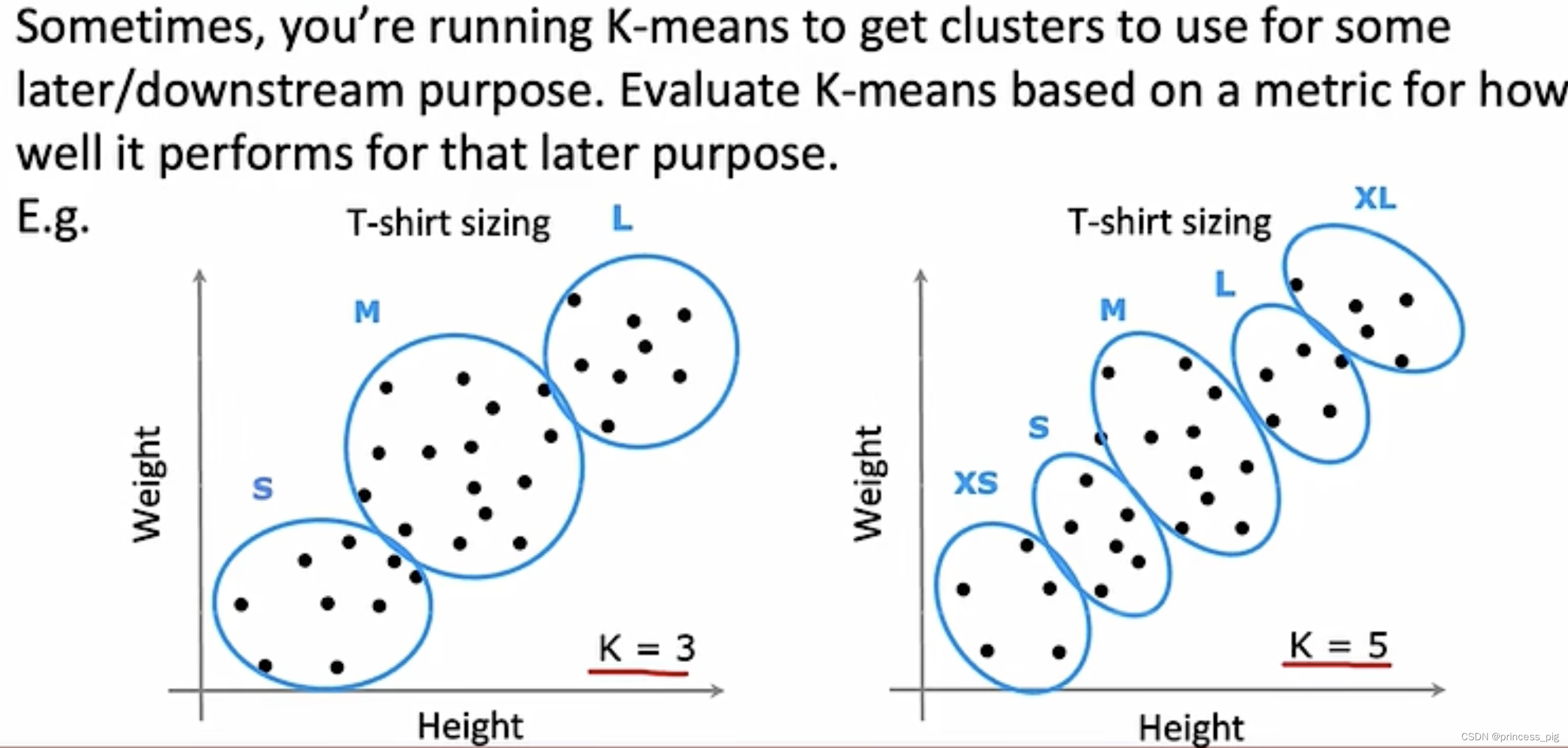

我们要注意的应该是每个不同的集群数量对于后期目标的影响。

我们举一个例子，比如我们的衬衫的尺寸大小 ，我们在第一个图中分为三个尺寸，大中小。第二张图中是超大，大，中，小，超小五个尺寸，我们在这里选择的标准，并不是只是看J成本函数的大小，其中更加重要的是，我们要去注意的这样的设置是否是最优解，对于后期是否好。

这就是第一个无监督算法：聚类算法。