题目链接:D-剪纸游戏_牛客小白月赛86 (nowcoder.com)

题目描述:

输入描述:

输入第一行包含两个空格分隔的整数分别代表 n 和 m。

接下来输入 n行，每行包含 m 个字符，代表残缺纸张。

保证：
1≤n,m≤10001 

字符仅有 '.' 和 '*' 两种字符，其中 '.' 代表被剪去的部分，'*' 代表未被剪去的部分。

实例:

4 10
*.*.*...**
...***.*..
.**..*.*..
*..*****..

输出:

4

案例解释:

分析：

先用dfs或者是bfs探索每一个区域， 看看这个区域里面的时候可以构成一个长方形

注意： 长方形可能是斜着的， 这个是易错点，比如：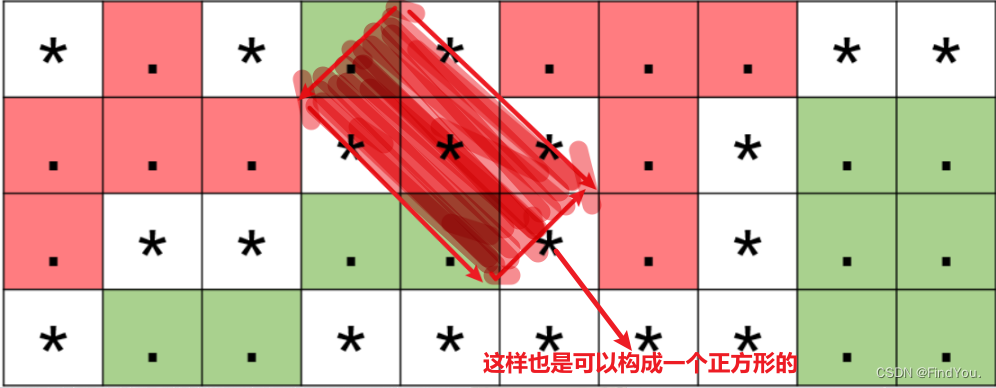

判断正方形：

先求出这一组数据的最左上角(x1, y1) 以及右下角(x2, y2) 统计这个区域里面的个数 num 是否等于(x2 - x1 + 1) * (y2 - y1 + 1); 其实在dfs的时候 就可以进行统计， 引入一个全局变量 x1和y1与当前的dfs遍历的(x, y) x1 = min(x1, x) y1 = min(y1, y) 同理 x2 = max(x2, x) y2 = max(y2, y)

代码：

#include<bits/stdc++.h>
#define y1 Y1
#define fi first
#define endl "\n"
#define se second
#define PI acos(-1)
#define int long long
#define pb(x) push_back(x)
#define PII pair<int, int>
#define Yes cout << "Yes\n";
#define No cout << "No\n";
#define YES cout << "YES\n";
#define NO cout << "NO\n";
#define _for(i, a, b) for(int i = a; i <= b; ++i)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;const int N = 1010;char a[N][N];
bool st[N][N];
int dir[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int n, m, num = 0;int cs = 0, ans = 0;
string s;
//bfs的题目
//dfs也可以
int zsX, zsY, yxX, yxY;bool check(int x, int y) {return x >= 1 && x <= n && y >= 1 && y <= m && !st[x][y] && a[x][y] == '.';
}void dfs(int x, int y) {st[x][y] = true;zsX = min(zsX, x);zsY = min(zsY, y);yxX = max(yxX, x);yxY = max(yxY, y);for(int i = 0; i < 4; ++ i ) {int dx = x + dir[i][0];int dy = y + dir[i][1];if(check(dx, dy)) {num ++ ;st[dx][dy] = 1;dfs(dx, dy);}}
}void bfs(int x, int y) {queue<PII> q;q.push({x, y});while(q.size()) {auto p = q.front();q.pop();for(int i = 0; i < 4; ++ i ) {int dx = p.fi + dir[i][0];int dy = p.se + dir[i][1];if(check(dx, dy)) {st[dx][dy] = 1;q.push({dx, dy});}}}
}signed main() {IOS;cin >> n >> m;_for(i, 1, n) {_for(j, 1, m) {cin >> a[i][j];}}_for(i, 1, n) {_for(j, 1, m) {if(check(i, j)) {//	cout << "i = " << i << " j = " << j << endl;num = 1;zsX = 1010; //最左边的 zsY = 1010;yxX = 0;yxY = 0; // 最右边的 st[i][j] = true;dfs(i, j);
//				cout << "num = " << num << endl;
//				cout << "zsX = " << zsX << " zsY = " << zsY << " yxX = " << yxX << " yxY = " << yxY << endl; if(num == (yxX - zsX + 1) * (yxY - zsY + 1)) {ans ++ ; }}}}cout << ans << endl;return 0;
}