作者:丁点helper
来源:丁点帮你
前几天的文章,我们聚焦在回归分析,今天来看看在回归分析中常常要研究的一类难点问题——交互作用的探究。
交互(interaction),字面上不太好理解,但是从数学表达上却很简单。
如果想要研究两个自变量如X1和X2的交互作用,通常的做法就是将两个变量相乘,即X1*X2,然后把乘积项纳入到回归方程。
操作起来很简单,但交互项的纳入对于回归系数的解读却带来了新的问题。
以一个很经典的例子来说明。
含交互项的回归方程
多重线性回归,一般是指有多个自变量X,只有一个因变量Y。前面我们主要是以简单线性回归为例在介绍,两者的差距主要在于自变量X的数量,在只有一个X时,就称简单线性回归。
我们想通过线性回归研究教育程度、性别对个人收入的影响,首先,不纳入交互项的回归方程为:
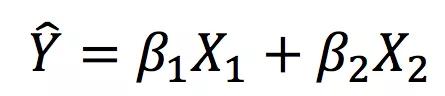
其中,Y表示收入,X1表示“教育年限”(定量变量),X2表示“性别”(分类变量,用”0“为女性;“1“表示男性)。
通过估计以上回归方程X1和X2的回归系数,β1和β2,即可定量地衡量出教育程度、性别对收入的影响。
比如,β1的含义即为:控制性别后,教育程度每增加一年,个人收入增加的量。
这是我们前面讲过的,很好理解。
现在,我们希望考虑”教育程度“和”性别“的交互作用,因此将把两个变量的交互项纳入回归方程,即为:
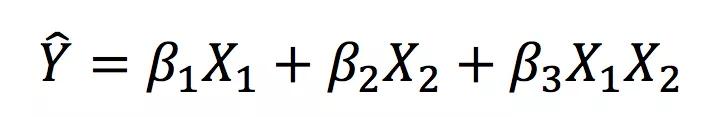
其中,X1X2代表交互项,这里也属于多重线性回归的范畴,因为我们可以令X3=X1X2,将其视为一个新变量,则上式就可以看做是拥有三个自变量的一般线性回归。
思考:现在方程中X1的回归系数β1还能按照上面的含义来解读吗?
我们尝试做一下。
要衡量X1对Y的作用,归根结底,是要看,当X1变化一个单位时,Y怎么变化(明白这一点很基础也很重要)。
因此,我们可以这样来做:
当X1=0时(代入有交互项的方程,下同),

由此,可以发现,加入交互项后,X1(即教育程度),每变化一个单位(比如增加一年),收入的变化不仅取决于β1,而且还取决于β3和X2。
因此,我们不能再直接将β1解读为教育程度对收入的影响。
同理,β2也不能直接解读为性别对收入的影响。
在这样的情况下,到底应该如何来对这三个回归系数进行解读呢?思路其实很简单,诀窍就是分别让X1和X2等于0。

由此来看,加入交互作用后,回归系数(β1和β2)的解读需要加入一定的限定条件,比如”教育程度为0“、或者特定为“女性人群“。
这实际上是出于简单的数学考虑:因为让一个变量等于0,我们就可以消除交互项,然后单独地分析另一个变量的效应,这种思路特别方便,大家不妨在自己的研究中使用。
说完β1和β2,那β3怎么解读呢?严格而言,β3才是真正交互项的系数,才是做交互研究最关注的部分。
交互项回归系数的解读
多重线性回归,一般是指有多个自变量X,只有一个因变量Y。前面我们主要是以简单线性回归为例在介绍,两者的差距主要在于自变量X的数量,在只有一个X时,就称简单线性回归。
上面我们讲了β1的含义是”对于女性人群,教育程度每增加一年,其收入的增加量“。很自然的想,那对于男性人群,教育每增加一年,收入增加多少呢?
前面我们计算了,X1从0变化到1时,
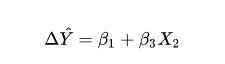
我们知道,X2表示的是性别这个变量,X2=1代表男性,那如果我们直接把X2=1代入上式呢:
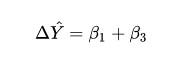
由此,我们就得到了:对于X2=1(即男性人群),当X1增加一个单位时,Y的变化量为(β1 + β3)。
因此,可以把(β1 + β3)解读为:对于男性人群,教育程度每增加一年,收入的增加量。
把男性和女性放在一起对照看一下:
β1:对于女性人群,教育程度每增加一年,其收入的增加量。
β1 + β3:对于男性人群,教育程度每增加一年,其收入的增加量。
现在,β3(即交互项的回归系数)的含义是不是一目了然。它表示,教育程度每增加一年时,男性和女性收入增加的差值。
代入具体的数字看起来会更容易。
比如,我们让β1 = 200;β2 = 300;β3 = 50,就可以很清楚地看到:
对于女性来讲,教育程度每增加一年,收入会增加200(β1 的含义);
对于男性来讲,教育程度每增加一年,收入会增加250(β1 + β3的含义)。
而β3就表示,同样增加一年的教育程度,收入的增加量,男性比女性多50。
这多出来的50就衡量了性别和教育的交互作用。
理清了这三个系数的意义,我们再来看交互作用的真正含义,就会更加明朗:
交互作用实际上影响的是一种关系,什么关系?X1和Y的关系,或者X2和Y的关系。
此话怎讲?我们看,当不加入交互项的时候,无论男性还是女性,教育程度增加一年,收入的增加量是一样的,都为β1。
这里的β1 可以视作教育程度对收入的影响,实际上是两者相关关系的量化。
但是,加入交互作用后,教育程度增加一年,收入的增加量,男性和女性就不一样了,一个是β1 + β3,另一个是β1。
不难发现,教育程度对收入的影响随着性别的变化发生了变化。
所以,从本质上看,交互项衡量的了性别对【教育程度与收入关系】的影响。用括号括起来就是希望大家能看的更清楚:性别和教育的交互项影响的既不是教育程度也不是收入,而是它们两者的关系。
如果数学基础不错,则可以将“【教育程度与收入关系】”理解为回归方程的X1(教育程度)的斜率(斜率的定义就是X1变化一个单位,对应的Y的变化量),所以,本质上,交互项影响的是斜率!
同样地,交互项因为是乘积的形式,所以它也衡量了教育程度对(性别与收入关系)的影响。
如何进行分析,做法其实完全一致,首先分别计算X2=0和X2=1时候,Y的变化量(代表了男女收入的差异):
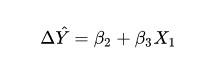
我们知道X2表示性别,所以,根据上式,可以将β3解读为:教育程度的变化,带来的男女收入水平差异的变化,注意这里说的是”差异“,即男性工资高于女性的那一部分(如果β3是负数,则表示男性工资更低)。
因此,综合来看,交互项是可以从两个角度去理解和解读的,这符合它进入回归方程的方式(X1X2)。
针对具体的问题,我们都可以采取上面说的这种”归零法“去分析和拆解,即分别一个自变量等于0,然后分析另一个自变量回归系数的含义。
同时,专门对于交互项的解读,我们要知道它刻画的其实是对回归斜率或者回归效应值(β)的影响。
比如教育程度和性别的交互,既影响了收入对教育程度的斜率,也影响了收入对性别的斜率。