回调函数是什么?
回调函数就是⼀个通过函数指针调⽤的函数。
如果你把函数的指针(地址)作为参数传递给另⼀个函数,当这个指针被⽤来调⽤其所指向的函数
时,被调⽤的函数就是回调函数。回调函数不是由该函数的实现⽅直接调⽤,⽽是在特定的事件或条件发⽣时由另外的⼀⽅调⽤的,⽤于对该事件或条件进⾏响应。
在函数指针数组及转移表: http://t.csdnimg.cn/BBvjE
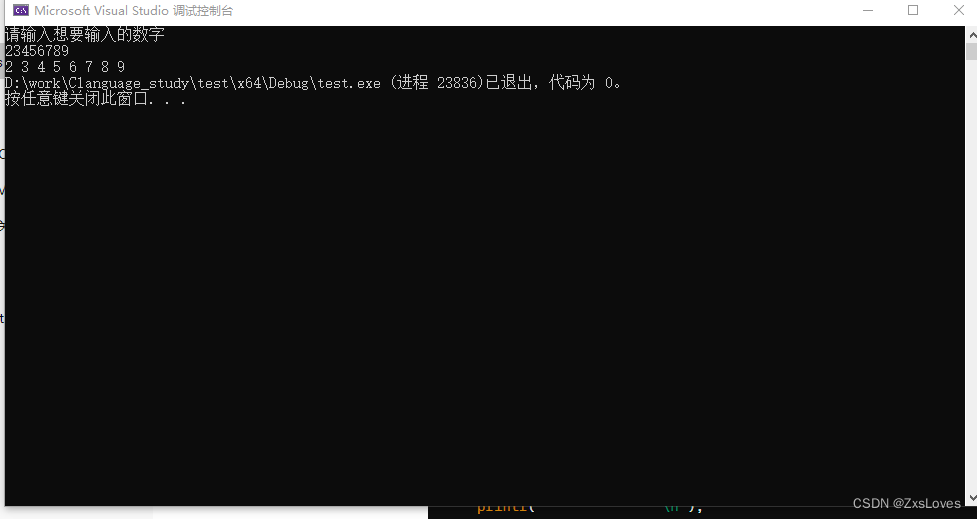
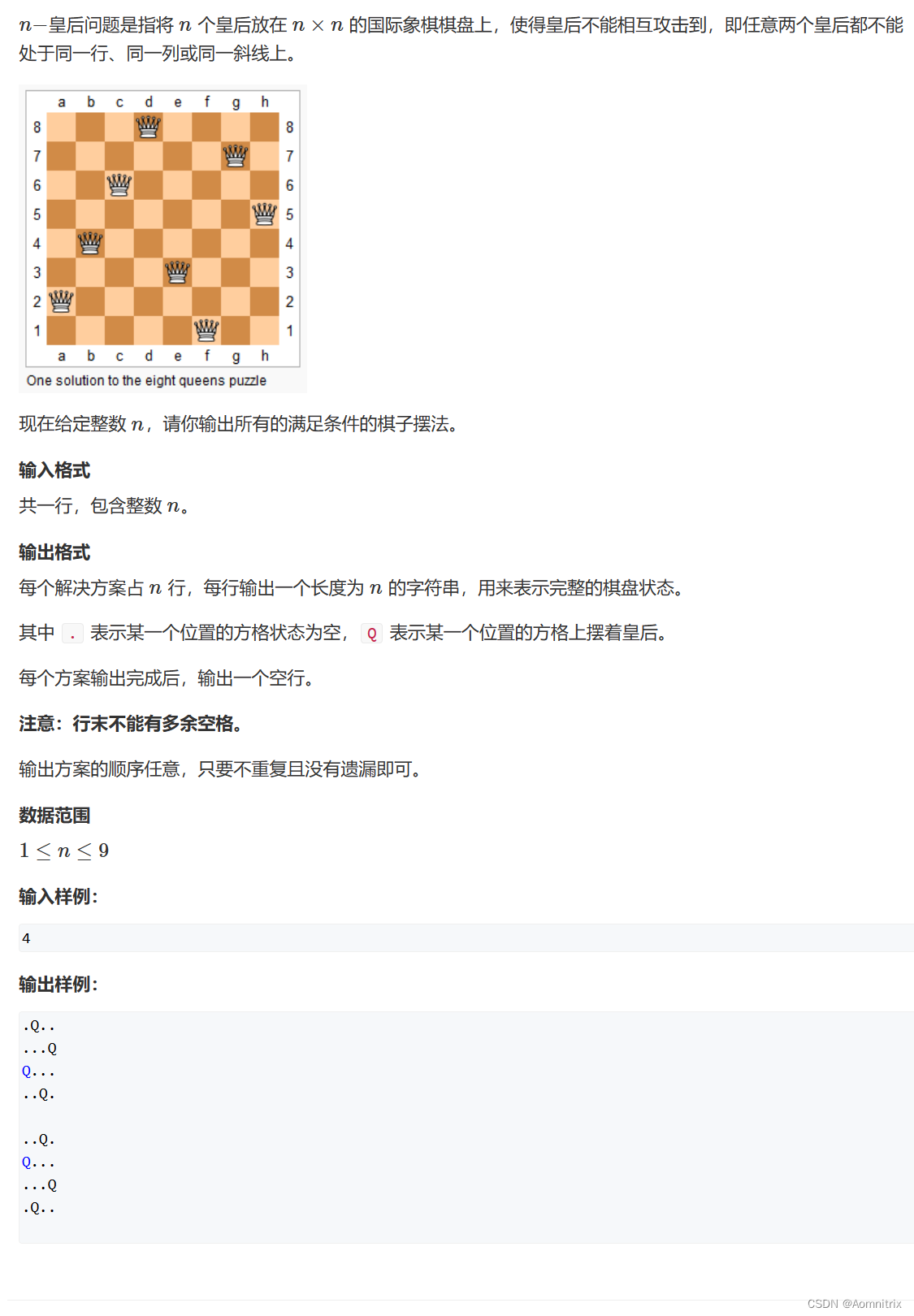
我们写的计算机的实现的代码中,有一部分重复出现的,在这里我也复制过来:

其中虽然执⾏计算的逻辑是区别的,但是输⼊输出操作是冗余的,有没有办法,简化⼀些呢?
因为红笔圈住的代码,只有调⽤函数的逻辑是有差异的,我们可以把调⽤的函数的地址以参数的形式 传递过去,使⽤函数指针接收,函数指针指向什么函数就调⽤什么函数,这⾥其实使⽤的就是回调函数的功能。
在这里我们用回调函数的知识来优化一下代码,在扇面连接中有我们优化这段代码的另一种方式,利用函数指针数组,这里关于这种方法不再赘述。
下面我们看一下用回调函数优化后的代码:
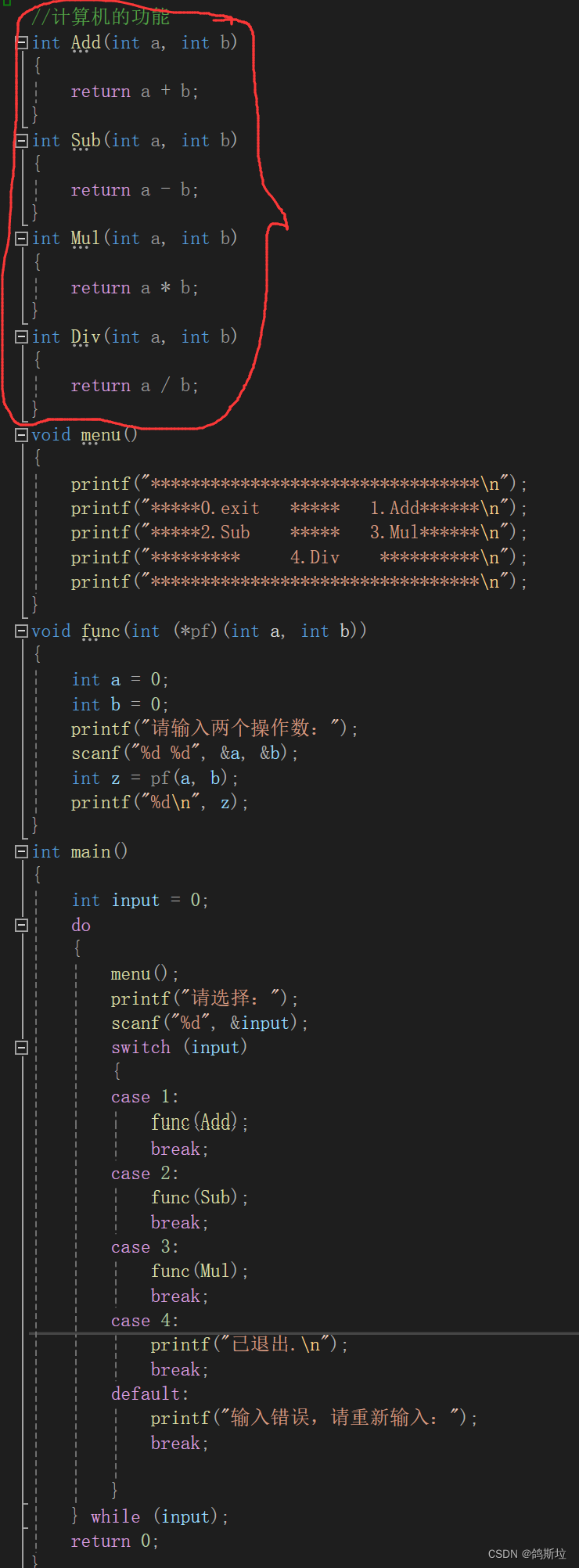
圈住的函数没有在主函数中调用,是将函数作为指针传给另一个函数,在这个函数中调用圈住的函数,,圈住的函数就叫做回调函数。
接下来我们要利用回调函数,模拟qsort的功能,尽情期待。。。
感谢观看,感谢指正