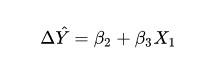多元线性回归分析（Stata）

一、回归分析的介绍与分类

二、多元线性回归模型的条件

1. 线性理解与内生性问题研究

2. 异方差问题

3. 多重共线性问题

一、回归分析的介绍与分类

回归分析的任务是：通过研究自变量X和因变量Y的关系，尝试去解释Y的形成机制，进而达到通过X去预测Y的目的

三个关键字：相关性、因变量Y、自变量X

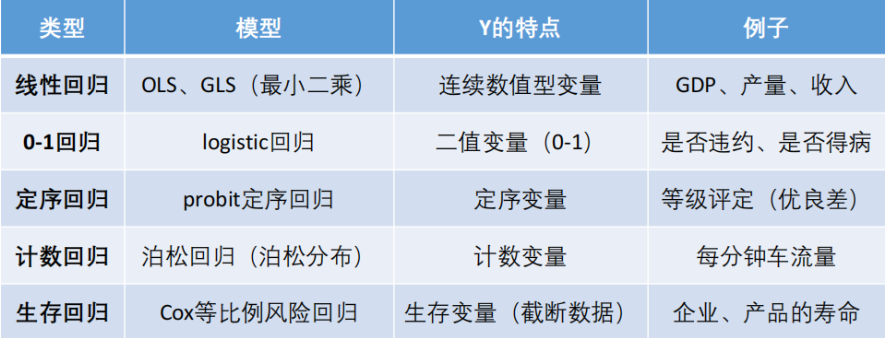
常见的回归分析有五类（划分的依据是因变量Y的类型）：

线性回归：因变量Y为连续性数值变量，例如GDP的增长率
0-1回归：因变量Y为0-1型变量，例如P2P公司研究借款人是否能按时还贷，那么Y可以设计为二值变量，Y=0时代表可以还贷，Y=1时代表不能还贷
定序回归：因变量Y为定序变量 ，例如1表示不喜欢，2表示一般般，3表示喜欢
计数回归：因变量Y为计数变量，例如管理学中的RFM模型，F代表一定时间内，客户到访的次数，次数其实就是一个非负整数
生存回归：因变量Y为生存变量（截断数据），例如研究产品寿命，企业寿命和人的寿命，假设做吸烟对寿命的影响，选取的样本中老王60岁，但是老王此时身体很健康，不能等老王去世再做研究，所以只能记他的寿命为60+，这种数据就是截断的数据

回归分析的使命：

识别重要变量，那些自变量X是同Y真的相关
判断相关性的方向，正相关还是反相关
要估计权重

回归分析的分类

数据的分类

横截面数据：在某一时点收集的不同对象的数据，eg：全国各省份2021年GDP数据
时间序列数据：在同一对象在不同时间连续观察所得的数据，eg：某地方每隔一小时测得的温度数据
面板数据：横截面数据和时间序列数据综合在一起的一种数据

二、多元线性回归模型的条件

模型符合线性模式
X满秩（无多重共线性）
零均值价值 E(ξi∣Xi)=0 （自变量外生）无内生性问题
同方差：Var(ξi∣Xi)=σ
无自相关：Cov(ξi,Xi)=0

1. 线性理解与内生性问题研究

回归分析中对线性的理解

回归分析中的线性假定并不要求初始模型都呈严格的线性关系，自变量和因变量可以通过变量替换来转换成线性模型

例如：

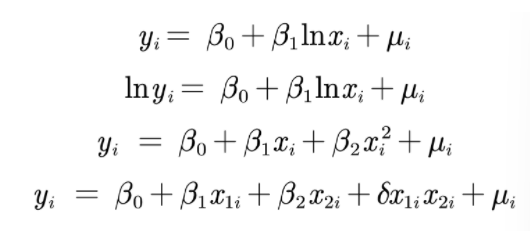
标准化回归系数

我们通常得到的回归方程中的回归系数都是非标准化回归系数，表示的是在其他自变量不变的时候，该系数对应的自变量每增加一个单位的量，因变量就增加该系数的值，体现的是对因变量绝对的影响，并不能去判断不同自变量之间谁对因变量的影响大；而标准化回归系数就是指对数据进行标准化处理

标准化处理：讲原始数据减去它的均数后除以它的标准差，计算得到新的变量值，消除了量纲、数量级等差异的影响

标准化处理后得到的回归方程即为标准化回归方程，使得不同变量间具有可变性，标准回归系数的绝对值越大即对因变量的影响最大（只关注显著的回归系数）

stata操作：在regress 后添加参数b

regress y x1 x2 ... xk, b

对数据进行描述性统计的方法

excel数据分析
stata-summarize

Stata工具的使用

数据的描述性统计
- 定量数据：summarize 变量1 变量2 ...
- 定性数据：tabulate 变量名, (gen(A))
  
  返回对应这个变量的频率分布表，可选择并生成对应的虚拟变量（以A开头）
  
  虚拟变量是针对定性数据而设置的特殊变量详细解释看Chapter7

回归分析

regression y x1 x2 ... xk（默认采用的是OLS普通最小二乘法）

利用Stata对数据进行回归分析的注意点

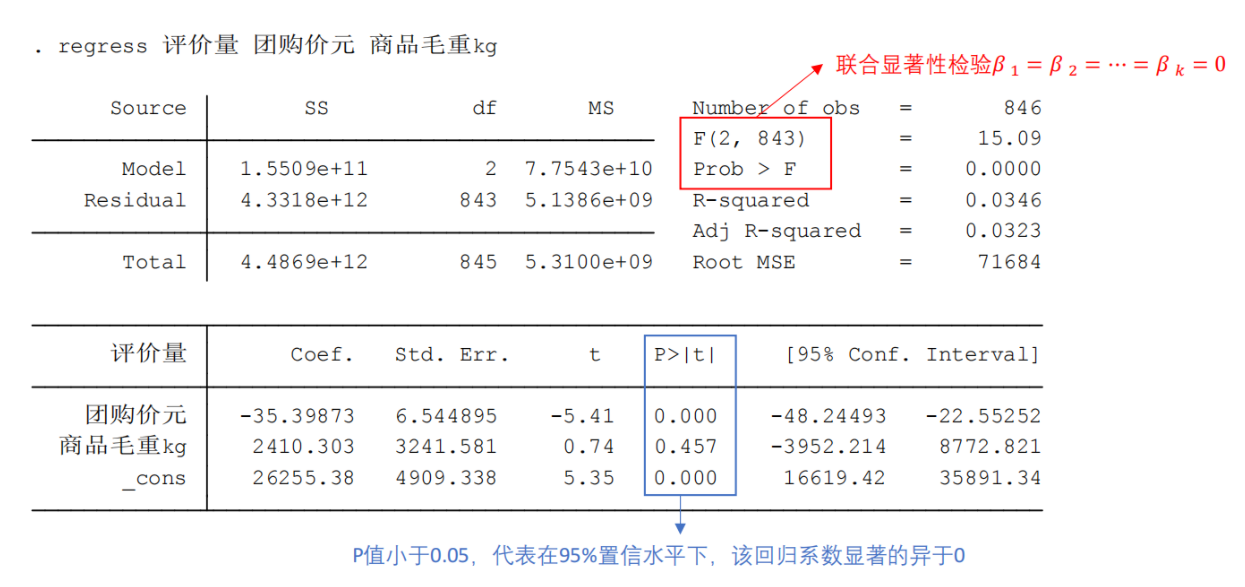
解释：

上表格第一行依次为SS（sum of squares），df（degree of freedom），MS（mean square）
右边的F(df of model, df of residual) = MS of Model / MS of Residual = 7.7543e+10/5.1386e+9 = 15.09
F值的H0假设是：所有的自变量predictor都对y不会产生影响，即所有predictor的coef都=0，所有的predictor都不significant
下面的prob > F是指上述H0成立的可能性。当其趋于0时表示至少会有一些predictor的coef不为0（即相关）——模型合理
Adj R-squared 由于R2存在一个问题：无论什么predictor加到模型中，R2都会变大。为了避免这个问题，adjR2惩罚了模型的复杂度
下面这张表格的第一列为coef回归系数
第二列为Coef的Std.Err，值越小说明Coef的值越可信
第三列t值=Coef / Std.Err，|t-statistics| > 2对应的predictor就是significant
第三列是p > |t|，表示prob > |t|，值小于0.05一般就是significant

核心关注点：

模型是否合理：联合显著性检验，如果P值<0.05说明存在相关性，否则不存在

置信度高低（系数显著与否）：如果P值（蓝色）<0.1说明置信度>90%，<0.05说明置信度大于95%，Regession coeffient显著

2. 异方差问题

第一张为同方差：生成的线性模型到每个数据的垂直水平距离相差无几就是同方差；后面三张即为不同类型的异方差

异方差的检验

残差图检验（应该是稳定的平行于X轴） Stata中的操作：
- rvfplot （画残差与拟合值的散点图）
- rvpplot x （画残差与自变量X的散点图）
怀特检验（white检验） Stata中的操作：
```
estat imtest, white
```

怀特检验的原假设：不存在异方差若p值<0.05说明在置信度95%以上认为原假设不成立

异方差的纠正

OLS+稳健的标准差

如果发现存在异方差，一种处理方法是，仍然进行OLS 回归，但使用稳健标准误。这是最简单，也是目前通用的方法。只要样本容量较大，即使在异方差的情况下，若使用稳健标准误，则所有参数估计、假设检验均可照常进行。换言之，只要使用了稳健标准误，就可以与异方差“和平共处”了。

Stata的操作：
```
regress y x1 x2 ... xk, robust
```
广义最小二乘法GLS

Stock and Watson (2011)推荐，在大多数情况下应该使用“OLS + 稳健标准误”

3. 多重共线性问题

表现:

系数估计值符号相反
某些重要的解释变量t值低但是R2不低
当一不太重要的解释变量被删除后，回归结果显著变化

原因：

某一解释遍历可以由其他解释变量线性表示
解释变量享有共同的时间趋势
由于数据收集的基础不够宽，某些解释变量可能会一起变动
一个解释变量是另一个的滞后，二者往往遵循一个趋势

检验（VIF）

Stata操作：

estat vif

Soution

逐步回归分析

较好在生成线性模型时就能避免多重共线性问题

向前逐步回归Forward selection：将自变量逐个引入模型，每引入一个后都要进行检验，显著时才加入回归模型
缺点：随着以后的自变量的引入，原来显著的自变量也可能变成不显著
向后逐步回归Backward elimination：与向前逐步回归相反，先将所有自变量添加，之后一个个地尝试将自变量从模型中剔除，看整个模型解释因变量的变异是否有显著变化，之后将最没有解释力的剔除，不断迭代，直到没有需要被剔除的

Stata操作：

Forward selection: