数据挖掘与分析学习笔记

一、Numpy

NumPy（Numerical Python）是一种开源的Python库，专注于数值计算和处理多维数组。它是Python数据科学和机器学习生态系统的基础工具包之一，因为它高效地实现了向量化计算，并提供了对大型多维数组和矩阵的支持。

NumPy的定义要点：

核心对象：NumPy中最关键的对象是ndarray（n-dimensional array object），即N维数组，这是一种高效存储同构数据（所有元素类型相同的多维数组）的数据结构，适合进行大规模数值计算。
高效内存管理：ndarrays以一种连续的内存布局存储数据，使得CPU缓存利用更高效，从而加速了数学和逻辑运算。
数学函数库：NumPy包含了大量数学函数，这些函数可以直接作用于整个数组，无需使用循环，提高了执行效率。
广播功能：NumPy支持广播机制，允许不同形状的数组之间进行运算，自动进行元素级的逐点运算。
兼容性：NumPy与C/C++和Fortran编写的代码高度兼容，可以通过NumPy的C API集成其他高性能库。

使用领域：

数据分析：在数据预处理阶段，NumPy被广泛用于数据清洗、转换、统计分析等任务。
机器学习：作为大多数深度学习和机器学习框架（例如TensorFlow、PyTorch）的基础组件，NumPy提供的数组处理能力对于构建和训练模型至关重要。
信号处理与图像处理：NumPy能够便捷地处理图像和信号数据，支持矩阵运算和快速傅里叶变换等算法。
科学计算：包括物理模拟、工程计算、金融建模等领域，NumPy的高效数组运算和内置的线性代数功能十分有用。
大数据处理：虽然不是专门的大数据工具，但NumPy数组结合Pandas等库，可在单机环境下处理大规模数据集。

总之，NumPy因其高效性和灵活性成为了众多Python开发者在涉及数值计算、科学计算及数据分析项目时首选的库。

1.赋值定义较复杂数据结构

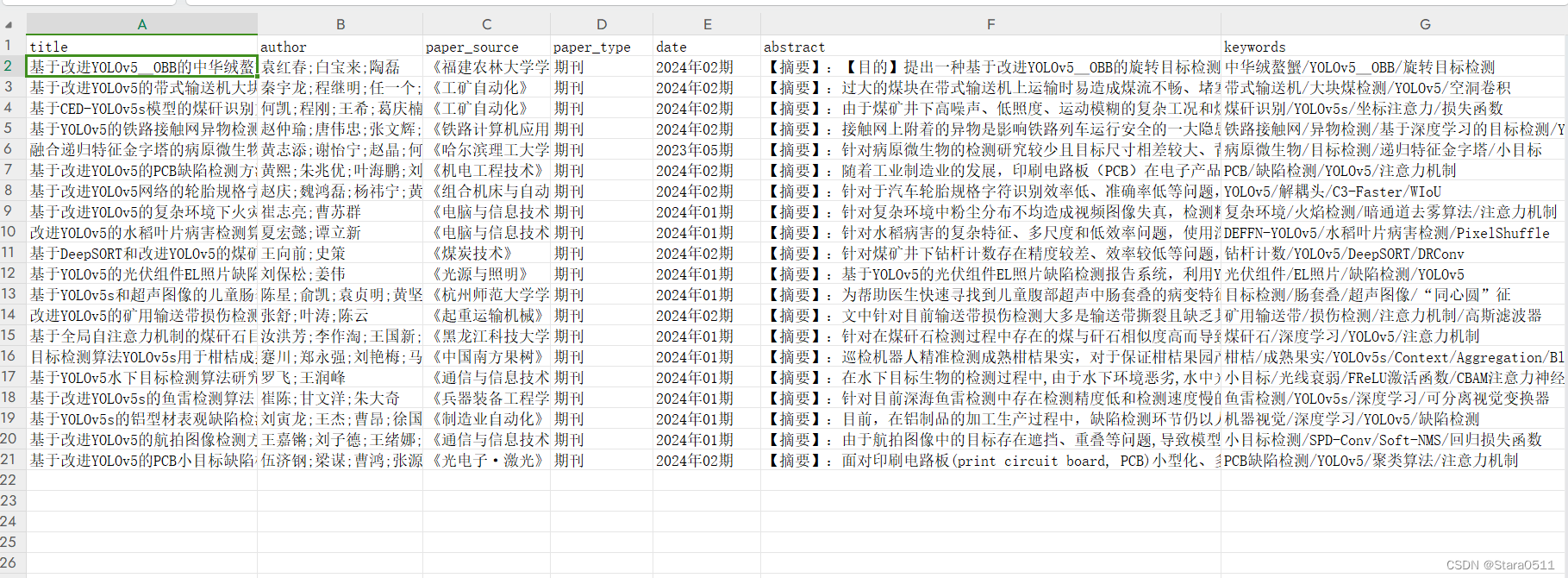
对比Python的基本数据类型（列表、元组、字典等），数组具有更灵活的数据存储方式，比如一维数组和二维数组或者矩阵，特别是对于数值型数据来说更有优势，根据给出的列表L1=[1,2,3,4,0.1,7]和嵌套列表L2= [[1,2,3,4],(5,6,7,8)]，请利用numpy包中的array()函数将其定义为一维数组和二维数据。

相关代码

import numpy as np
# 给定的列表
L1 = [1, 2, 3, 4, 0.1, 7]
L2 = [[1, 2, 3, 4], (5, 6, 7, 8)]
# 创建一维数组
array_1d = np.array(L1)
print("一维数组:")
print(array_1d)
# 创建二维数组（或矩阵）
# 注意：L2中的元组会被自动转换为列表，因为numpy数组要求元素类型一致
array_2d = np.array(L2)
print("二维数组:")
print(array_2d)

运行结果

2.内嵌函数定义较复杂数据结构

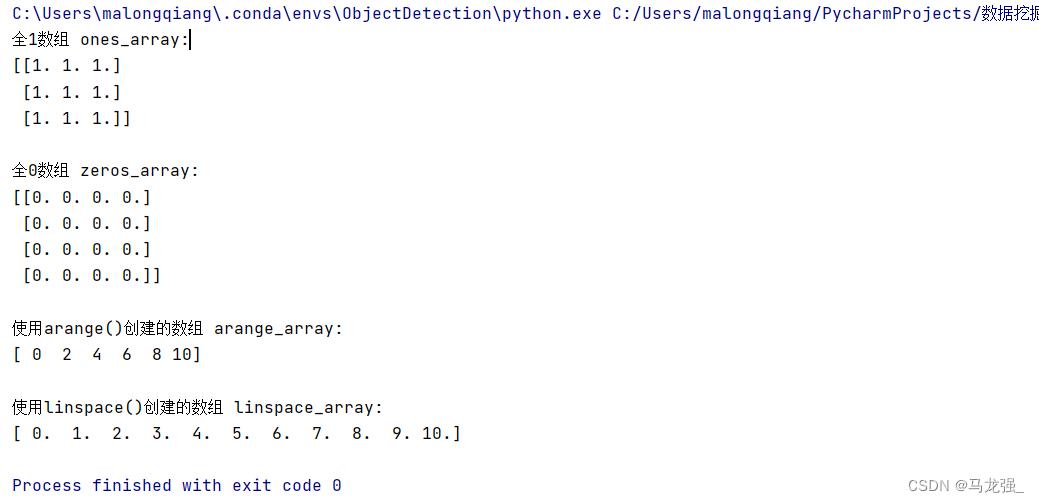
在编程过程中，预先定义一些数组变量用来保存程序产生的结果是非常必要的，请分别给出利用numpy包中ones ()、zeros()、arange()、linspace()函数定义的例子。

相关代码

import numpy as np
# 使用ones()创建一个3x3的全1数组
ones_array = np.ones((3, 3))
# 使用zeros()创建一个4x4的全0数组
zeros_array = np.zeros((4, 4))
# 使用arange()创建一个从0到10的整数数组，步长为2
arange_array = np.arange(0, 11, 2)
# 使用linspace()创建一个从0到10的等差数列，包含11个元素
linspace_array = np.linspace(0, 10, 11)
# 输出结果
print("全1数组 ones_array:")
print(ones_array)
print("\n全0数组 zeros_array:")
print(zeros_array)
print("\n使用arange()创建的数组 arange_array:")
print(arange_array)
print("\n使用linspace()创建的数组 linspace_array:")
print(linspace_array)

运行结果

3.数组运算

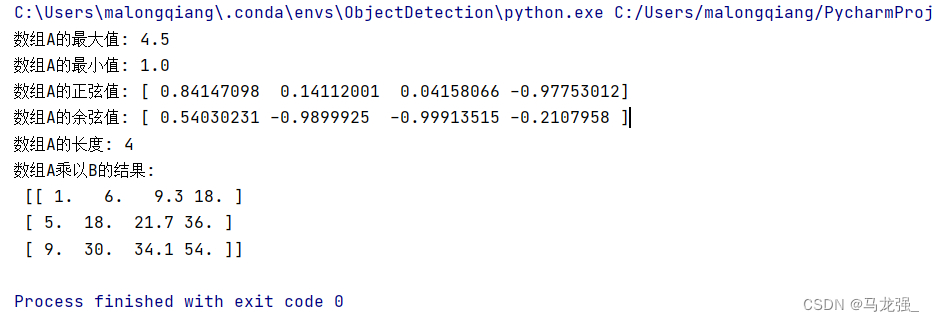
现有数组A=np.array([1,3,3.1,4.5])和B=np.array( [[1,2,3,4],(5,6,7,8),[9,10,11,12]])，请求解出A的最大值、最小值、正弦值、余弦值、长度和A乘B的程序。

相关代码

import numpy as np
# 定义数组A和B
A = np.array([1, 3, 3.1, 4.5])
B = np.array([[1, 2, 3, 4], (5, 6, 7, 8), [9, 10, 11, 12]])
# 计算A的最大值
max_A = np.max(A)
# 计算A的最小值
min_A = np.min(A)
# 计算A的正弦值
sin_A = np.sin(A)
# 计算A的余弦值
cos_A = np.cos(A)
# 计算A的长度
length_A = len(A)
# 计算A乘B
multi =A * B
# 输出结果
print("数组A的最大值:", max_A)
print("数组A的最小值:", min_A)
print("数组A的正弦值:", sin_A)
print("数组A的余弦值:", cos_A)
print("数组A的长度:", length_A)
print("数组A乘以B的结果:\n", multi)

运行结果

4.数组切片

现有数组A=np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]])，编程实现如下功能：

1）将6、7、14、16这四个元素顺序切片出来构成一个2*2数组；

2）取第0列元素小于9的第2、3列数据，并赋值给B。

相关代码

import numpy as np
# 创建一个4x4的数组A
A = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]])
# 从数组A中选取第1行第1列、第1行第2列、第3行第1列和第3行第3列的元素
# 然后将其重塑为2x2的数组A_
A_ = np.array([A[1,1],A[1,2],A[3,1],A[3,3]]).reshape(2,2)
# 从数组A中选取第0列元素小于9的行，然后选取第2列和第3列的数据
B = A[A[:,0] < 9, [2,3]]
# 打印原始数组A
print(A)
# 打印重塑后的数组A_
print(A_)
# 打印数组B
print(B)

运行结果

5.数组连接

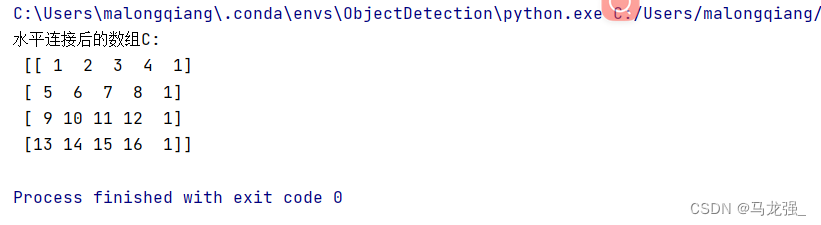
现有数组A=np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]])和B= np.array([1,1,1,1])，请将数组A和数组B进行水平连接获得新数组C，即C的前4列来源于A，最后一列来源于B。

相关代码

import numpy as np
# 定义数组A和B
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16]])
B = np.array([1, 1, 1, 1])
# 将数组A和数组B水平连接，得到新数组C
C = np.column_stack((A, B))
# 输出结果
print("水平连接后的数组C:\n", C)

运行结果

二、Pandas

Pandas 是一个开源的 Python 库，专门为数据分析和处理而设计，它在数据科学、统计学和机器学习等领域具有广泛应用。Pandas 建立在 NumPy 数值计算库的基础上，为 Python 提供了高性能、易用且功能丰富的数据结构和数据分析工具。

Pandas 的定义要点：

数据结构：Pandas 主要引入了两种核心数据结构：
- Series：一维数组，带标签的有序数据集，可以存储任意数据类型。
- DataFrame：二维表格型数据结构，包含行和列索引，每一列可以是不同的数据类型，类似于关系型数据库中的表或电子表格。
数据处理能力：Pandas 提供了一系列强大的数据清洗、整合、重塑、过滤、分组、排序、统计分析等功能。
I/O 功能：能够方便地从不同数据源（如CSV、Excel、SQL数据库、HDF5、JSON等）读取数据，并将数据写回上述格式或其他格式。
时间序列功能：特别擅长处理时间序列数据，拥有丰富的时间序列分析工具，如日期范围生成、频率转换、移动窗口统计等。
集成性：Pandas 良好的兼容性和集成性使其能无缝衔接其他 Python 库，如 matplotlib 用于可视化、NumPy 用于数值计算、SciPy 用于科学计算、Statsmodels 用于统计建模、Scikit-learn 用于机器学习等。

Pandas 的使用领域：

数据分析：Pandas 在商业智能和数据分析中广泛用于数据探索、数据质量评估、数据预处理等步骤，帮助数据分析师快速理解数据分布、查找模式和异常。
数据清洗和整理：Pandas 提供了一系列方法用于处理缺失值、重复值、异常值，以及数据类型转换、重命名、合并、切片、拼接等数据预处理工作。
统计分析：支持复杂的数据聚合、分组运算、描述性统计分析，以及更深入的统计检验和模型拟合前的数据准备。
机器学习和人工智能：在机器学习项目中，Pandas 是数据预处理阶段不可或缺的一部分，用于特征工程、特征选择和数据分割等任务。
商业和科学研究：在各行各业的数据密集型工作中，包括但不限于金融、医疗、市场营销、社会科学研究等，Pandas 都是进行高效数据处理和分析的关键工具。

1.序列和数据框

现有列表L1=[1,-2,2.3,'hq']、L2=[‘kl’,’ht’,’as’,’km’]和元组T1=(1,8,8,9)和T2=(2,4,7,’hp’)

1）请给出值为L1，采用默认索引和指定索引（’a’,’b’,’c’,’d’）两种方式的序列定义方法。

相关代码

import pandas as pd
L1 = [1, -2, 2.3, 'hq']
series_default_index = pd.Series(L1)
print("序列（默认索引）:")
print(series_default_index)

import pandas as pd
L1 = [1, -2, 2.3, 'hq']
index_labels = ['a', 'b', 'c', 'd']
series_specified_index = pd.Series(L1, index=index_labels)
print("序列（指定索引）:")
print(series_specified_index)

运行结果

2）请给出索引为’a’,’b’,’c’,’d’，列名和值分别为’L1’ ,’L2’ ,’T1’ ,’T2’及其值的数据框构造方法。

相关代码

import pandas as pdL1 = [1, -2, 2.3, 'hq']
L2 = ['kl', 'ht', 'as', 'km']
T1 = (1, 8, 8, 9)
T2 = (2, 4, 7, 'hp')# 为了创建一个DataFrame，我们需要一个列表的列表或者字典，其中键是列名
data = {'L1': L1,'L2': L2,'T1': list(T1),  # 将元组转换为列表'T2': list(T2)  # 将元组转换为列表
}# 构造数据框，并指定索引
df = pd.DataFrame(data, index=['a', 'b', 'c', 'd'])
print("数据框:")
print(df)

运行结果

2.外部数据文件读取

1）请读取“一、车次上车人数统计表.xlsx”中的sheet2数据，用一个数据框df1来表示；

相关代码

import pandas as pd
# 1）读取Excel文件中的sheet2数据
file_path_excel = "一、车次上车人数统计表.xlsx"
sheet_name = "Sheet2"
df1 = pd.read_excel(file_path_excel, sheet_name=sheet_name)
print(df1)

运行结果

2）请读取文本文件txt1中的数据，用一个数据框df2来表示；

相关代码

import pandas as pd
file_path_txt = "txt1.txt"
df2 = pd.read_csv(file_path_txt, sep="\t")  # 假设文本文件使用制表符分隔
print(df2)

运行结果

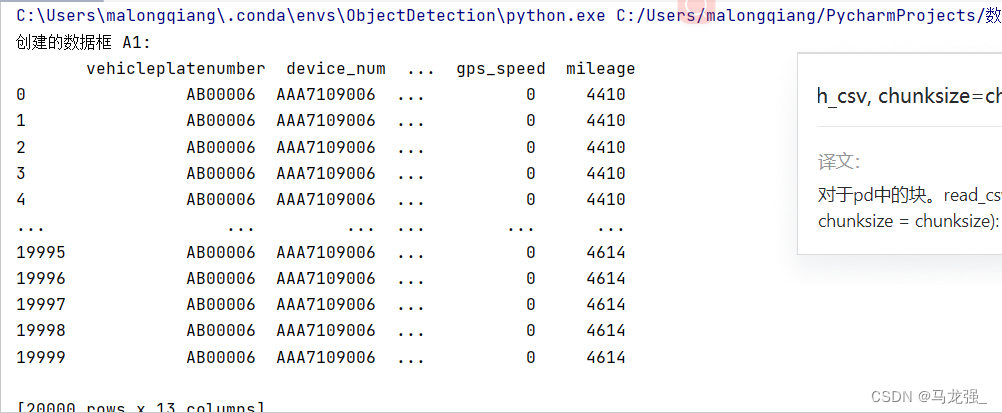
3）大容量文件的读取需要采用分块读取的方式来处理数据，比如csv文件常用来存放大容量文件。请采用分块读取的方式读取“data.csv”文件，每次读取20000行，读取出来的数据分别用数据框A1，A2，A3，A4……等来表示。

相关代码

import pandas as pd
file_path_csv = "data.csv"
chunksize = 20000
chunks = []# 读取CSV文件的每个块
for chunk in pd.read_csv(file_path_csv, chunksize=chunksize):chunks.append(chunk)# 将每个块的数据框存储在列表中
dataframes = []
for i, chunk in enumerate(chunks):df_name = f"A{i+1}"df = pd.DataFrame(chunk)dataframes.append(df)print(f"创建的数据框 {df_name}:\n", df)

运行结果

3.数据框关联操作

请根据以下定义的两个字典 dict1 和 dict2，完成如下任务：

dict1={'code':['A01','A01','A01','A02','A02','A02','A03','A03'],'month':['01','02','03','01','02','03','01','02'],'price':[10,12,13,15,17,20,10,9]}

dict2={'code':['A01','A01','A01','A02','A02','A02'],'month'：['01','02','03','01','02','03'], 'vol'：[10000,10110,20000,10002,12000,21000]}

1）将两个字典转化为数据框；

相关代码

import pandas as pd
# 定义字典
dict1 = {'code': ['A01', 'A01', 'A01', 'A02', 'A02', 'A02', 'A03', 'A03'],'month': ['01', '02', '03', '01', '02', '03', '01', '02'],'price': [10, 12, 13, 15, 17, 20, 10, 9]
}
dict2 = {'code': ['A01', 'A01', 'A01', 'A02', 'A02', 'A02'],'month': ['01', '02', '03', '01', '02', '03'],'vol': [10000, 10110, 20000, 10002, 12000, 21000]
}
# 将字典转换为数据框
df1 = pd.DataFrame(dict1)
df2 = pd.DataFrame(dict2)
print(df1)
print(df2)

运行结果

2）对两个数据框完成内连接、左连接、右连接，并将结果输出；

相关代码

import pandas as pd
# 定义字典
dict1 = {'code': ['A01', 'A01', 'A01', 'A02', 'A02', 'A02', 'A03', 'A03'],'month': ['01', '02', '03', '01', '02', '03', '01', '02'],'price': [10, 12, 13, 15, 17, 20, 10, 9]
}
dict2 = {'code': ['A01', 'A01', 'A01', 'A02', 'A02', 'A02'],'month': ['01', '02', '03', '01', '02', '03'],'vol': [10000, 10110, 20000, 10002, 12000, 21000]
}
# 将字典转换为数据框
df1 = pd.DataFrame(dict1)
df2 = pd.DataFrame(dict2)
# 1）内连接
inner_join = pd.merge(df1, df2, on=['code', 'month'], how='inner')
print("内连接结果：\n", inner_join)
# 2）左连接
left_join = pd.merge(df1, df2, on=['code', 'month'], how='left')
print("\n左连接结果：\n", left_join)
# 3）右连接
right_join = pd.merge(df1, df2, on=['code', 'month'], how='right')
print("\n右连接结果：\n", right_join)

运行结果

4.数据框合并操作

请定义三个字典dict1、dict2和dict3，完成如下任务：

dict1={'a':[2,2,'kt',6],'b':[4,6,7,8],'c':[6,5,np.nan,6]}

dict2={'d':[8,9,10,11],'e':['p',16,10,8]}

dict3={'a':[1,2],'b':[2,3],'c':[3,4],'d':[4,5],'e':[5,6]}

1）将三个字典转化为数据框df1、df2、df3；

相关代码

import pandas as pd
import numpy as np# 定义字典并转化为数据框
dict1 = {'a': [2, 2, 'kt', 6], 'b': [4, 6, 7, 8], 'c': [6, 5, np.nan, 6]}
dict2 = {'d': [8, 9, 10, 11], 'e': ['p', 16, 10, 8]}
dict3 = {'a': [1, 2], 'b': [2, 3], 'c': [3, 4], 'd': [4, 5], 'e': [5, 6]}
df1 = pd.DataFrame(dict1)
df2 = pd.DataFrame(dict2)
df3 = pd.DataFrame(dict3)
# 1）将三个字典转化为数据框
print("df1:")
print(df1)
print("\ndf2:")
print(df2)
print("\ndf3:")
print(df3)

运行结果

2）df1和df2进行水平合并，合并后的数据框记为df4；

相关代码

# 2）df1和df2进行水平合并
df4 = pd.concat([df1, df2], axis=1)
print("\ndf1和df2水平合并结果df4：")
print(df4)

运行结果

3）df3和df4垂直合并，并修改合并后的index为按默认顺序排列。

相关代码

# 3）df3和df4垂直合并，并修改合并后的index为按默认顺序排列
df_final = pd.concat([df3, df4], axis=0).reset_index(drop=True)
print("\ndf3和df4垂直合并结果（重置索引后）：")
print(df_final)

运行结果

5.序列移动计算方法应用

定义列表L=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]，并转化为序列S，采用序列中的方法，实现周期为10的移动求和、求平均值、求最大值、求最小值的计算，并输出序列为10的移动计算的最小值的结果。

相关代码

import pandas as pd
L = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
S = pd.Series(L)
# 移动求和
moving_sum = S.rolling(window=10).sum()
# 求平均值
moving_mean = S.rolling(window=10).mean()
# 求最大值
moving_max = S.rolling(window=10).max()
# 求最小值
moving_min = S.rolling(window=10).min()
print("移动求和结果：", moving_sum)
print("平均值结果：", moving_mean)
print("最大值结果：", moving_max)
print("最小值结果：", moving_min)

运行结果

6.数据框切片（iloc、loc）方法

数据框中有两种方式可以实现切片，通过索引实现（iloc）和列标签实现（loc）。请读取地铁站点进出站客流数据表（Data.xlsx），并完成如下任务：

1）采用索引实现的方式，获取135站点10月1日-10月2日早上9-11点3个时刻的进站客流量数据；

相关代码

运行结果

2）采用列标签实现方式，获取135站点10月1日-10月2日早上9-11点3个时刻的进站客流量数据。

相关代码

运行结果

7.数据框排序

读取股票交易数据表（stkdata.xlsx），完成如下任务：

1）提取600000.SH代码交易数据，并按交易日期从小到大进行排序；

相关代码

运行结果

2）对整个数据表按代码、交易日期从小到大进行排序。

相关代码

运行结果

8.逻辑索引、切片方法，groupby 分组计算函数应用

请读取地铁站点进出站客流数据表(Data.xlsx)，完成以下任务：

1）取出第0列，通过去重的方式获得地铁站点编号列表,记为code.

相关代码

运行结果

2）采用数据框中的groupby分组计算函数，统计出每个地铁站点每天的进站人数和出站人数，计算结果采用一个数据框sat_num来表示，其中列标签依次为:站点编号、日期、进站人数和出站人数；

相关代码

运行结果

3）计算出每个站点国庆节期间（10.1~10.7）的进站人数和出站人数，计算结果用一个数据框sat_num2来表示，其中列标签依次为:A1_站点编号、A2_进站人数、A3_出站人数。

相关代码

运行结果

三、Matplotlib

Matplotlib 是一个用于 Python 语言的绘图库，主要用于创建高质量的数据可视化图形。它是开源的，并且非常流行，在数据分析、科学计算、工程绘图及教育领域有着广泛的应用。

Matplotlib 的定义要点：

绘图库：Matplotlib 提供了一整套绘制静态、动态和交互式图形的功能，尤其专注于二维数据可视化，同时也支持一些基本的三维图表。
功能全面：它能够绘制各种类型的图表，包括但不限于折线图（line plots）、散点图（scatter plots）、柱状图（bar charts）、饼图（pie charts）、直方图（histograms）、箱线图（box plots）、等高线图（contour plots）、热力图（heatmap）、3D表面图（3D surface plots）等。
高度定制化：Matplotlib 允许用户对图形的各种细节进行精细化控制，包括颜色、线型、标记样式、字体、布局、坐标轴、图例、注释、文本标注等。
兼容性好：可以与其他 Python 库如 NumPy、Pandas 等无缝配合，能够直接处理这些库产生的数据结构，简化数据可视化过程。
输出形式多样：创建的图表可以保存为多种格式，例如 PNG、JPEG、SVG、PDF 等，也可以显示在交互式环境中，如 Jupyter Notebook 或 GUI 应用程序内。

Matplotlib 的使用领域：

科学研究：科学家在发表论文时经常使用 Matplotlib 来展示实验结果和模拟数据，生成可供出版的质量极高的图形。
数据分析：数据分析人员利用 Matplotlib 来快速探索数据集，揭示数据之间的关系和趋势，辅助做出业务决策。
教育领域：在数学、物理、工程等相关课程的教学中，Matplotlib 被用来清晰地演示数学概念和实验结果。
商业报告：商业智能和市场研究团队会用 Matplotlib 来可视化业务指标、客户行为分析等，以直观的形式展现给管理层或客户。
工程绘图：工程师在处理仿真结果、测量数据或设备性能数据时，可以通过 Matplotlib 进行图形化展示和分析。

总之，Matplotlib 是一个通用性强、适应面广的数据可视化工具，对于任何需要用图形来表达数据含义、解释复杂现象或者交流研究成果的场景，都具有很高的实用价值。

各站点各时刻进出站客流数据.xlsx部分数据

站点编号 日期时刻 进站人数 出站人数
155 2015-10-01 7 294 1215
155 2015-10-01 8 1128 4067
155 2015-10-01 9 1441 3713
155 2015-10-01 10 2043 2976
155 2015-10-01 11 2678 3198
155 2015-10-01 12 2515 2804
155 2015-10-01 13 2313 2396
155 2015-10-01 14 1767 2680
155 2015-10-01 15 1873 2202

1.散点图绘制

读取“各站点各时刻进出站客流数据.xlsx”，绘制站点155各时刻进站客流散点图。

相关代码

import pandas as pd
import matplotlib.pyplot as plt# 读取数据
data = pd.read_excel("各站点各时刻进出站客流数据.xlsx")
plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置字体为SimHei
plt.rcParams['axes.unicode_minus'] = False  # 解决负号“-”显示异常
"""
（1）散点图绘制
读取“各站点各时刻进出站客流数据.xlsx”，绘制站点155各时刻进站客流散点图。
"""# 筛选出站点155的数据
site_155_data = data[data["站点编号"] == 155]
# 使用groupby按“时刻”聚合数据，并计算每个时刻的“进站人数”之和
aggregate_data = site_155_data.groupby("时刻")["进站人数"].sum().reset_index()
# 绘制散点图
plt.scatter(aggregate_data["时刻"], aggregate_data["进站人数"])
plt.xlabel("时刻")
plt.ylabel("进站总人数")  # 修改标签为进站总人数
plt.title("站点155各时刻进站客流散点图")  # 修改标题为进站总人数散点图
plt.show()

运行结果

2.线性图绘制

读取“各站点各时刻进出站客流数据.xlsx”，绘制站点157各时刻进站客流线形图。

相关代码

import pandas as pd
import matplotlib.pyplot as plt# 读取数据
data = pd.read_excel("各站点各时刻进出站客流数据.xlsx")
plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置字体为SimHei
plt.rcParams['axes.unicode_minus'] = False  # 解决负号“-”显示异常
sites = [157]
fig, ax = plt.subplots(figsize=(10, 8))for i, site in enumerate(sites):site_data = data[data["站点编号"] == site]total_counts = site_data.groupby("时刻")["进站人数"].sum()ax.plot(total_counts.index, total_counts.values)ax.set_title(f"站点{site}各时刻进站客流线性图")ax.set_xlabel("时刻")ax.set_ylabel("总进站人数")plt.tight_layout()
plt.show()

运行结果

3.柱状图绘制

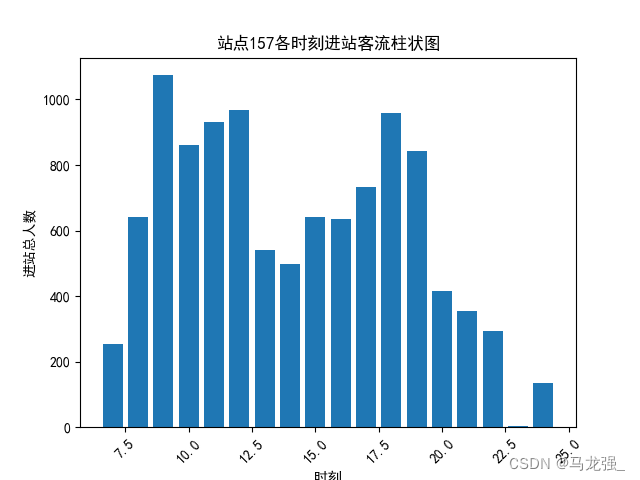
读取“各站点各时刻进出站客流数据.xlsx”，绘制站点157各时刻进站客流柱状图。

相关代码

import pandas as pd
import matplotlib.pyplot as plt# 读取数据
data = pd.read_excel("各站点各时刻进出站客流数据.xlsx")
plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置字体为SimHei
plt.rcParams['axes.unicode_minus'] = False  # 解决负号“-”显示异常
# 筛选出站点157的数据
site_157_data = data[data["站点编号"] == 157]# 使用groupby按“时刻”聚合数据，并计算每个时刻的“进站人数”之和
aggregate_data = site_157_data.groupby("时刻")["进站人数"].sum().reset_index()
# 绘制柱状图
plt.bar(aggregate_data["时刻"], aggregate_data["进站人数"])
plt.xlabel("时刻")
plt.ylabel("进站总人数")  # 修改标签为进站总人数
plt.title("站点157各时刻进站客流柱状图")  # 修改标题为进站总人数柱状图
plt.xticks(rotation=45)  # 如果时刻标签较长，可以旋转x轴标签以便阅读
plt.show()

运行结果

4.直方图绘制

读取“各站点各时刻进出站客流数据.xlsx”，绘制站点157各时刻进站客流直方图。

相关代码

import pandas as pd
import matplotlib.pyplot as plt# 读取数据
data = pd.read_excel("各站点各时刻进出站客流数据.xlsx")
plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置字体为SimHei
plt.rcParams['axes.unicode_minus'] = False  # 解决负号“-”显示异常
# 筛选出站点157的数据
site_157_data = data[data["站点编号"] == 157]
# 使用groupby按“时刻”聚合数据，并计算每个时刻的“进站人数”之和
aggregate_data = site_157_data.groupby("时刻")["进站人数"].sum().reset_index()
# 绘制直方图
plt.hist(aggregate_data["进站人数"], bins=10)  # 设置bins参数来控制直方图的柱子数量
plt.xlabel("进站总人数")
plt.ylabel("频数")
plt.title("站点157各时刻进站客流直方图")
plt.show()

运行结果

5.饼图绘制

读取 “各站点各时刻进出站客流数据.xlsx”，绘制站点157各时刻进站客流饼图。

相关代码

import pandas as pd
import matplotlib.pyplot as plt# 读取数据
data = pd.read_excel("各站点各时刻进出站客流数据.xlsx")
plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置字体为SimHei
plt.rcParams['axes.unicode_minus'] = False  # 解决负号“-”显示异常
# 筛选出站点157的数据
site_157_data = data[data["站点编号"] == 157]
# 饼图不适合展示时间序列数据，但可以展示每个时刻进站人数占全天进站人数的比例
pie_data = site_157_data.groupby("时刻")["进站人数"].sum()
plt.pie(pie_data, labels=pie_data.index, autopct="%1.1f%%")
plt.title("站点157各时刻进站客流饼图")
plt.show()

运行结果

6.箱线图绘制

读取“各站点各时刻进出站客流数据.xlsx”，绘制各站点在9时刻进站客流的箱线图。

相关代码

import pandas as pd
import matplotlib.pyplot as plt# 读取数据
data = pd.read_excel("各站点各时刻进出站客流数据.xlsx")
plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置字体为SimHei
plt.rcParams['axes.unicode_minus'] = False  # 解决负号“-”显示异常
# 筛选9时刻的进站客流数据
nine_am_data = data[(data["时刻"] == 9)][["站点编号", "进站人数"]]# 按站点编号分组并计算进站人数的列表
station_flows = nine_am_data.groupby("站点编号")["进站人数"].apply(list).to_dict()# 绘制箱线图
plt.boxplot(station_flows.values(), labels=station_flows.keys())
plt.xlabel("站点编号")
plt.ylabel("进站人数")
plt.title("各站点在9时刻进站客流的箱线图")
plt.show()

运行结果

7.子图绘制

读取“各站点各时刻进出站客流数据.xlsx”，将155、157、151、123四个站点在各时刻的进站客流，用一个2*2的子图，绘制其线性图。

相关代码

import pandas as pd
import matplotlib.pyplot as plt# 读取Excel文件
df = pd.read_excel('各站点各时刻进出站客流数据.xlsx')
plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置字体为SimHei
plt.rcParams['axes.unicode_minus'] = False  # 解决负号“-”显示异常
# 定义需要绘图的站点编号
stations = [155, 157, 151, 123]
# 初始化子图位置
subplot_positions = [(1, 1), (1, 2), (2, 1), (2, 2)]
# 初始化一个空的字典来存储每个站点的聚合数据
station_data = {}
# 遍历站点列表，对每个站点进行聚合
for station in stations:# 筛选出特定站点的数据station_df = df[df['站点编号'] == station]# 以时刻为索引，对进站人数进行求和aggregated_data = station_df.groupby('时刻')['进站人数'].sum().reset_index()# 将聚合后的数据存储在字典中station_data[station] = aggregated_data
# 绘制2x2子图
fig, axs = plt.subplots(2, 2, figsize=(12, 8))
# 遍历站点和子图位置
for i, (station, data) in enumerate(station_data.items()):# 确定子图的位置row, col = subplot_positions[i]ax = axs[row - 1, col - 1]# 绘制线性图ax.plot(data['时刻'], data['进站人数'], marker='o', label=f'站点{station}')ax.set_xlabel('时刻')ax.set_ylabel('总进站人数')ax.set_title(f'站点{station}各时刻总进站客流线形图')ax.legend()
# 调整子图之间的间距
plt.tight_layout()
# 显示图形
plt.show()

运行结果

四、数据探索

波士顿房价数据集：卡内基梅隆大学收集，StatLib库，1978年，涵盖了麻省波士顿的506个不同郊区的房屋数据。

一共含有506条数据。每条数据14个字段，包含13个属性，和一个房价的平均值。

数据读取方法：

1.请绘制散点图探索波士顿房价数据集中犯罪率（CRIM）和房价中位数（MEDV）之间的相关性。

2.请使用波士顿房价数据集中房价中位数（MEDV）来绘制箱线图。

3.请使用暗点图矩阵探索波士顿房价数据集。

4.请分别使用皮尔逊（pearson）、斯皮尔曼（spearman）、肯德尔（kendall）相关系数对犯罪率（CRIM）和房价中位数（MEDV）之间的相关性进行度量。

5.请绘制波士顿房价数据集中各变量之间相关系数的热力图。

需提前安装seaborn库：pip install seaborn

热力图绘制方法：

五、数据预处理

1.读取“银行贷款审批数据.xlsx”表，自变量为x1-x14，决策变量为y（1-同意贷款，0-不同意贷款），自变量中有连续变量（x2,x3,x5,x6,x7,x10,x13,x14）和离散变量（x1,x4,x8,x9,x11,x12），请对连续变量中的缺失值用均值策略填充，对离散变量中的缺失值用最频繁值策略填充。

2.请使用StandardScaler对波士顿房价数据集进行零-均值规范化。

3.在上一问规范化后的数据基础上使用PCA对数据进行降维处理（降维后的特征数量为2）。

站点编号	日期	时刻	进站人数	出站人数
155	2015-10-01	7	294	1215
155	2015-10-01	8	1128	4067
155	2015-10-01	9	1441	3713
155	2015-10-01	10	2043	2976
155	2015-10-01	11	2678	3198
155	2015-10-01	12	2515	2804
155	2015-10-01	13	2313	2396
155	2015-10-01	14	1767	2680
155	2015-10-01	15	1873	2202