ROC曲线（接收者操作特性曲线）和AUC（曲线下面积）是在不同阈值设置下，用于分类问题的性能度量工具。下面是它们所代表的含义以及使用方法：

ROC曲线

• 代表含义：ROC曲线是一个图形化的表示，说明了一个二分类器系统的诊断能力，随着其区分阈值的变化。它是通过在不同的阈值设置下，绘制真正例率（TPR，也称为召回率或灵敏度）与假正例率（FPR，或1 - 特异性）来创建的。
• 如何解读：曲线从（0,0）开始，到（1,1）结束。一个做出随机猜测的模型将会产生一条从图表左下角到右上角的对角线（无区分能力线）。曲线越远离这条对角线，模型的性能越好。

AUC - ROC曲线下面积

• 代表含义：AUC衡量的是整个ROC曲线下（从（0,0）到（1,1））的二维区域面积。它提供了一个在所有分类阈值上的综合性能度量。一个预测完全错误的模型有一个0.0的AUC；一个预测完全正确的模型的AUC为1.0。
• 如何解读：AUC可以被解释为模型对一个随机正例排名高于一个随机负例的概率。0.5的AUC表明没有区分能力（相当于随机猜测），接近1的AUC表示模型很好地将正例排名高于负例。

AUC 解释为排名概率：

• 把AUC想象成一个游戏，我们随机地从数据集中选取一个正例和一个负例。
• 然后我们让模型对这两个实例进行评分，预测它们是正例的概率。
• 如果模型通常能给正例更高的分数，这就意味着模型能很好地区分正例和负例。
• AUC值是模型在这个游戏中赢得每次比赛（即正例得分高于负例）的概率。

注：在二分类问题中，数据集被分成两类，通常一类是我们关注的目标，另一类则不是。这两类分别被称为“正例”和“负例”：

• 正例（Positive Case）：通常指的是我们试图检测或预测的类别。例如，在疾病诊断中，正例可能指的是患有某种疾病的病例；在垃圾邮件检测中，正例可能指的是垃圾邮件。

• 负例（Negative Case）：与正例相对，负例通常指的是除了正例之外的其它类别。在前面疾病诊断的例子中，负例可能指的是没有患病的健康病例；在垃圾邮件检测的例子中，负例可能指的是正常邮件。

在不同的应用场景中，哪些是正例哪些是负例，取决于问题的具体定义和研究的目的。正例和负例的概念有助于在建立模型时提供清晰的指导，以及在评估模型性能时，特别是计算诸如准确率、召回率、精确率这样的指标时，能够有明确的评判标准。

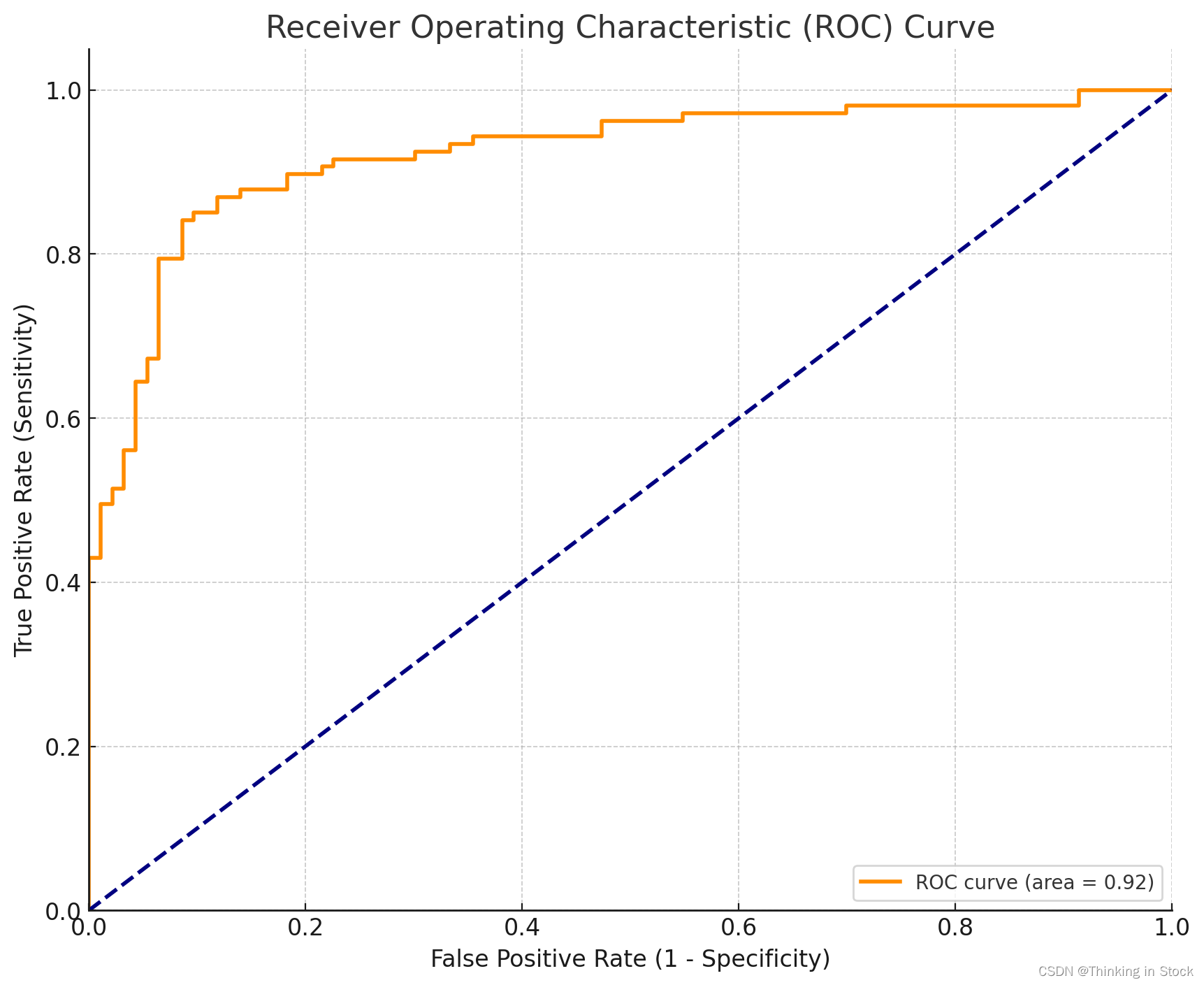
ROC曲线上的要点：

• x轴代表假正例率（FPR），y轴代表真正例率（TPR）。
• 蓝色虚线代表完全随机分类器的ROC曲线（AUC为0.5）；它是衡量分类器的基准线。
• 橙色曲线代表逻辑回归分类器的ROC曲线。它展示了灵敏度和特异性之间的权衡（即真正例和假正例之间的权衡）。
• AUC（曲线下面积）值为0.92，接近于1，表示模型具有良好的可分性。AUC越接近1，模型在将0预测为0和1预测为1方面就越好。
• 完美的分类器将有一条线从左下角（0假正例）到左上角（100%真正例），然后到右上角（100%真正例在100%假正例时）。

ROC-AUC得分是一个单一的标量值，总结了分类器在所有阈值下的性能，这使得它在需要评估和比较分类器时非常方便。

从图中我们可以得出结论，分类器的表现明显优于随机猜测，因为曲线更接近左上角。这使得它成为一个可能的好模型，用于它被设计的预测任务。

图表上的阈值：

• 在图表上，每个点对应一个特定的阈值设置。当你沿着ROC曲线移动时，这个阈值是变化的，每个点代表了在特定阈值下模型的TPR和FPR。
• 例如，如果一个点位于曲线的右上角，它可能对应一个较低的阈值，此时有高真正例率和高假正例率。
• 如果一个点位于曲线的左上角，它可能对应一个较高的阈值，此时有高真正例率和低假正例率。

根据具体情况，我们可能会调整阈值。例如，如果我们非常重视避免误判负例为正例（即希望降低FPR），我们可能会选择一个更高的阈值，即使这会降低TPR。相反，如果我们更希望不漏掉任何正例（即希望提高TPR），我们可能会选择一个更低的阈值，即使这意味着更高的FPR。

为什么ROC-AUC很有价值：

• 阈值不变性：ROC-AUC之所以有价值，是因为它评估了模型在所有分类阈值下的性能，提供了一个不依赖于特定截断点的质量度量。
• 分类不平衡问题：它在类别不平衡的情况下特别有用，因为它同时考虑了假正例率和真正例率。在类别不平衡的数据中，诸如准确率这样的指标可能会产生误导，但AUC提供了一个更细致、更全面的度量。
• 模型比较：AUC指标允许我们比较不同模型，并决定哪个模型在区分类别方面可能更好。

在实践中，为了计算ROC-AUC，你通常会使用一个工具或库函数，该函数接收真实结果和正类的预测概率，计算不同阈值下的TPR和FPR，然后对曲线进行积分以找到AUC。在Python中，这个功能由像`scikit-learn`这样的库提供。

from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression# Create a synthetic binary classification dataset
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)# Split the data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# Train a logistic regression classifier
clf = LogisticRegression(random_state=42)
clf.fit(X_train, y_train)# Predict probabilities for the test set
y_scores = clf.predict_proba(X_test)[:, 1]# Compute ROC curve and ROC area
fpr, tpr, _ = roc_curve(y_test, y_scores)
roc_auc = auc(fpr, tpr)# Plotting the ROC curve
plt.figure(figsize=(10, 8))
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate (1 - Specificity)')
plt.ylabel('True Positive Rate (Sensitivity)')
plt.title('Receiver Operating Characteristic (ROC) Curve')
plt.legend(loc="lower right")
plt.show()