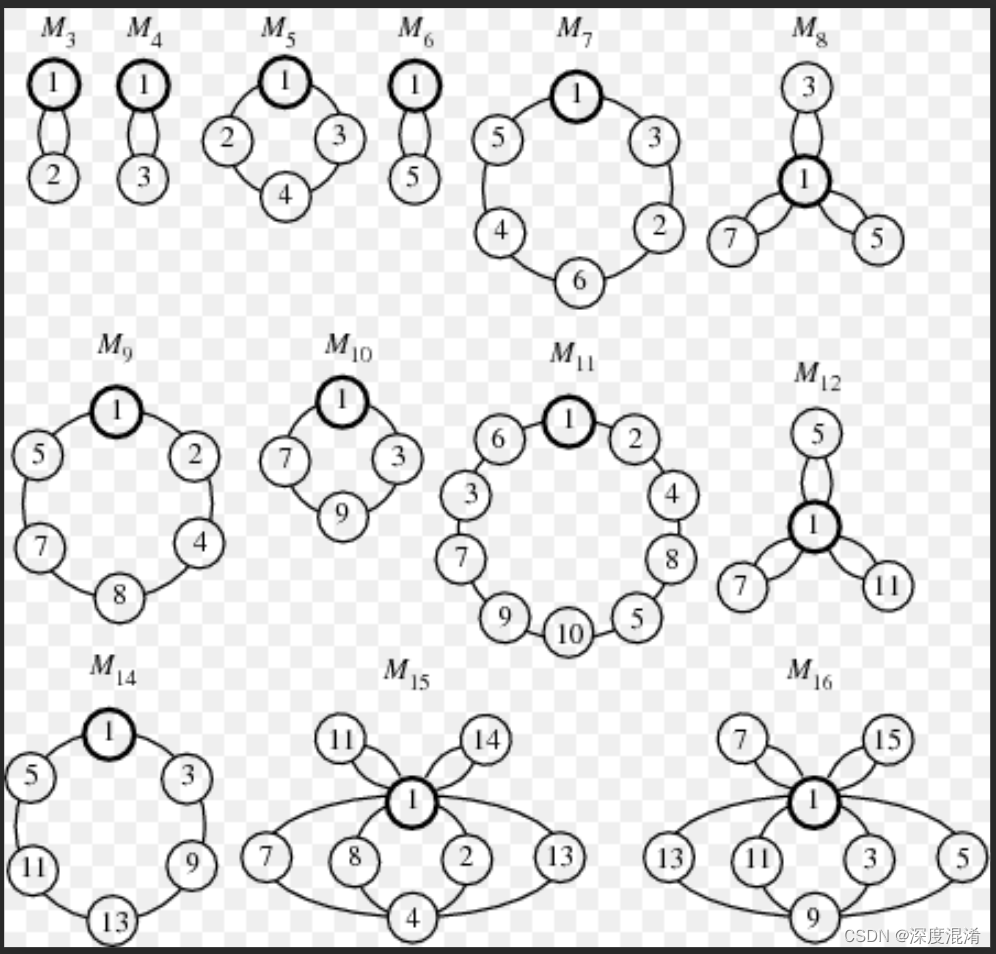
1 无向连通图中长度为n环

给定一个无向连通图和一个数n，计算图中长度为n的环的总数。长度为n的循环仅表示该循环包含n个顶点和n条边。我们必须统计存在的所有这样的环。

为了解决这个问题，可以有效地使用DFS（深度优先搜索）。使用DFS，我们可以找到特定源（或起点）的长度（n-1）的所有可能路径。然后我们检查该路径是否以其开始的顶点结束，如果是，则将其计为长度为n的循环。注意，我们查找长度为n-1的路径，因为第n条边将是循环的闭合边。

可以仅使用V–（n–1）个顶点（其中V是顶点总数）搜索长度（n-1）的每个可能路径。

对于上面的示例，可以仅使用5-（4-1）=2个顶点搜索长度为4的所有循环。这背后的原因很简单，因为我们使用这2个顶点（包括其余3个顶点）搜索所有可能的长度（n-1）=3的路径。因此，这两个顶点也覆盖了其余3个顶点的循环，并且仅使用3个顶点，我们无论如何都不能形成长度为4的循环。

还有一点需要注意的是，每个顶点为其形成的每个循环找到2个重复的循环。对于上面的示例，第0个顶点找到两个重复的循环，即0->3->2->1->0和0->1->2->3->0。因此，总计数必须除以2，因为每个周期计数两次。