文章目录
- 三角函数
- 定义式
- 诱导公式
- 平方关系
- 两角和与差的三角函数
- 积化和差公式
- 和差化积公式
- 倍角公式
- 半角公式
- 万能公式
- 其他公式
- 反三角函数恒等式
- 三角函数
- 定义式
三角函数
定义式
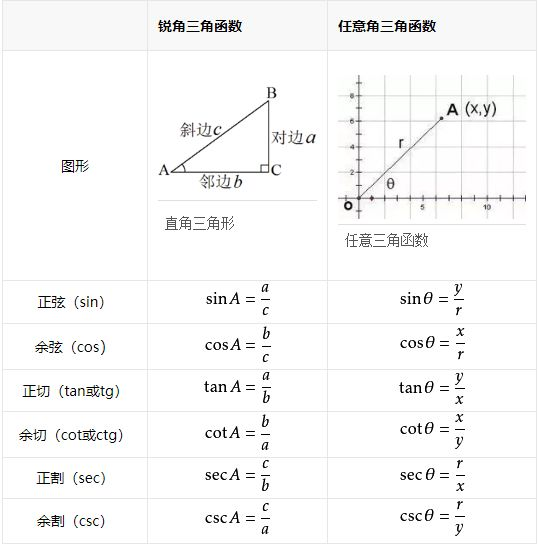
余切: c o t A = 1 t a n A \text { 余切:} \ cotA = \frac{1}{tanA} 余切: cotA=tanA1
正切: s e c A = 1 c o s A \text { 正切:} \ secA = \frac{1}{cosA} 正切: secA=cosA1
余割: c s c A = 1 s i n A \text { 余割:} \ cscA = \frac{1}{sinA} 余割: cscA=sinA1
反正切: a r c t a n ( t a n X ) = t a n ( a r c t a n X ) = X \text { 反正切:} \ arctan(tanX) = tan(arctanX) = X 反正切: arctan(tanX)=tan(arctanX)=X
诱导公式
- sin ( − α ) = − sin α
- cos ( − α ) = cos α
- sin ( π 2 − α ) = cos α
- cos ( π 2 − α ) = sin α
- sin ( π 2 + α ) = cos α
- cos ( π 2 + α ) = − sin α
- sin ( π − α ) = sin α
- cos ( π − α ) = − cos α
- sin ( π + α ) = − sin α
- cos ( π + α ) = − cos α
平方关系
1 + t a n 2 α = s e c 2 α 1 + tan^2α = sec^2α 1+tan2α=sec2α
1 + c o t 2 α = c s c 2 α 1 + cot^2α = csc^2α 1+cot2α=csc2α
s i n 2 α + c o s 2 α = 1 sin^2α + cos^2α = 1 sin2α+cos2α=1
两角和与差的三角函数
s i n ( α + β ) = s i n α c o s β + c o s α s i n β sin ( α + β ) = sin α cos β + cos α sin β sin(α+β)=sinαcosβ+cosαsinβ
c o s ( α + β ) = c o s α c o s β − s i n α s i n β cos ( α + β ) = cos α cos β − sin α sin β cos(α+β)=cosαcosβ−sinαsinβ
s i n ( α − β ) = s i n α c o s β − c o s α s i n β sin ( α − β ) = sin α cos β − cos α sin β sin(α−β)=sinαcosβ−cosαsinβ
c o s ( α − β ) = c o s α c o s β + s i n α s i n β cos ( α − β ) = cos α cos β + sin α sin β cos(α−β)=cosαcosβ+sinαsinβ
t a n ( α + β ) = t a n α + t a n β 1 − t a n α t a n β tan ( α + β ) = \frac{ tan α + tan β}{1 - tan α tan β} tan(α+β)=1−tanαtanβtanα+tanβ
t a n ( α − β ) = t a n α − t a n β 1 + t a n α t a n β tan ( α − β ) = \frac{ tan α - tan β}{1 + tan α tan β} tan(α−β)=1+tanαtanβtanα−tanβ
积化和差公式
c o s α c o s β = 1 2 [ c o s ( α + β ) + c o s ( α − β ) ] cos α cos β = \frac{1}{2} [ cos ( α + β ) + c o s ( α − β ) ] cosαcosβ=21[cos(α+β)+cos(α−β)]
c o s α s i n β = 1 2 [ s i n ( α + β ) − s i n ( α − β ) ] cos α sin β = \frac{1}{2} [ sin ( α + β ) - sin ( α − β ) ] cosαsinβ=21[sin(α+β)−sin(α−β)]
s i n α c o s β = 1 2 [ s i n ( α + β ) + s i n ( α − β ) ] sin α cos β = \frac{1}{2} [ sin ( α + β ) + sin ( α − β ) ] sinαcosβ=21[sin(α+β)+sin(α−β)]
s i n α s i n β = − 1 2 [ c o s ( α + β ) + c o s ( α − β ) ] sin α sin β = -\frac{1}{2} [ cos ( α + β ) + c o s ( α − β ) ] sinαsinβ=−21[cos(α+β)+cos(α−β)]
和差化积公式
s i n α + s i n β = 2 s i n α + β 2 c o s α − β 2 sin α + sin β = 2 sin \frac{α + β}{2} cos \frac{α - β}{2} sinα+sinβ=2sin2α+βcos2α−β
s i n α − s i n β = 2 c o s α + β 2 s i n α − β 2 sin α - sin β = 2 cos \frac{α + β}{2} sin \frac{α - β}{2} sinα−sinβ=2cos2α+βsin2α−β
c o s α + c o s β = 2 c o s α + β 2 c o s α − β 2 cos α + cos β = 2 cos \frac{α + β}{2} cos \frac{α - β}{2} cosα+cosβ=2cos2α+βcos2α−β
c o s α − c o s β = − 2 s i n α + β 2 s i n α − β 2 cos α - cos β = -2 sin \frac{α + β}{2} sin \frac{α - β}{2} cosα−cosβ=−2sin2α+βsin2α−β
倍角公式
s i n 2 α = 2 s i n α c o s α sin 2 α = 2 sin α cos α sin2α=2sinαcosα
c o s 2 α = c o s 2 α − s i n 2 α = 1 − 2 s i n 2 α = 2 c o s 2 α − 1 cos 2 α = cos ^2 α − sin ^2 α = 1 − 2 sin ^2 α = 2 cos ^2 α − 1 cos2α=cos2α−sin2α=1−2sin2α=2cos2α−1
s i n 3 α = − 4 s i n 3 α + 3 s i n α sin 3 α = − 4 sin ^3 α + 3 sin α sin3α=−4sin3α+3sinα
c o s 3 α = 4 c o s 3 α − 3 c o s α cos 3 α = 4 cos ^3 α − 3 cos α cos3α=4cos3α−3cosα
s i n 2 α = 1 − c o s 2 α 2 sin ^2 α = \frac{1 − cos 2 α}{2} sin2α=21−cos2α
c o s 2 α = 1 + c o s 2 α 2 cos ^2 α = \frac{1 + cos 2 α}{2} cos2α=21+cos2α
t a n 2 α = 2 t a n α 1 − t a n 2 α tan 2 α = \frac{2 tan α}{1 − tan ^2 α } tan2α=1−tan2α2tanα
c o t 2 α = c o t 2 α − 1 2 c o t α cot 2 α = \frac{cot ^2 α − 1}{2 cot α} cot2α=2cotαcot2α−1
半角公式
s i n 2 α 2 = 1 − c o s α 2 sin ^2 \frac{α}{2} = \frac{1 − cos α}{2} sin22α=21−cosα
c o s 2 α 2 = 1 + c o s α 2 cos ^2 \frac{α}{2} = \frac{1 + cos α}{2} cos22α=21+cosα
s i n α 2 = ± 1 − c o s α 2 sin \frac{α}{2} = ±\sqrt{\frac{1 - cos α}{2}} sin2α=±21−cosα
c o s α 2 = ± 1 + c o s α 2 cos \frac{α}{2} = ±\sqrt{\frac{1 + cos α}{2}} cos2α=±21+cosα
t a n α 2 = 1 − c o s α s i n α = s i n α 1 + c o s α = ± 1 − c o s α 1 + c o s α tan \frac{α}{2} = \frac{1 - cos α}{sin α} = \frac{sin α}{1 + cos α } = ±\sqrt{\frac{1 - cos α}{1 + cos α}} tan2α=sinα1−cosα=1+cosαsinα=±1+cosα1−cosα
c o t α 2 = s i n α 1 − c o s α = 1 + c o s α s i n α = ± 1 + c o s α 1 − c o s α cot \frac{α}{2} = \frac{sin α}{1 - cos α} = \frac{1 + cos α }{sin α } = ±\sqrt{\frac{1 + cos α}{1 - cos α}} cot2α=1−cosαsinα=sinα1+cosα=±1−cosα1+cosα
万能公式
s i n α = 2 t a n α 2 1 + t a n 2 α 2 sin α = \frac{2tan \frac{α}{2}}{1 + tan ^2 \frac{α}{2}} sinα=1+tan22α2tan2α
c o s α = 1 − t a n 2 α 2 1 + t a n 2 α 2 cos α = \frac{1 - tan ^2 \frac{α}{2}}{1 + tan ^2 \frac{α}{2}} cosα=1+tan22α1−tan22α
其他公式
1 + s i n α = ( s i n α 2 + c o s α 2 ) 2 1 + sin α = ( sin \frac{α}{2} + cos \frac{α}{2}) ^2 1+sinα=(sin2α+cos2α)2
1 − s i n α = ( s i n α 2 − c o s α 2 ) 2 1 - sin α = ( sin \frac{α}{2} - cos \frac{α}{2}) ^2 1−sinα=(sin2α−cos2α)2
反三角函数恒等式
a r c s i n x + a r c c o s x = π 2 arcsin x + arccos x = \frac{π}{2} arcsinx+arccosx=2π
a r c t a n x + a r c c o t x = π 2 arctan x + arccot x = \frac{π}{2} arctanx+arccotx=2π
s i n ( a r c c o s x ) = 1 − x 2 sin ( arccos x ) = \sqrt{1 − x ^2} sin(arccosx)=1−x2
c o s ( a r c s i n x ) = 1 − x 2 cos ( arcsin x ) = \sqrt{1 − x ^2} cos(arcsinx)=1−x2
s i n ( a r c s i n x ) = x sin ( arcsin x ) = x sin(arcsinx)=x
a r c s i n ( s i n x ) = x arcsin ( sin x ) = x arcsin(sinx)=x
c o s ( a r c c o s x ) = x cos ( arccos x ) = x cos(arccosx)=x
a r c c o s ( c o s x ) = x arccos ( cos x ) = x arccos(cosx)=x
a r c c o s ( − x ) = π − a r c c o s x arccos ( − x ) = π − arccos x arccos(−x)=π−arccosx