一、要求

1.计算sigmoid函数的梯度；

2．随机初始化网络权重；

3.编写网络的代价函数。

二、算法介绍

神经网络结构：

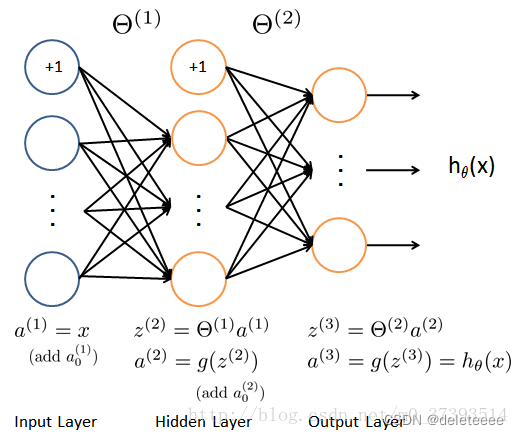
不正则化的神经网络的代价函数：

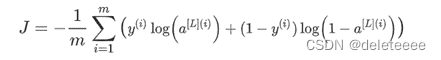
正则化：

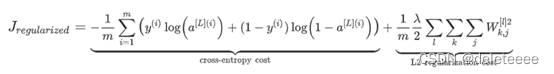
S型函数求导：

反向传播算法：

step1：初始化 ，然后使用前向传播算法计算

step2：计算第三层的误差 ；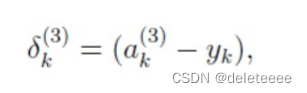

step3：对于第二层  ；

step4：使用公式 累积这个例子的所有的梯度！注意你需要跳过或者移除 ， ；

step5：通过将之前累积的梯度除以m得到没有正则化的神经网络代价函数的梯度；

三、过程记录

1.可视化数据集

导入数据集后，通过displayData函数将数据集显示出来，由于数据集数据较大，随机选取100个数据点进行显示，结果如下：

图1 显示数据集

2.模型表示

构造的神经网络包含输入层，隐含层，输出层，由于图像大小为20×20，所以设定输入层大小为400，设定隐藏层大小为25，标签一共10个。

3.前馈与成本函数

将标签重新编码为只包含0和1的向量，在标签向量y中找到标签号对应的位置，在将新的向量中放入处理后的值，处理的要求是将一维标签号i改为十维向量，其中第i个位置为1其余为0，如3处理后为[0 0 1 0 0 0 0 0 0 0]

接下来再正则化成本函数

导入θ1和θ2的参数集，θ1不参与正则化，对相应参数进行处理然后通过公式计算得出

当lambda设定为0时，结果如下：

图2 lambda=0代价值

Lambda为1时：

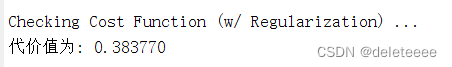
图3 lambda=1代价值

4.反向传播

该部分需要用到sigmoid函数，在之前实验已经成功编写，通过如下语句可以在sigmoidGradient中实现对sigmoid函数梯度的计算：

给出示例进行测试：

结果如下：

图4 验证sigmoid梯度函数

接下来初始化θ的权重，通过随机选取[-0.12 0.12]范围内的值以确保参数保持较小使学习有效，初始化函数randInitializeWeights中代码如下：

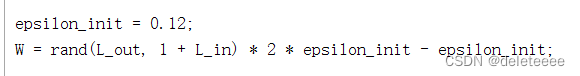
完成后进行调用：

然后完成正则化反向传播算法，通过循环对不同示例进行处理，每一次需要完成四个步骤：将输入层的值设置为第t个训练示例、对于输出层每个单元k进行处理、对于隐藏层进行设置、累计梯度。最后将累计梯度除以示例的个数m得到神经网络的代价函数梯度。

完成上述之后通过checkNNGradients函数检查梯度，该函数将创造一个小的神经网络和数据集进行测试，结果如下：

图5 梯度检查结果

从图中可以看出左右两边梯度值非常相似，最终计算出来的相对差异也小于1e-9，说明梯度计算正确。

5.使用函数fmincg来优化学习参数

设置最大迭代次数为50次，lambda=1，通过fmincg函数训练迭代寻找得到最佳的参数θ

训练部分过程如下：

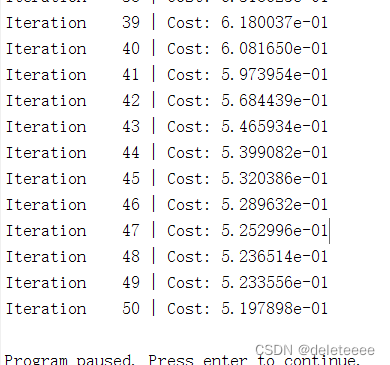
图6 训练过程

可以看出代价值在不断减小，寻找最佳的状态

6.预测并计算准确率

通过predict函数实现预测的功能，其中代码如下：

将θ1和θ2以及预测样本传入函数中得到p即为预测值，再与训练集真实值进行比较得到准确率如下：

图7 训练集准确率

7.可视化隐藏层

为了理解神经网络在学习什么，通过displayData函数将其可视化：

结果如下：

图8 可视化隐藏层

图中一共有25个单元，每个单元对应网络中的一个隐藏单元。

8.修改参数进一步实验

为了更深入地了解神经网络的性能如何随正则化参数λ和训练步骤数而变化的，对程序中的参数进行修改并观察结果：

图9 λ=0.5

图10 λ=0.01

图11 λ=10

图12 λ=100

图13 迭代次数为100

图14 迭代次数为500

四、结果分析

    通过上述实验分析可知，实验中构造的反向传播神经网络能够较为准确的识别出数据集中的手写数字。在实验过程中由成本函数和梯度等一些计算中以及优化参数的过程中，正则化参数和迭代次数的设定对实验的结果有一定的影响，通过进一步探究发现，正则化参数值减小，训练集精度会有一定的增大如图9与图10，而若正则化参数增大则训练集精度可能会减小如图11和图12所示。可知，正则化可以防止过拟合，正则化参数太小容易产生过拟合，太大容易产生欠拟合，在无法增加样本数量或增加样本数量的成本过高时，正则化是一种行之有效的方法。又由于优化参数的过程是一个迭代寻优的过程，成本函数的值会不断降低，迭代次数增大后训练集精度有显著上升，如图13和图14所示。