前言

        在当今科技高速发展的时代，数学建模成为了解析复杂世界的关键工具，而MATLAB作为一种专业的科学计算软件，为我们提供了强大的数学建模平台。MATLAB不仅仅是Matrix Laboratory的简称，更是一个集数值分析、矩阵计算、算法开发和可视化于一体的软件环境。

数学建模的核心基础知识：MATLAB入门

        数学建模的基础是对模型中使用的数学和物理概念的深入了解。在MATLAB中建模，首先要熟悉其环境。MATLAB的界面包括命令窗口、工作区、路径管理器和文件编辑器等几个主要部分，每一部分都为模型的开发和测试提供了便利。

数据和函数的基本操作

        在MATLAB中，数据管理和函数的应用是编程的核心内容。为了充分利用MATLAB的强大功能进行数据分析和数学建模，必须掌握对数组和矩阵的基本操作以及编写和调用函数的方法。

数据操作

数组和矩阵的创建与操作：

        矩阵是MATLAB中最基本的数据结构。操作矩阵的基础功能非常强大，可以涵盖从基础算术到复杂的数学运算。

示例代码：创建和转置矩阵

% 创建一个3x3的矩阵
A = [1, 2, 3; 4, 5, 6; 7, 8, 9];% 转置矩阵
A_transposed = A';

向量的创建与索引：

        向量可以是行向量或列向量，并且在数学建模中经常用作数据集合或参数列表。

示例代码：创建等差向量并访问元素

% 创建一个包含从1到10的等差序列的向量，步长为0.1
v = 1:0.1:10;% 访问向量的第五个元素
fifth_element = v(5);

函数操作

函数定义与调用：

        函数允许我们定义可重复使用的代码块，这在执行重复或标准计算时非常方便。

示例代码：定义一个计算圆的面积的函数

function area = calculateCircleArea(radius)% 计算圆的面积area = pi * radius^2;
end% 调用函数计算半径为5的圆的面积
circleArea = calculateCircleArea(5);

常用内置函数使用示例

        MATLAB的一个重要特性是它提供的大量内置函数，能够覆盖不同领域的需求，从基本的数学运算到复杂的数据分析和工程计算。

数学函数

平方根、和、平均值计算：

        这些常用的数学函数可以帮助我们快速对数据进行基本分析。

示例代码：使用内置函数处理向量

% 计算数字16的平方根
sqrt_result = sqrt(16);% 计算向量元素的和
vector_sum = sum([1, 2, 3, 4]);% 计算向量元素的平均值
vector_mean = mean([1, 2, 3, 4]);

数据分析函数

最大值、最小值和排序：

        处理矩阵和向量时，常常需要找到最大值、最小值，或对数据进行排序。

示例代码：寻找向量的最大值和排序

% 创建向量
data_vector = [10, 3, 7, 5, 9, 1];% 找到向量中的最大值
[max_value, max_index] = max(data_vector);% 对向量进行升序排序
sorted_vector = sort(data_vector);

数学建模的方法论：如何建模？

问题定义

        数学建模启动于一个问题或研究课题。在科研中，明确你的目标和所需解答的问题是初步阶段。接下来，将实际问题抽象成数学问题，确定关键参数和边界条件。

模型的假设

        您需要基于问题制定相应的假设来简化现实情况。例如，一个行星的运动模型通常会忽略非主要天体的影响，或者假设轨道为圆形而非椭圆。

数学工具和技巧的选择

        依据问题的类型和建立的假设，决定使用代数、微积分、统计、几何或其他数学工具。例如，在动力系统分析中，微分方程是描述系统行为的主要工具。

MATLAB中的实例展示

        我们通过一个太阳系简化模型来展示这个过程，当中，地球绕太阳公转的运动通过经典的二体问题来近似模拟。

        下面的代码展示了如何在MATLAB中创建一个简化版的太阳系模型，其中只考虑太阳和地球。这个模型使用二体近似，在这个假设下，太阳可以被视为系统的中心，而地球绕它的运动轨迹可以通过牛顿的万有引力定律和运动方程来计算。

        我们定义了地球与太阳之间的平均距离、地球的初始位置和速度向量，然后使用ode45这一MATLAB内置的常微分方程求解器来计算地球在一定时间跨度内的运动。

function solar_system_model% 定义了常数和初始条件G = 6.67430e-11; % 万有引力常数，m^3/kg/s^2M_sun = 1.989e30; % 太阳的质量，kgM_earth = 5.972e24; % 地球的质量，kgR = 1.496e11; % 地球和太阳之间平均距离，m% 地球绕太阳公转的角速度（简化为圆形轨道）omega = sqrt(G * M_sun / R^3);% 时间跨度：一年tspan = linspace(0, 2*pi/omega, 1000); % 分为1000个时间点% 初始位置和速度 [x0, y0, vx0, vy0]% 地球在x轴上，初始速度方向为y轴Y0 = [R, 0, 0, R * omega];% 使用ode45求解[t, Y] = ode45(@(t, y) two_body_equation(t, y, G, M_sun), tspan, Y0);% 画出轨道figure;plot(Y(:,1), Y(:,2));xlabel('x (m)');ylabel('y (m)');title('Earth orbit around the Sun using Two-Body Problem Simplification');axis equal;grid on;hold on;% 标记太阳的位置plot(0, 0, 'ro', 'MarkerSize', 15, 'MarkerFaceColor', 'r');
end% 本地函数 - 两体问题的微分方程
function dYdt = two_body_equation(t, Y, G, M_sun)% 提取位置和速度x = Y(1);y = Y(2);vx = Y(3);vy = Y(4);% 计算到太阳的距离r = sqrt(x^2 + y^2);% 根据万有引力定律计算加速度ax = -G * M_sun * x / r^3;ay = -G * M_sun * y / r^3;% 返回位置的导数(速度)和速度的导数(加速度)dYdt = [vx; vy; ax; ay];
end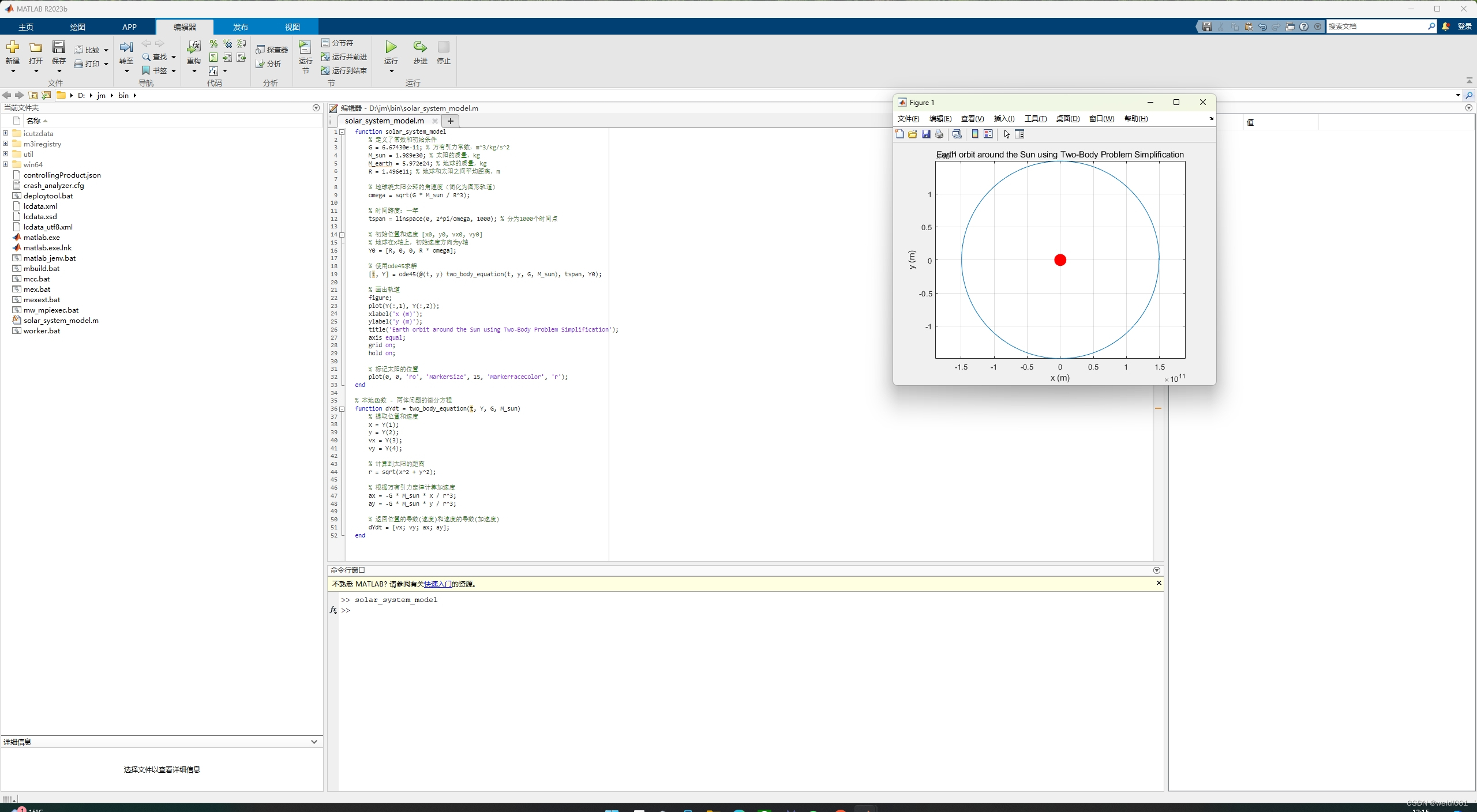

 

        在这个模型中，我们使用的ode45求解器是基于Runge-Kutta方法的，适用于求解非刚性微分方程。它在科学和工程领域的数学建模中非常普遍，因为许多物理过程都可通过常微分方程进行描述。

        此模型的输出是绘制了地球在一年内绕太阳运行的轨迹图。它非常直观地展示了MATLAB在数学建模方面的可视化和计算能力。

结论

        MATLAB提供了一个用户友好、功能强大的环境，使数学建模既便捷又精确。它允许用户从最简单的线性模型到最复杂的动态系统模型，覆盖各种数学建模的需求。无论是学术研究还是工程实践，MATLAB都不可或缺。通过掌握编程和算法开发技能，并深入理解研究领域的数学和物理原理，学习和实践是发挥MATLAB全部潜力的关键。

附：进阶模型

function solar_system_model% 定义太阳的质量和万有引力常数G = 6.67430e-11; % m^3/kg/s^2M_sun = 1.989e30; % kg% （此处省略了前面已经提供的定义行星质量的代码）% 定义行星的初始位置和速度（以下的位置和速度数据应从天文资料获取精确值）% 地球R_earth = 1.496e11; % mV_earth = 29.78e3; % m/s% 水星 MercuryR_mercury = 5.79e10; % mV_mercury = 47.87e3; % m/s% 金星 VenusR_venus = 1.082e11; % mV_venus = 35.02e3; % m/s% 火星 MarsR_mars = 2.279e11; % mV_mars = 24.07e3; % m/s% 考虑椭圆轨道，初始化位置需要调整，以下是简化的圆形轨道% 时间跨度：一年，足够长以观察行星运动tspan = [0, 365*24*3600]; % 以秒为单位% 初始化位置和速度向量（此处省略初始化其他行星的代码）% 初始时刻假设所有行星都在太阳的右侧，并沿着y轴方向运动init_conditions = [R_mercury, 0, 0, V_mercury, % 水星R_venus, 0, 0, V_venus, % 金星R_earth, 0, 0, V_earth, % 地球R_mars, 0, 0, V_mars, % 火星% 为木星、土星、天王星、海王星添加初始条件...];% 使用ode45求解器进行数值积分options = odeset('RelTol', 1e-5, 'AbsTol', 1e-6);[t, Y] = ode45(@(t, y) n_body_problem(t, y, G, M_sun, M_mercury, M_venus, M_earth, M_mars), tspan, init_conditions, options);% 绘制位置和轨道的后续代码（此处省略）
end% N体问题的微分方程
function dYdt = n_body_problem(t, Y, G, M_sun, M_mercury, M_venus, M_earth, M_mars)% 提取各个行星的位置和速度x_mercury = Y(1); y_mercury = Y(2); vx_mercury = Y(3); vy_mercury = Y(4);x_venus = Y(5); y_venus = Y(6); vx_venus = Y(7); vy_venus = Y(8);x_earth = Y(9); y_earth = Y(10); vx_earth = Y(11); vy_earth = Y(12);x_mars = Y(13); y_mars = Y(14); vx_mars = Y(15); vy_mars = Y(16);% 为木星、土星、天王星、海王星添加位置和速度变量...% 计算太阳对每个行星的引力作用% 对于水星Mercuryr_mercury = sqrt(x_mercury^2 + y_mercury^2);ax_mercury = -G * M_sun * x_mercury / r_mercury^3;ay_mercury = -G * M_sun * y_mercury / r_mercury^3;% 对于金星Venusr_venus = sqrt(x_venus^2 + y_venus^2);ax_venus = -G * M_sun * x_venus / r_venus^3;ay_venus = -G * M_sun * y_venus / r_venus^3;% 对于地球Earthr_earth = sqrt(x_earth^2 + y_earth^2);ax_earth = -G * M_sun * x_earth / r_earth^3;ay_earth = -G * M_sun * y_earth / r_earth^3;% 对于火星Marsr_mars = sqrt(x_mars^2 + y_mars^2);ax_mars = -G * M_sun * x_mars / r_mars^3;ay_mars = -G * M_sun * y_mars / r_mars^3;% 为木星、土星、天王星、海王星添加加速度计算...% 计算行星间的引力作用(略)% 将速度和加速度组合成导数向量返回dYdt = [vx_mercury; vy_mercury; ax_mercury; ay_mercury;vx_venus;   vy_venus;   ax_venus;   ay_venus;vx_earth;   vy_earth;   ax_earth;   ay_earth;vx_mars;    vy_mars;    ax_mars;    ay_mars;% 为木星、土星、天王星、海王星添加导数...];
end