文心一言
ReLU(Rectified Linear Unit)函数是深度学习领域中常用的一种激活函数。它具有简单、计算高效且在某些情况下能有效缓解梯度消失问题等优点,因此在神经网络中得到了广泛的应用。
ReLU函数的定义非常简单,其数学表达式为:
f(x) = max(0, x)
这意味着对于输入x,如果x大于0,则输出x;如果x小于或等于0,则输出0。因此,ReLU函数在输入为正数时保持了线性关系,而在输入为非正数时则输出0,使得神经元在此时处于“失活”状态。
ReLU函数在深度学习中具有以下几个优点:
- 计算高效:ReLU函数只需要进行简单的比较和乘法操作,计算速度非常快,适合用于大规模神经网络。
- 缓解梯度消失问题:在深度神经网络中,由于链式法则的作用,梯度在反向传播过程中可能会逐渐消失,导致模型训练困难。而ReLU函数在输入为正数时具有恒定的导数(1),有助于缓解这一问题。
- 稀疏性:ReLU函数使得神经元在输入为非正数时处于失活状态,从而实现了神经网络的稀疏性。这有助于提取数据的特征并降低过拟合的风险。
然而,ReLU函数也存在一些缺点,例如:
- 死亡ReLU问题:在训练过程中,如果某个神经元的输入始终为负,那么该神经元将永远不会被激活,导致权重无法更新。这被称为“死亡ReLU”问题。为了解决这个问题,可以使用一些改进版本的ReLU函数,如Leaky ReLU、Parametric ReLU等。
- 对输入数据的敏感性:ReLU函数对输入数据的分布较为敏感。如果输入数据的均值和方差较大,可能会导致大量的神经元失活,影响模型的性能。因此,在实际应用中,通常需要对输入数据进行归一化处理。
总之,ReLU函数作为深度学习领域的一种重要激活函数,具有广泛的应用价值。在实际应用中,需要根据具体任务和数据特点选择合适的激活函数,以优化模型的性能。
智谱清言
ReLU(Rectified Linear Unit,修正线性单元)是一种在深度学习中常用的激活函数,其目的是引入非线性因素,使得神经网络能够学习更加复杂的特征和函数。

ReLU函数有以下几个重要性质:
- 非线性:ReLU函数引入了非线性因素,使得神经网络可以捕捉到非线性关系。
- 简单有效:ReLU函数简单易实现,并且在训练深度神经网络时能够提供不错的性能。
- 梯度消失和梯度爆炸问题:与传统的Sigmoid或Tanh函数相比,ReLU函数在反向传播时不会出现梯度消失或梯度爆炸问题,因为对于正数,梯度为1,而对于零或负数,梯度为0,因此可以有效地缓解梯度消失问题。
- 资源占用少:由于ReLU函数的输出要么是输入的值,要么是零,所以对于激活层的每个神经元,只需要存储一个值,大大减少了模型的参数和计算量。
ReLU函数通常被用在神经网络的隐藏层,而在输出层,由于需要得到具体的类别标签或数值输出,通常不会使用ReLU函数,而会使用如Sigmoid、Tanh或线性激活函数。
豆包
ReLU(Rectified Linear Unit)函数是深度学习中常用的激活函数之一。它的全称为修正线性单元,其函数表达式为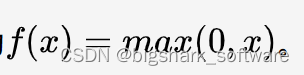 。
。
ReLU 函数的主要特点是简单、计算效率高,并能够在一定程度上缓解梯度消失问题。当输入值为正数时,ReLU 函数的输出值等于输入值本身;当输入值为负数时,输出值为零。
相较于传统的 sigmoid 或 tanh 激活函数,ReLU 函数具有以下优点:
- 计算简单:ReLU 函数不需要进行复杂的指数运算,计算速度快,适用于大规模数据的处理。
- 缓解梯度消失:当输入值为负数时,ReLU 函数的导数为零,这有助于防止在反向传播过程中梯度消失的问题,从而加快模型的训练速度。
- 具有稀疏性:ReLU 函数使得大量的神经元输出为零,从而实现了网络的稀疏性,减少了参数数量,提高了模型的泛化能力。
然而,ReLU 函数也存在一些潜在的问题,例如可能导致神经元死亡(ReLU 神经元在训练过程中不再对后续的训练数据产生响应)。为了缓解这个问题,一些改进的 ReLU 函数,如 Leaky ReLU、PReLU 等被提出。
总的来说,ReLU 函数在深度学习中被广泛应用,并且在许多情况下是一种有效的激活函数选择。但在实际应用中,需要根据具体问题和模型结构选择合适的激活函数。
讯飞星火
ReLU函数,全称为修正线性单元(Rectified Linear Unit),是深度学习中常用的一种激活函数。它的主要作用是在神经网络中引入非线性因素,帮助网络学习复杂的数据模式。
ReLU函数的定义非常简单:对于输入的数值x,如果x大于等于0,则输出为x本身;如果x小于0,则输出为0。这种特性使得ReLU函数在处理正数时保持线性,而在处理负数时将其置零,从而有效地增加了模型的非线性表达能力。
以下是关于ReLU函数的一些特点:
- 计算效率高:ReLU函数的计算非常简单,只需要一个阈值判断,这使得它在前向传播和反向传播时的计算效率非常高。
- 稀疏激活性:由于ReLU函数在输入值为负时输出为零,这导致了网络的一部分神经元不会被激活,从而产生稀疏的激活模式,这有助于模拟大脑神经元的工作方式。
- 缓解梯度消失问题:ReLU函数在一定程度上有助于缓解梯度消失问题,这是因为它的导数在输入值大于0时恒为1,这意味着在进行反向传播时,梯度不会因为多层传递而衰减得太严重。
- 死亡ReLU问题:ReLU函数也存在一些问题,比如所谓的“死亡ReLU”问题,即一旦某个神经元的输入落入负值区间,该神经元将不再对任何数据做出反应,导致模型学习不充分。
- 变种:为了解决ReLU函数的问题,研究者们提出了一些改进的版本,如Leaky ReLU、Parametric ReLU和Exponential LU等,这些变种在不同程度上改善了ReLU函数的性能。
总的来说,ReLU函数因其简单性和高效性在深度学习领域得到了广泛应用,尽管存在一些缺点,但它仍然是许多神经网络架构中默认的激活函数选择。