1、思路讲解（LC704）

LC704：给定一个长度为$n$的数组 nums ，元素按从小到大的顺序排列且不重复。请查找并返回元素 target 在该数组中的索引。若数组不包含该元素，则返回-1。

暴力法思路： 从$nums[0]$开始遍历一遍，time complexity = $O(n)$
二分法思路：
☀️首先要保证原序列是排好顺序的

2、代码思路讲解（循环不变量）

伪代码：

def func(nums , target) -> int:# 初始化首元素、尾元素left = 0right = len(nums) - 1 or len(nums)# 循环while 满足左指针在右指针的左边:# 理论上 Python 的数字可以无限大（取决于内存大小），无须考虑大数越界问题m = (i + j) // 2  # 计算中点索引 mif nums[m] < target:# 说明target在nums[m]的右侧移动leftelif nums[m] > target:# 说明target在nums[m]的左侧else:return m  # 找到目标元素，返回其索引return -1  # 未找到目标元素，返回 -1

这里面有几个很容易出错的点（会导致循环不收敛
）：

• while的循环条件是：$left<=right$ or $left<right$
• 当nums[mid]<target的时候，应该是$left=mid+1$ or $left=mid$
• 当nums[mid]>target的时候，应该是$right=mid-1$ or $right=mid$
  这几个问题的答案是：你定义的区间是什么样子的？

（1） 左闭右闭

如果定义的区间是左闭右闭的情况：$[left,right]$

• while的循环条件是：$left<=right$ （⭐️最推荐的选择，so easy）
  • 因为当 $left=right$ 的时候，$[left,right]$区间中仍然有一个元素，所以仍然是合法的
• 当nums[mid]<target的时候，应该是$left=mid+1$
  • 因为当nums[mid]<target的时候，就证明了mid指向的值一定不是目标值，所以left不应该指向mid，而应该是mid+1
• 当nums[mid]>target的时候，应该是$right=mid-1$ or $right=mid$

def binary_search(nums: list[int], target: int) -> int:"""二分查找（双闭区间）"""# 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素i, j = 0, len(nums) - 1# 循环，当搜索区间为空时跳出（当 i > j 时为空）while i <= j:# 理论上 Python 的数字可以无限大（取决于内存大小），无须考虑大数越界问题m = (i + j) // 2  # 计算中点索引 mif nums[m] < target:i = m + 1  # 此情况说明 target 在区间 [m+1, j] 中elif nums[m] > target:j = m - 1  # 此情况说明 target 在区间 [i, m-1] 中else:return m  # 找到目标元素，返回其索引return -1  # 未找到目标元素，返回 -1

（2）左闭右开

如果定义的区间是左闭右开的情况：$[left,right)$

• while的循环条件是：$left<right$
  • 因为当 $left=right$ 的时候，$[left=right,right)$区间就会既有right又没有right，这种情况显然是不合法的
• 当nums[mid]<target的时候，应该是$left=mid+1$
  • 因为当nums[mid]<target的时候，就证明了mid指向的值一定不是目标值，所以left不应该指向mid，而应该是mid+1
• 当nums[mid]>target的时候，应该是 $right=mid$
  • 因为区间是$[left,right)$，当mid的值不是目标值的时候，区间应该是mid值前面的序列，但是因为右区间是开区间，所以可以直接将right指向mid。

def binary_search_lcro(nums: list[int], target: int) -> int:"""二分查找（左闭右开区间）"""# 初始化左闭右开区间 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1i, j = 0, len(nums)# 循环，当搜索区间为空时跳出（当 i = j 时为空）while i < j:m = (i + j) // 2  # 计算中点索引 mif nums[m] < target:i = m + 1  # 此情况说明 target 在区间 [m+1, j) 中elif nums[m] > target:j = m  # 此情况说明 target 在区间 [i, m) 中else:return m  # 找到目标元素，返回其索引return -1  # 未找到目标元素，返回 -1

（3）总结：左开右闭和左闭右开

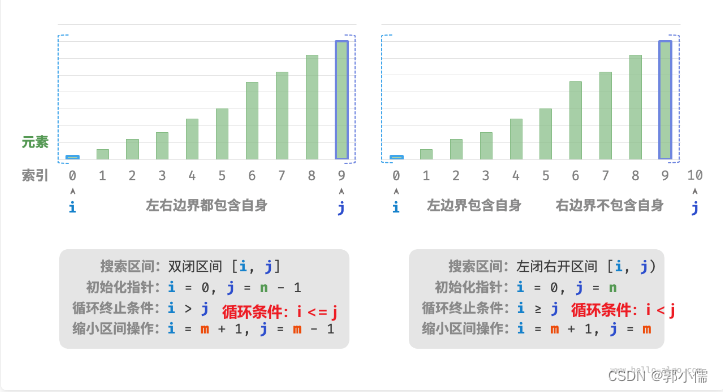
（4）复杂度分析

时间复杂度：$O(logn)$ 每次循环区间减少一半，因此循环次数是$O(logn)$
空间复杂度：$O(1)$没用使用数组啥的

3. 习题分析

（1）LC35 搜索插入位置 easy （二分查找法变种问题）

LC35：给定一个长度为$n$的数组 nums ，元素按从小到大的顺序排列且不重复。给一个元素target，想要插入到nums中，并保持有序性。如果数组中存在target，就将targat插入到左侧；如果不存在，将target插入到按顺序插入的位置，返回索引。

思路

⭐️思考：
Q1： 当数组中有target的时候，插入点的索引是否就是返回值？
回答： yep！当查找到原数组有target值时，新的target要放在老的target的左侧，也就是说新的target代替了老的target的位置，也就是插入点的索引就是新插入的target的索引
Q2： 当数组不存在target的时候，新插入点是哪个元素的索引？

代码

def binary_search_insertion_simple(nums: list[int], target: int) -> int:"""二分查找插入点（无重复元素）闭区间"""i, j = 0, len(nums) - 1  # 初始化双闭区间 [0, n-1]while i <= j:m = (i + j) // 2  # 计算中点索引 mif nums[m] < target:i = m + 1  # target 在区间 [m+1, j] 中elif nums[m] > target:j = m - 1  # target 在区间 [i, m-1] 中else:return m  # 找到 target ，返回插入点 m# 未找到 target ，返回插入点 ireturn i

（2）LC34 在排序数组中查找元素的第一个和最后一个位置 medium（有重复元素的情况）

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target，返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

思路1：二分查找+线性遍历

1️⃣ 执行二分查找，得到任意一个 target 的索引
2️⃣从找到的这个索引开始，分别向左和向右遍历，找到start和end指针

class Solution:def searchRange(self, nums: List[int], target: int) -> List[int]:if nums is None or len(nums) == 0:return [-1,-1]# 先用二分查找法找到target# 双闭区间（有重复元素）left = 0right = len(nums) - 1flag = 0while left <= right:mid = left + (right - left) // 2if target > nums[mid]: # 应该删除前半部分的元素left = mid + 1elif target < nums[mid]: # 应该删除后半部分的元素right = mid - 1else: # 当找到其中一个目标值之后，分别向前和向后遍历，找到起始和终止位置flag = 1start = midend = midwhile start >= 0 and nums[start] == target:start -= 1while end <= len(nums)-1 and nums[end] == target:end += 1breakif flag == 1:return [start+1,end-1]else:return [-1,-1]

时间复杂度： $O(n)$，数组中存在很多重复的 target 时，该方法效率很低。

思路2：扩展二分查找

1️⃣查找左边界

• 查找到任意一个target
• 左边界$start$必定在 $[left,mid-1]$中，所以可以将 $right=mid-1$，缩小区间，重新搜索一个新的target，新的target必定在源target的左侧
• 因为想要最左侧target的索引，所以和LC704是一样的，最后返回的是$start=mid$

2️⃣查找右边界

class Solution:def searchRange(self, nums: List[int], target: int) -> List[int]:if nums is None or len(nums) == 0:return [-1,-1]# 扩展二分查找法：查找target时候使用二分查找法，确定边界的时候仍然使用二分查找法# 先用二分查找法找到左边界# 双闭区间（有重复元素）left = 0right = len(nums) - 1start = -1while left <= right:mid = left + (right - left) // 2if target > nums[mid]: # 应该删除前半部分的元素left = mid + 1elif target < nums[mid]: # 应该删除后半部分的元素right = mid - 1else: # 当找到其中一个目标值之后# 左边界start应该在[left,mid]之间right = mid - 1start = mid# 再用二分查找法找到右边界left = 0right = len(nums) - 1end = -1while left <= right:mid = left + (right - left) // 2if target > nums[mid]: # 应该删除前半部分的元素left = mid + 1elif target < nums[mid]: # 应该删除后半部分的元素right = mid - 1else: # 当找到其中一个目标值之后# 右边界end应该在[mid,right]之间left = mid + 1end = mid     return [start,end]   

时间复杂度： $O(logN)$