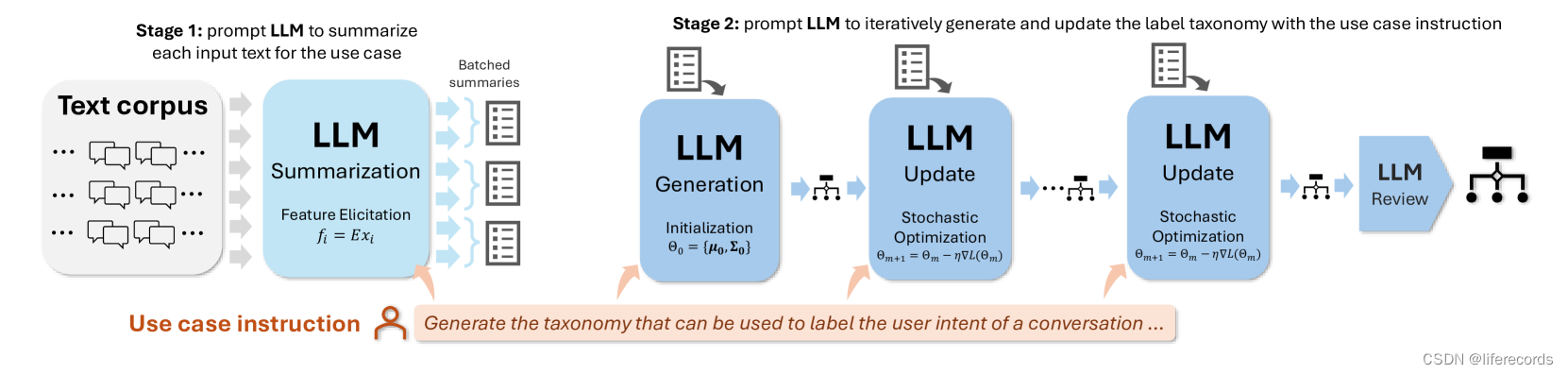
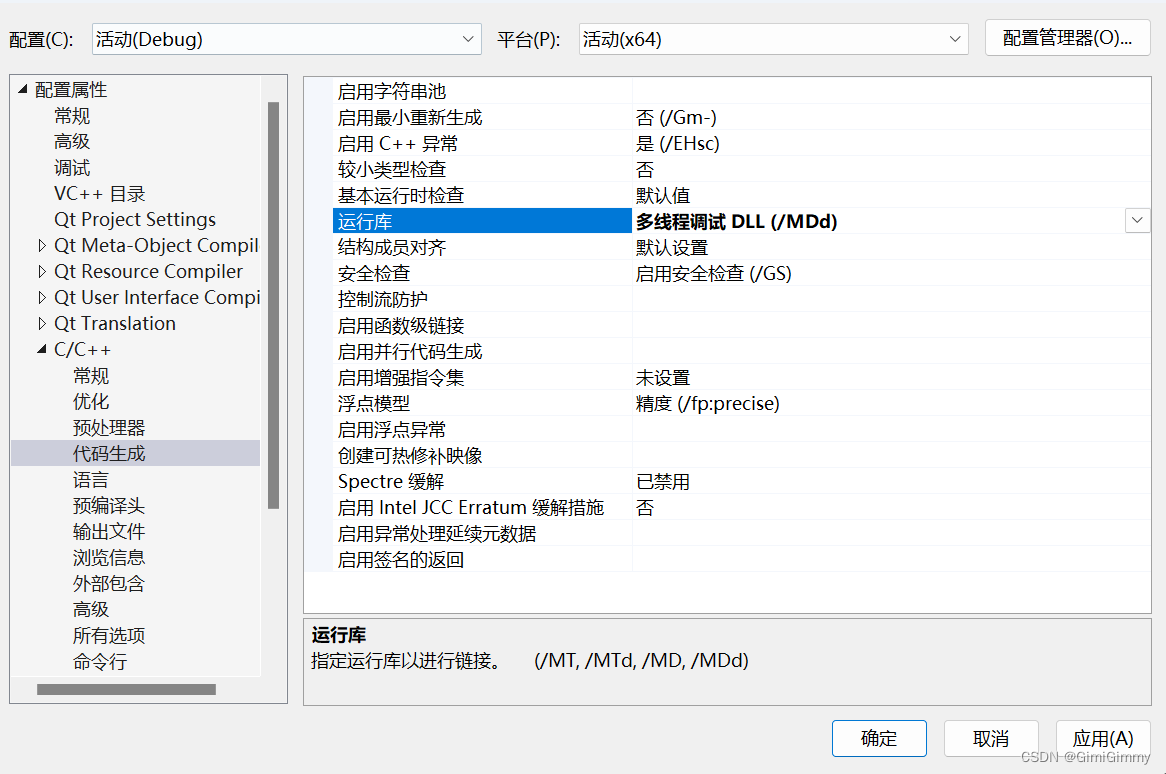
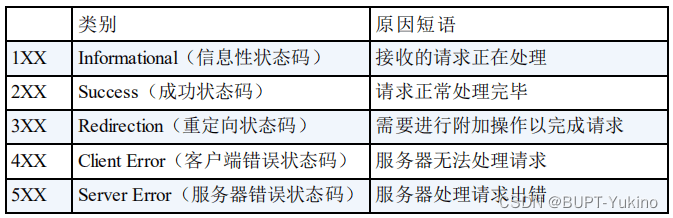
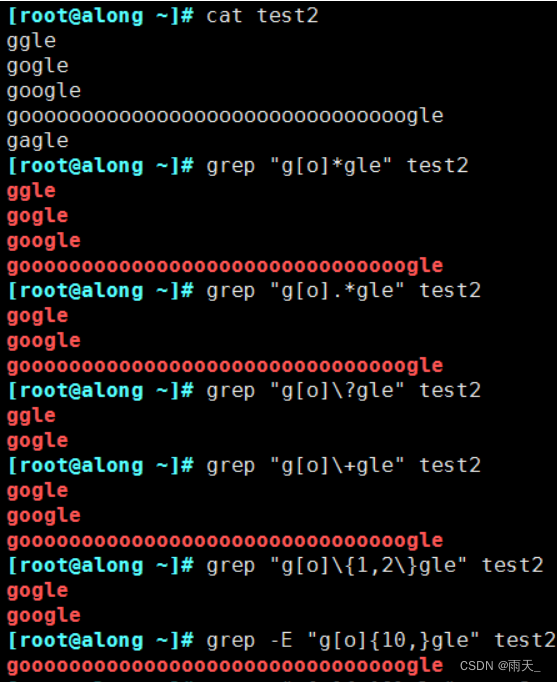
介绍：

在线性神经网络中，线性回归是一种常见的任务，用于预测一个连续的数值输出。其目标是根据输入特征来拟合一个线性函数，使得预测值与真实值之间的误差最小化。

线性回归的数学表达式为：
y = w1x1 + w2x2 + ... + wnxn + b

其中，y表示预测的输出值，x1, x2, ..., xn表示输入特征，w1, w2, ..., wn表示特征的权重，b表示偏置项。

训练线性回归模型的目标是找到最优的权重和偏置项，使得模型预测的输出与真实值之间的平方差（即损失函数）最小化。这一最优化问题可以通过梯度下降等优化算法来解决。

线性回归在深度学习中也被广泛应用，特别是在浅层神经网络中。在深度学习中，通过将多个线性回归模型组合在一起，可以构建更复杂的神经网络结构，以解决更复杂的问题。

 手动生成数据集：

%matplotlib inline
import torch
from d2l import torch as d2l
import random#"""生成y=Xw+b+噪声"""
def synthetic_data(w, b, num_examples):  #生成num_examples个样本X = d2l.normal(0, 1, (num_examples, len(w)))#随机x,长度为特征个数，权重个数y = d2l.matmul(X, w) + b#y的函数y += d2l.normal(0, 0.01, y.shape)#加上0~0.001的随机噪音return X, d2l.reshape(y, (-1, 1))#返回true_w = d2l.tensor([2, -3.4])#初始化真实w
true_b = 4.2#初始化真实bfeatures, labels = synthetic_data(true_w, true_b, 1000)#随机一些数据
print(features)
print(labels)

显示数据集：

print('features:', features[0],'\nlabel:', labels[0])'''
features: tensor([ 2.1714, -0.6891]) 
label: tensor([10.8673])
'''d2l.set_figsize()
d2l.plt.scatter(d2l.numpy(features[:, 1]), d2l.numpy(labels), 1);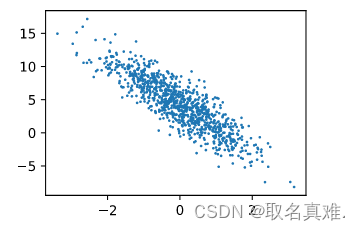

读取小批量数据集：

#每次抽取一批量样本
def data_iter(batch_size, features, labels):#步长、特征、标签num_examples = len(features)#特征个数indices = list(range(num_examples))random.shuffle(indices)# 这些样本是随机读取的，没有特定的顺序，打乱顺序for i in range(0, num_examples, batch_size):#随机访问，步长为batch_sizebatch_indices = d2l.tensor(indices[i: min(i + batch_size, num_examples)])yield features[batch_indices], labels[batch_indices]

定义模型：

#定义模型
def linreg(X, w, b):  """线性回归模型"""return d2l.matmul(X, w) + b

定义损失函数：

#定义损失和函数
def squared_loss(y_hat, y):  #@save"""均方损失"""return (y_hat - d2l.reshape(y, y_hat.shape)) ** 2 / 2

定义优化算法（小批量随机梯度下降）：

#定义优化算法  """小批量随机梯度下降"""
def sgd(params, lr, batch_size):  #参数、lr学习率、with torch.no_grad():for param in params:param -= lr * param.grad / batch_sizeparam.grad.zero_()

模型训练：

#训练
lr = 0.03#学习率
num_epochs = 3#数据扫三遍
net = linreg#模型
loss = squared_loss#损失函数
#初始化模型参数
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)#权重
b = torch.zeros(1, requires_grad=True)#b全赋为0for epoch in range(num_epochs):for X, y in data_iter(batch_size, features, labels):#拿出一批量x，yl = loss(net(X, w, b), y)  # X和y的小批量损失,实际的和预测的# 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，# 并以此计算关于[w,b]的梯度l.sum().backward()sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数with torch.no_grad():train_l = loss(net(features, w, b), labels)print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
'''
epoch 1, loss 0.037302
epoch 2, loss 0.000140
epoch 3, loss 0.000048
'''print(f'w的估计误差: {true_w - d2l.reshape(w, true_w.shape)}')
print(f'b的估计误差: {true_b - b}')
'''
w的估计误差: tensor([0.0006, 0.0001], grad_fn=<SubBackward0>)
b的估计误差: tensor([-0.0003], grad_fn=<RsubBackward1>)
'''print(w)
'''
tensor([[ 1.9994],[-3.4001]], requires_grad=True)
'''print(b)
'''
tensor([4.2003], requires_grad=True)
'''