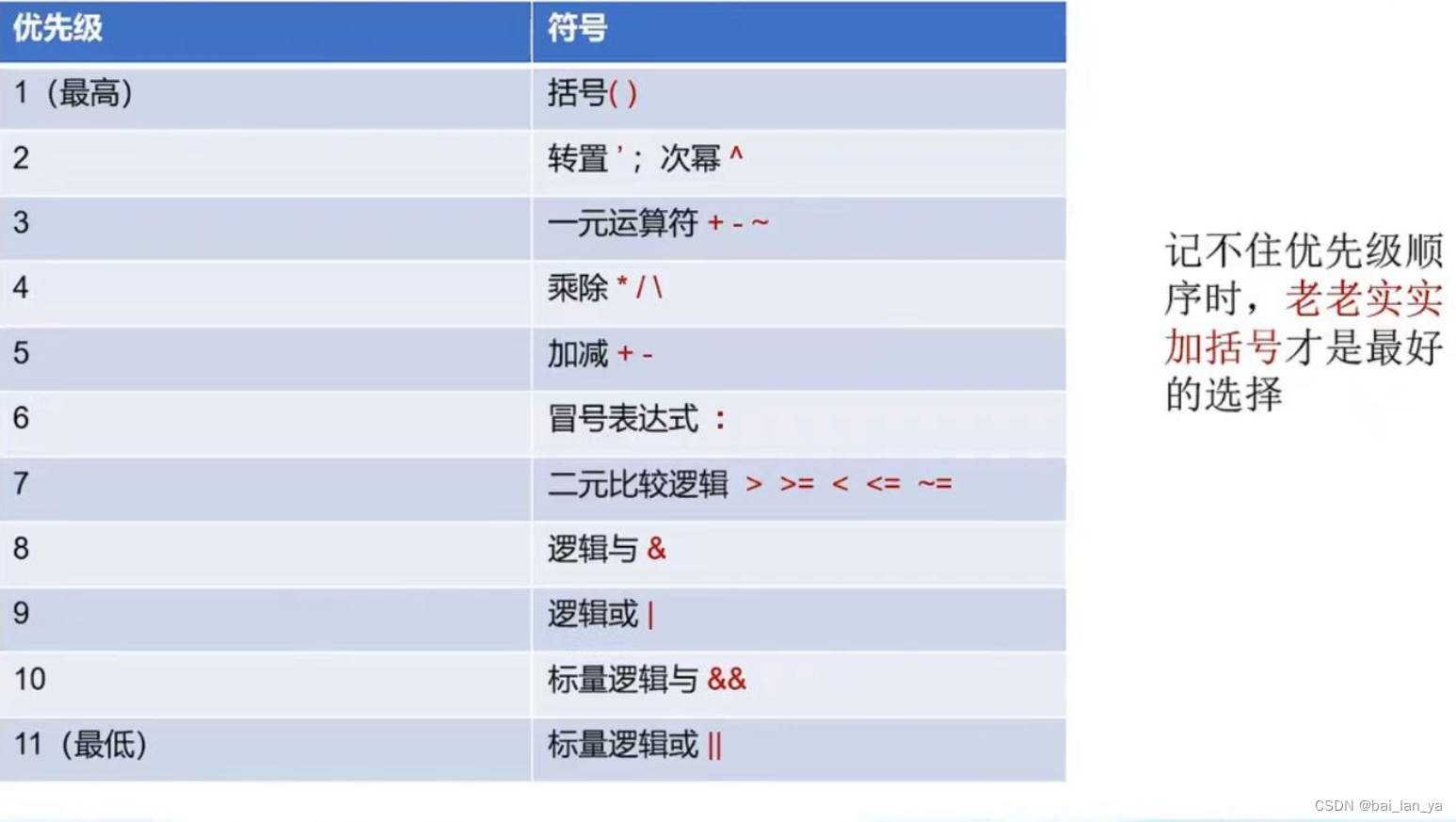
目录

斐波那契数列模型  

1. 第N个泰波那契数

 2.使用最小花费爬楼梯

3.解码方法 

---

         学过算法的应该知道，动态规划一直都是一个非常难的模块，无论是状态转移方程的定义还是dp表的填表，都非常难找到思路。在这个算法的支线专题中我会结合很多力扣题型，由简单到复杂，带大家深度剖析动态规划类的题型，欢迎大家关注啊。

顺序：

题目链接-》算法思路-》代码呈现

斐波那契数列模型  

动态规划类题目解题步骤：

1. 依据题目进行状态表示(dp[i]的含义)
2. 写出状态转移方程(类似于dp[i]=dp[i-1]+dp[i-2])
3. 为防止填表时数组越界，对dp表进行初始化（dp[0]=dp[1]=1）
4. 搞清楚填表顺序（从前往后或者从后往前）
5. 利用dp表返回问题答案

1. 第N个泰波那契数

题目链接：

https://leetcode.cn/problems/n-th-tribonacci-number/description/

算法思路：

代码呈现：

class Solution {public int tribonacci(int n) {if(n==0){return 0;}if(n==1||n==2){return 1;}int[] dp=new int[n+1];dp[0]=0;dp[1]=1;dp[2]=1;for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2]+dp[i-3];}return dp[n];}
}

 2.使用最小花费爬楼梯

题目链接：

https://leetcode.cn/problems/min-cost-climbing-stairs/description/

算法思路：

代码呈现：

class Solution {public int minCostClimbingStairs(int[] cost) {int size=cost.length;if(size==2) return Math.min(cost[0],cost[1]);int[] dp=new int[size+1];dp[0]=0;dp[1]=0;dp[2]=Math.min(cost[0],cost[1]);for(int i=3;i<=size;i++){dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[size];}
}

3.解码方法 

题目链接：

https://leetcode.cn/problems/decode-ways/

 算法思路：

• 让 i 位置上的数单独解码成⼀个字⺟，就存在「解码成功」和「解码失败」两种情况：

i. 解码成功：当 i 位置上的数在 [1, 9] 之间的时候，说明 i 位置上的数是可以单独解 码的，那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 1] 区间上的解码⽅ 法。因为 [0, i - 1] 区间上的所有解码结果，后⾯填上⼀个 i 位置解码后的字⺟就 可以了。此时 dp[i] = dp[i - 1] ；

ii. 解码失败：当 i 位置上的数是 0 的时候，说明 i 位置上的数是不能单独解码的，那么此时 [0, i] 区间上不存在解码⽅法。因为 i 位置如果单独参与解码，但是解码失败了，那么前⾯做的努⼒就全部⽩费了。此时 dp[i] = 0 。

代码呈现：

class Solution {public int numDecodings(String s) {char[] arr=s.toCharArray();int n=arr.length;int[] dp=new int[n+1];dp[0]=1;if(arr[0]=='0') dp[1]=0;else dp[1]=1;if(n==1){return dp[1];}for(int i=2;i<n+1;i++){if(arr[i-1]!='0'){dp[i]+=dp[i-1];}if(((arr[i-2]-'0')*10+(arr[i-1]-'0'))<=26&&((arr[i-2]-'0')*10+(arr[i-1]-'0'))>=10){dp[i]+=dp[i-2];}}return dp[n];}
}