论文标题:TimeMixer: Decomposable Multiscale Mixing for Time Series Forecasting
作者:Shiyu Wang(王世宇), Haixu Wu(吴海旭), Xiaoming Shi, Tengge Hu, Huakun Luo, Lintao Ma, James Y. Zhang, and Jun Zhou
机构:蚂蚁集团,清华大学
论文发表:[ICLR 2024]The Twelfth International Conference on Learning Representations
论文链接:https://openreview.net/forum?id=7oLshfEIC2
代码:https://github.com/kwuking/TimeMixer
TL; DR:TimeMixer是一种基于多尺度融合架构的时序预测模型,它通过解耦多尺度时间序列的过去信息和未来预测,实现了在长期和短期预测任务上的卓越性能和效率。
关键词:时序预测,多尺度融合,长时预测,解耦,MLP
原文解读链接:论文精读 | 2024 [ICLR] TimeMixer: 可分解多尺度融合的时间序列预测

🌟【紧跟前沿】“时空探索之旅”与你一起探索时空奥秘!🚀
欢迎大家关注时空探索之旅
摘要
TimeMixer模型针对时间序列预测的复杂性提出了一个多尺度混合架构,旨在利用过去可分解混合(PDM)模块提取过去的关键信息,并通过未来多预测器混合(FMM)模块进行未来序列的预测。具体来说,TimeMixer首先通过平均下采样生成多尺度观测,然后PDM采用可分解设计更好地处理季节性和趋势变化的不同属性,通过在精细到粗略和粗略到精细方向上分别混合多尺度季节性和趋势组件。FMM在预测阶段集成多个预测器,利用多尺度观测中的互补预测能力。该模型在多个长期和短期预测任务中均实现了一致的最先进性能,并在所有实验中展现出卓越的效率。
主要工作和创新点
- 多尺度混合视角: 论文从一种新的多尺度混合视角来处理时间序列预测中的复杂时间变化,利用解耦变化和来自多尺度序列的互补预测能力。
- 简单但有效的预测模型: 论文提出了TimeMixer模型,它在历史信息提取和未来预测阶段都能结合多尺度信息,这得益于论文量身定制的可分解和多预测器混合技术。
- 在广泛基准上的一致最先进性能: TimeMixer在一系列广泛的基准测试中实现了长期和短期预测任务的一致最先进性能,并在所有实验中展现出卓越的效率 。
模型框架
-
TimeMixer模型采用了一个多尺度混合架构,旨在解决时间序列预测中的复杂时间变化问题。该模型主要采用全MLP(多层感知机)架构,由过去可分解混合 (PDM) 和未来多预测器混合 (FMM) 两大块构成,能够有效利用多尺度序列信息。
-
PDM负责提取过去的信息并将不同尺度上的季节性和趋势组分分别混合。
-
FMM通过集成多个预测器(主要是)的方式来提高未来序列的预测准确性,每个预测器都基于不同尺度上的信息进行预测。
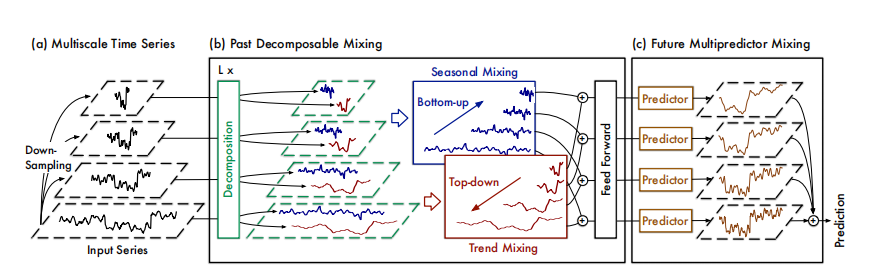
首先对过去的观察数据 x ∈ R P × C x \in \mathbb{R}^{P \times C} x∈RP×C进行下采样,通过平均池化最终得到多尺度时间序列的集合 X = { x 0 , … , x M } \mathcal{X} = \{x_0, \ldots, x_M\} X={x0,…,xM},其中 x m ∈ R P 2 m × C x_m \in \mathbb{R}^{\frac{P}{2^m} \times C} xm∈R2mP×C, m ∈ { 0 , … , M } m \in \{0, \ldots, M\} m∈{0,…,M}, C C C 表示变量的数量。最低级别的序列 x 0 = x x_0 = x x0=x 是输入序列,包含最精细的时间变化,而最高级别的序列 x M x_M xM 代表宏观变化。然后将这些多尺度序列投射到嵌入层得到深层特征 X ( 0 ) \mathcal{X}^{(0)} X(0),可以公式化为 X ( 0 ) = Embed ( X ) \mathcal{X}^{(0)} = \text{Embed}(\mathcal{X}) X(0)=Embed(X)。通过上述设计,得到了输入序列的多尺度表示。
接下来,利用堆叠的过去可分解混合(PDM)块来混合不同尺度的过去信息。对于第 L L L 层,输入是 X l − 1 \mathcal{X}^{l-1} Xl−1 并且 PDM 的过程可以公式化为:
X l = PDM ( X l − 1 ) , l ∈ { 0 , … , L } , \mathcal{X}^l = \text{PDM}(\mathcal{X}^{l-1}), \quad l \in \{0, \ldots, L\}, Xl=PDM(Xl−1),l∈{0,…,L},
其中 L L L是总层数,并且 X l = { x 0 l , … , x M l } , x m l ∈ R P 2 m × d model \mathcal{X}^l = \{x_0^l, \ldots, x_M^l\}, x_m^l \in \mathbb{R}^{\frac{P}{2^m} \times d_{\text{model}}} Xl={x0l,…,xMl},xml∈R2mP×dmodel 表示混合过去的表示,有 d model d_{\text{model}} dmodel 通道。
至于未来预测阶段,采用未来多预测器混合(FMM)块来整合提取的多尺度过去信息 X L \mathcal{X}^L XL 并生成未来预测,即:
x ^ = FMM ( X L ) , \hat{x} = \text{FMM}(\mathcal{X}^L), x^=FMM(XL),
其中 x ^ ∈ R F × C \hat{x} \in \mathbb{R}^{F \times C} x^∈RF×C 代表最终预测。通过上述设计,TimeMixer 能够成功捕捉到来自解开的多尺度观测的关键过去信息,并预测未来,从多尺度过去信息中获益。
PDM模块
通过过去分解混合(PDM)块,将分解的季节和趋势成分分别混合成多个尺度。
具体来说,对于第 l l l 个PDM块,首先将多尺度时间序列 X l \mathcal{X}^l Xl 分解为季节性部分 s l = s 0 l , … , s M l s^l = { s_0^l, \ldots, s_M^l } sl=s0l,…,sMl 和趋势部分 t l = t 0 l , … , t M l t^l = { t_0^l, \ldots, t_M^l } tl=t0l,…,tMl ,通过来自Autoformer(Wu et al., 2021)的序列分解块。考虑到季节趋势部分的独特属性,将混合操作应用于季节性和趋势术语,以分别与来自多个尺度的信息进行交互。总的来说,第 l l l 个PDM块可以被形式化为:
s m l , t m l = S e r i e s D e c o m p ( x m l ) , m ∈ { 0 , … , M } s_m^l, t_m^l = SeriesDecomp(x_m^l), m \in \{ 0, \ldots, M \} sml,tml=SeriesDecomp(xml),m∈{0,…,M}
x ′ l = x l − 1 + F e e d F o r w a r d ( S − M i x ( ( s m = 0 l ) M ) + T − M i x ( ( t m = 0 l ) M ) ) x'^l = x^l - 1 + FeedForward(S-Mix((s_{m=0}^l)^M) + T-Mix((t_{m=0}^l)^M)) x′l=xl−1+FeedForward(S−Mix((sm=0l)M)+T−Mix((tm=0l)M))
其中 F e e d F o r w a r d ( ⋅ ) FeedForward(\cdot) FeedForward(⋅) 包含两个线性层,中间有GELU激活函数,用于通道之间的信息互动。 S − M i x ( ⋅ ) S-Mix(\cdot) S−Mix(⋅), T − M i x ( ⋅ ) T-Mix(\cdot) T−Mix(⋅) 分别代表季节性和趋势混合。
-
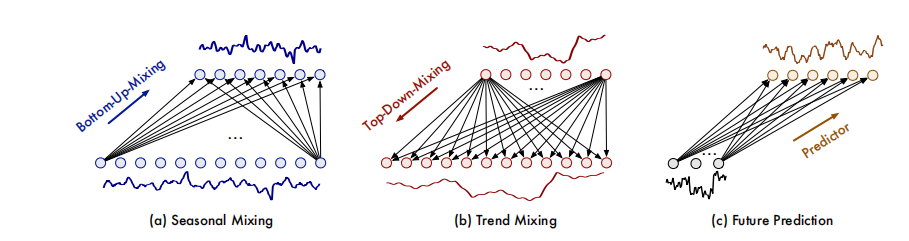
季节性混合:采用自下而上的方法,纳入低层次精细尺度时间序列的信息,可以为粗尺度的季节性建模补充详细信息。使用自底向上混合层在第 m 个尺度上以残差方式实现季节性信息的自底向上交互,可以被形式化为:
对于 m : 1 → M m: 1 \rightarrow M m:1→M 做: s m l = s m l + B o t t o m − U p − M i x i n g ( s m − 1 l ) s_m^l = s_m^l + Bottom-Up-Mixing(s_{m-1}^l) sml=sml+Bottom−Up−Mixing(sm−1l)。
其中 B o t t o m − U p − M i x i n g ( ⋅ ) Bottom-Up-Mixing(\cdot) Bottom−Up−Mixing(⋅) 被实例化为带有中间GELU激活函数的两个线性层,沿着时间维度,其输入维度是 ⌈ P 2 m ⌉ \left \lceil \frac{P}{2^m} \right \rceil ⌈2mP⌉,输出维度是 ⌊ P 2 m ⌋ \left \lfloor \frac{P}{2^m} \right \rfloor ⌊2mP⌋。
-
趋势混合: 针对趋势部分与季节性部分相反,趋势项的详细变化可能会引入噪声,影响宏观趋势的捕获。请注意,较高层次的粗尺度时间序列能够更容易地提供清晰的宏观信息。因此,采用自上而下的混合方法,利用来自粗尺度的宏观知识来指导细尺度的趋势建模。
技术上,对于多尺度趋势组件 T l = { t 0 l , … , t M l } T^l = \{ t_0^l, \ldots, t_M^l \} Tl={t0l,…,tMl},我们采用自上而下的混合层在第 m m m 个尺度上以残差方式实现自上而下的趋势信息交互:
对于 m : ( M − 1 ) → 0 m: (M - 1) \rightarrow 0 m:(M−1)→0 做: t m l = t m l + T o p − D o w n − M i x i n g ( t m + 1 l ) t_m^l = t_m^l + Top-Down-Mixing(t_{m+1}^l) tml=tml+Top−Down−Mixing(tm+1l)。(5)
其中 T o p − D o w n − M i x i n g ( ⋅ ) Top-Down-Mixing(\cdot) Top−Down−Mixing(⋅) 是两个带有中间GELU激活函数的线性层,其输入维度是 ⌈ P 2 m + 1 ⌉ \left \lceil \frac{P}{2^m+1} \right \rceil ⌈2m+1P⌉,输出维度是 ⌊ P 2 m ⌋ \left \lfloor \frac{P}{2^m} \right \rfloor ⌊2mP⌋,受到季节性和趋势混合的赋能,PDM逐渐聚合详细的季节性信息从细到粗,并将宏观趋势信息与以往的先验知识融合,最终实现在过去信息提取中的多尺度混合。
FMM模块
在L个PDM块之后获得了多尺度过去的信息,表示为 X L = x 0 L , … , x M L ∈ R P × J × d m o d e l \mathcal{X}^L = {x_0^L, \ldots, x_M^L} \in \mathbb{R}^{P \times J \times d_{model}} XL=x0L,…,xML∈RP×J×dmodel。由于不同尺度的序列呈现出不同的主导变化,它们的预测也表现出不同的能力。为了充分利用这些多尺度信息,论文提出了一个聚合多尺度序列预测并呈现未来多预测器混合块的方法:
x ^ m = P r e d i c t o r m ( X m L ) , m ∈ { 0 , … , M } , x ^ = ∑ m = 0 M x ^ m , \hat{x}^m = Predictor_m(\mathcal{X}_m^L), m \in \{0, \ldots, M\}, \hat{x} = \sum_{m=0}^M \hat{x}_m, x^m=Predictorm(XmL),m∈{0,…,M},x^=∑m=0Mx^m,
其中 x ^ m ∈ R F × C \hat{x}_m \in \mathbb{R}^{F \times C} x^m∈RF×C 代表从第m尺度序列中的未来预测,最终输出是 x ^ ∈ R F × C \hat{x} \in \mathbb{R}^{F \times C} x^∈RF×C。 P r e d i c t o r m ( ⋅ ) Predictor_m(\cdot) Predictorm(⋅) 指的是第m尺度序列的预测器,首先采用单层线性层直接对长度为F的未来进行回归,从长度为 ⌈ P 2 m ⌉ \lceil \frac{P}{2^m} \rceil ⌈2mP⌉ 的过去信息中提取,然后将深层表示投影到C个变量上。注意FMM是一个集合体,不同的预测器基于来自不同尺度的过去信息,使得FMM能够整合混合多尺度序列的补充预测能力。
实验
长期预测数据集
- ETT(Electricity Transformer Temperature)数据集:包含4个子集(ETTh1, ETTh2, ETTm1, ETTm2),主要信息为温度,以15分钟为频率记录,预测长度为96至720。
- Weather:气象数据集,记录了21个变量,包括10分钟频率的气象信息,预测长度为96至720。
- Solar-Energy:太阳能发电数据集,包含137个变量,记录了10分钟频率的电力信息,预测长度为96至720。
- Electricity:电力消耗数据集,包含321个变量,记录了小时频率的电力信息,预测长度为96至720。
- Traffic:交通流量数据集,包含862个变量,记录了小时频率的交通信息,预测长度为96至720。
短期预测数据集
- PEMS(公共环境监测站)数据集:包含PEMS03、PEMS04、PEMS07和PEMS08四个公共交通网络数据集,分别记录了358、307、883和170个变量,预测长度为12,记录频率为5分钟。
- M4数据集:包含不同频率的100000个时间序列,涵盖小时、日、周、月、季度和年度频率,主要用于短期预测。
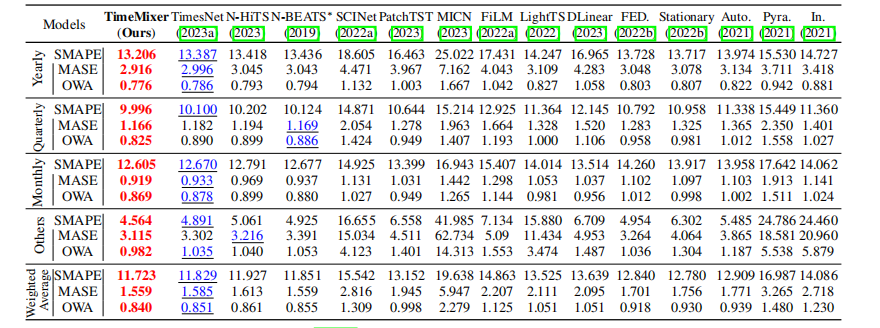
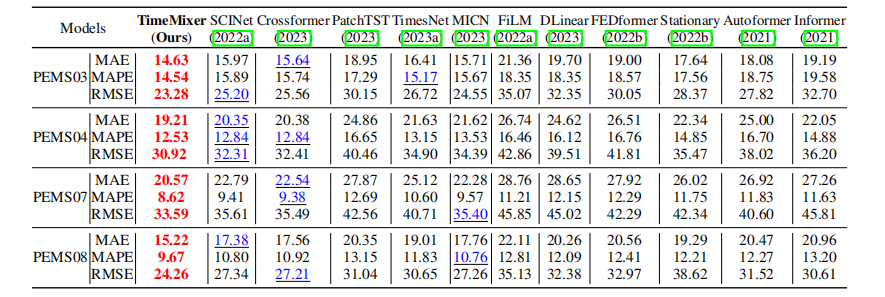
实验结果
长期结果

短期结果
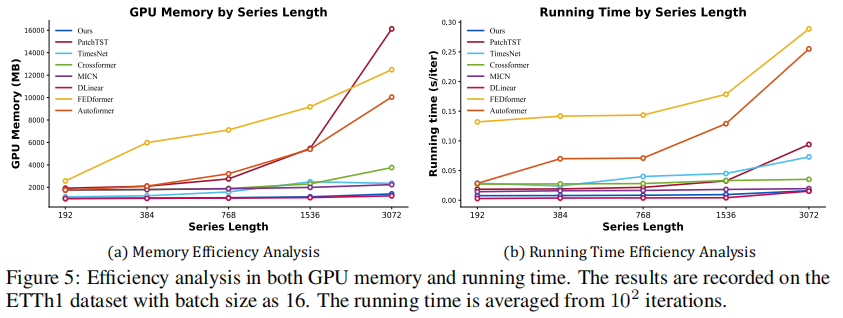
权重和效率分析
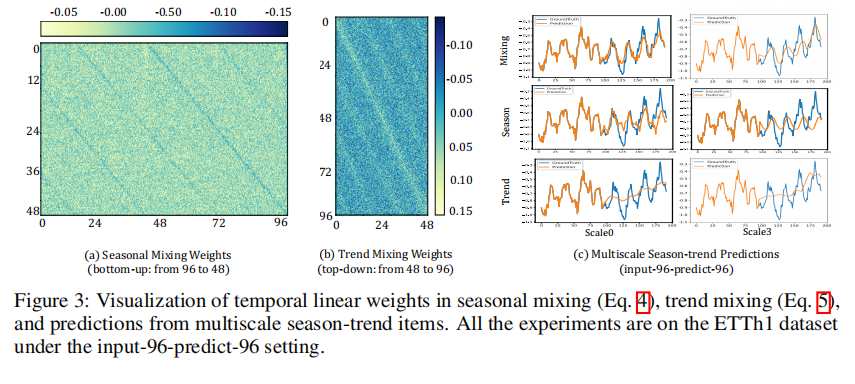
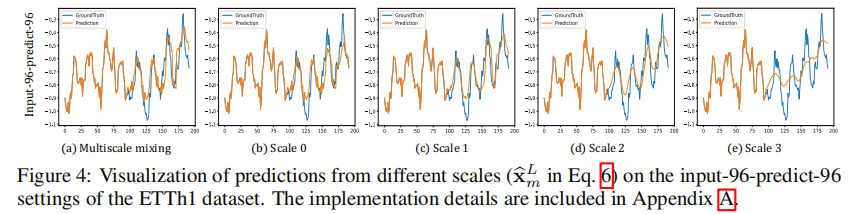
不同尺度趋势可视化
在本文的附录部分,提供了更为详尽的实验内容供读者参考。对于这些实验的深入分析和讨论,感兴趣的读者可以进一步查阅原文以获取完整的信息和细节。。
结论
TimeMixer模型的主要贡献和特点可以总结如下:
- 多尺度混合架构:TimeMixer采用了创新的多尺度混合架构,有效处理时间序列数据在不同时间尺度上的变化。
- 解耦过去信息:通过Past-Decomposable-Mixing(PDM)模块,模型能够解耦时间序列的过去信息,提取季节性和趋势性特征。
- 互补预测能力:利用FutureMultipredictor-Mixing(FMM)模块,TimeMixer集成了多个预测器,以利用多尺度观测数据的互补性,提高预测精度。
- 高效的运行时间:得益于全MLP(多层感知机)基础架构,TimeMixer在运行时表现出了良好的效率,适合实时或近实时预测场景。
dictor-Mixing(FMM)模块,TimeMixer集成了多个预测器,以利用多尺度观测数据的互补性,提高预测精度。
4. 高效的运行时间:得益于全MLP(多层感知机)基础架构,TimeMixer在运行时表现出了良好的效率,适合实时或近实时预测场景。
在一系列长期和短期的预测任务中,TimeMixer均取得了一致的先进性能,证明了其在时间序列预测领域的有效性。
🌟【紧跟前沿】“时空探索之旅”与你一起探索时空奥秘!🚀
欢迎大家关注时空探索之旅