备战2024年蓝桥杯 -- 每日一题
Python大学A组

        试题一：数星星
        试题二：小朋友排队
        试题三：逆序对数量
        试题四：火柴排队

---

试题一：数星星

【题目描述】

        天空中有一些星星，这些星星都在不同的位置，每个星星有个坐标。如果一个星星的左下方（包含正左和正下）有 k 颗星星，就说这颗星星是 k 级的。

        

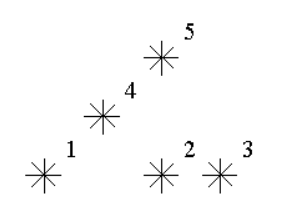
        例如，上图中星星 5 是 3 级的（1,2,4 在它左下），星星 2,4是 1 级的。例图中有 1 个 0 级，2 个 1 级，1 个 2 级，1 个 3 级的星星。给定星星的位置，输出各级星星的数目。

        换句话说，给定 N 个点，定义每个点的等级是在该点左下方（含正左、正下）的点的数目，试统计每个等级有多少个点。

【输入格式】

        第一行一个整数 N，表示星星的数目；

        接下来 N 行给出每颗星星的坐标，坐标用两个整数 x,y 表示；

        不会有星星重叠。星星按 y 坐标增序给出，y 坐标相同的按 x 坐标增序给出。

【输出格式】

        N 行，每行一个整数，分别是 0 级，1 级，2 级，……，N−1 级的星星的数目。

【数据范围】

        1≤N≤15000,
        0≤x,y≤32000

【输入样例】

5
1 1
5 1
7 1
3 3
5 5

【输出样例】

1
2
1
1
0

【解题思路】

        输入数据是按y值从小到大排序的，这个星星是第几级的计算方法就是前面有多少个x值比它小的。因为x不是小到大的输入，所以查询后得就得更新答案。

【Python程序代码】

n = int(input())
N = 52000
res = [0]*(N)
ans = [0]*(n+10)
def lowbit(x):return x&-x
def add(x,k):while x<=N:res[x]+=kx+=lowbit(x)
def quary(x):ans1 = 0while x:ans1 += res[x]x-=lowbit(x)return ans1
for i in range(n):x,y = map(int,input().split())x+=1ans[quary(x)] += 1add(x, 1)
for i in range(n):print(ans[i])

---

试题二：小朋友排队

【题目描述】

        n 个小朋友站成一排。现在要把他们按身高从低到高的顺序排列，但是每次只能交换位置相邻的两个小朋友。每个小朋友都有一个不高兴的程度。开始的时候，所有小朋友的不高兴程度都是 00。如果某个小朋友第一次被要求交换，则他的不高兴程度增加 1，如果第二次要求他交换，则他的不高兴程度增加 2（即不高兴程度为 3），依次类推。当要求某个小朋友第 k 次交换时，他的不高兴程度增加 k。请问，要让所有小朋友按从低到高排队，他们的不高兴程度之和最小是多少。如果有两个小朋友身高一样，则他们谁站在谁前面是没有关系的。

【输入格式】

        输入的第一行包含一个整数 n，表示小朋友的个数。

        第二行包含 n 个整数 H1,H2,…,Hn分别表示每个小朋友的身高。

【输出格式】

        输出一行，包含一个整数，表示小朋友的不高兴程度和的最小值。

【数据范围】

        1≤n≤100000,
        0≤Hi≤1000000

【输入样例】

3
3 2 1

【输出样例】

9

【解题思路】

        就是求每个小朋友与前面和后面的朋友构成的逆序对数量。

【Python程序代码】

n = int(input())
a = list(map(int,input().split()))
b = [0]*(n+10)
N = 2000000
s = [0]*N
def lowbit(x):return x&-x
def add(x,k):while x<=N:s[x]+=kx+=lowbit(x)
def quary(x):tep1 = 0while x:tep1 += s[x]x -= lowbit(x)return tep1
for i in range(n):a[i]+=1add(a[i],1)b[i+1] += i+1 - quary(a[i])
s = [0]*N
for i in range(n-1,-1,-1):add(a[i],1)b[i+1] +=quary(a[i]-1)
res = 0
for i in range(1,n+1):res += (b[i]+1)*b[i]//2
print(res)

---

试题三： 逆序对数量

【题目描述】

        给定一个长度为 n 的整数数列，请你计算数列中的逆序对的数量。逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i<j且 a[i]>a[j]，则其为一个逆序对；否则不是。

【输入格式】

        第一行包含整数 n，表示数列的长度。

        第二行包含 n 个整数，表示整个数列。

【输出格式】

        输出一个整数，表示逆序对的个数。

【数据范围】

        1≤n≤100000，
        数列中的元素的取值范围 [1,109]。

【输入样例】

6
2 3 4 5 6 1

【输出样例】

5

【解题思路】

        先离散化处理一下，模板题

【Python程序代码】

from bisect import *
n = int(input())
a = list(map(int, input().split()))
N = 200000
s = [0]*(N+10)
def lisan(a):b = sorted(list(set(a)))for i in range(len(a)):a[i] = bisect_left(b,a[i])+1return a
a = lisan(a)
def lowbit(x):return x&-x
def add(x,k):while x<=N:s[x]+=kx+=lowbit(x)
def quary(x):res = 0while x:res += s[x]x-=lowbit(x)return res
ans = 0
for i in range(n):ans += i - quary(a[i])add(a[i],1)
print(ans)

---

试题四：火柴排队

【题目描述】

        涵涵有两盒火柴，每盒装有 n 根火柴，每根火柴都有一个高度。 现在将每盒中的火柴各自排成一列， 同一列火柴的高度互不相同， 两列火柴之间的距离定义为：∑(ai​−bi​)2。其中ai​ 表示第一列火柴中第 i 个火柴的高度，bi​ 表示第二列火柴中第 i 个火柴的高度。每列火柴中相邻两根火柴的位置都可以交换，请你通过交换使得两列火柴之间的距离最小。请问得到这个最小的距离，最少需要交换多少次？如果这个数字太大，请输出这个最小交换次数对 10⁸−3 取模的结果。

【输入格式】

        共三行，第一行包含一个整数 n，表示每盒中火柴的数目。

        第二行有 n 个整数，每两个整数之间用一个空格隔开，表示第一列火柴的高度。

        第三行有 n 个整数，每两个整数之间用一个空格隔开，表示第二列火柴的高度。

【输出格式】

        一个整数，表示最少交换次数对 10⁸−3取模的结果。

【输入样例】

4
2 3 1 4
3 2 1 4

【输出样例】

1

【解题思路】

        顺序积之和>=乱序积之和>=逆序积之和，也就是把a和b数组都交换成大对应大，即大小等次是一样的。最少交换次数可以转化成，求一个映射数组的逆序对数量，先改造一下a,b数组，数组内容变成[值，索引]，然后将a和b按值大小进行排序，映射数组为c[a.idx]=b.idx。然后用树状数组求逆序对。

【Python程序代码】

n = int(input())
a = list(map(int, input().split()))
b = list(map(int, input().split()))
na,nb = [],[]
for i in range(n):na.append([a[i],i+1])nb.append([b[i],i+1])
na.sort(); nb.sort()
p,N = 10**8-3,10**5+10
c,tr = [0]*(N+10),[0]*(N+10)
for i in range(n):c[na[i][1]]=nb[i][1]
def lowbit(x):return x&-x
def add(x,k):while x<=N:tr[x] = (tr[x]+k)%px+=lowbit(x)
def quary(x):res = 0while x:res = (res + tr[x])%px-=lowbit(x)return res
ans = 0
for i in range(n,0,-1):ans = (ans + quary(c[i]-1))%padd(c[i],1)
print(ans)