目录
编辑
1.二叉树的链式存储
2.二叉树链式结构的实现
2.1树的创建
2.2二叉树的再理解
3.链式结构二叉树的遍历
3.1前序遍历实现:
编辑
3.2中序遍历实现
3.3后序遍历
编辑
4.链式二叉树节点数目的计算
4.1 总节点个数的计算
错误代码1:
错误代码2:
最优解:递归子问题划分解
4.2叶子节点个数的计算
4.3第k层节点个数的计算
5.二叉树查找节点值为x的节点
错误代码1:
正确代码:
6、二叉树的层序遍历
6.1利用层序遍历判断树是否为完全二叉树
7.二叉树的创建
8.二叉树的销毁
1.二叉树的链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是 链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所 在的链结点的存储地址 。链式结构又分为二叉链和三叉链。
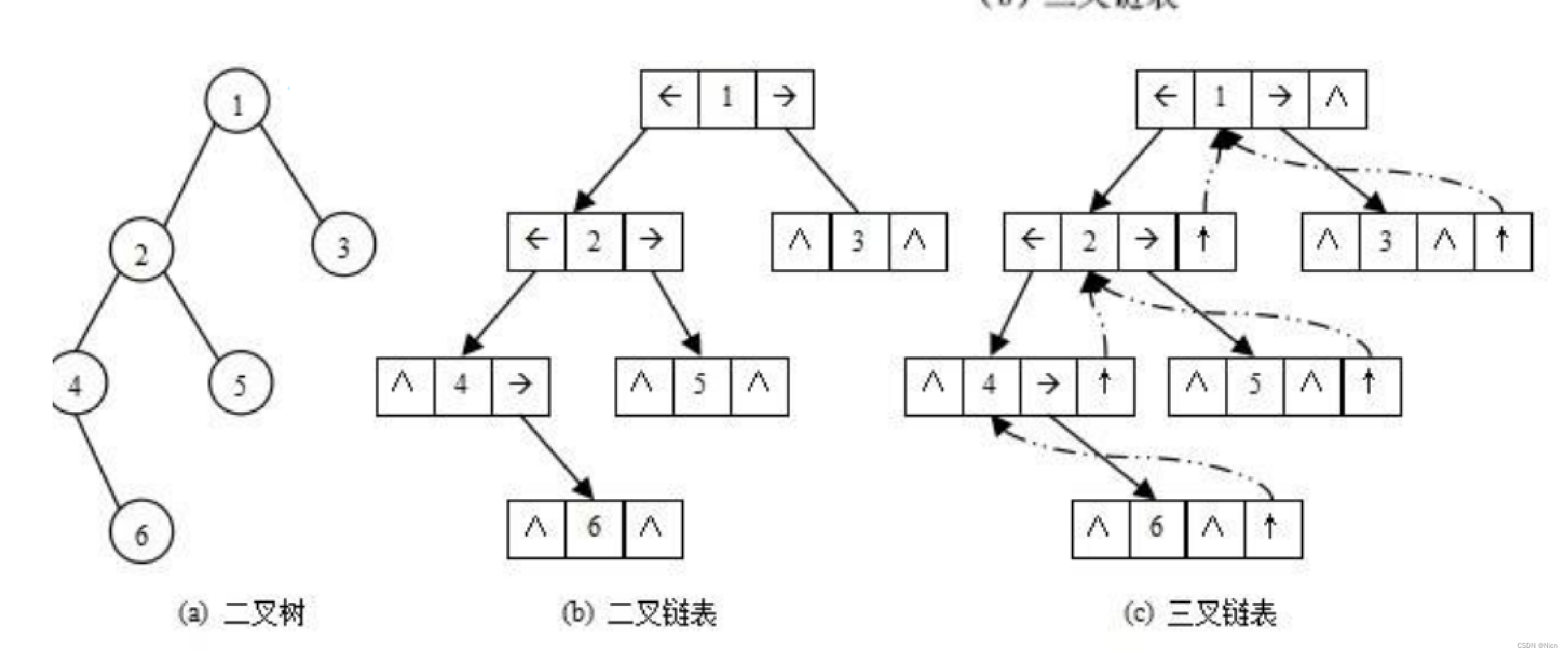
2.二叉树链式结构的实现
2.1树的创建
手动快速创建一棵简单的二叉树
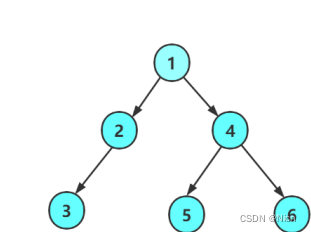
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->_left = node2;node1->_right = node4;node2->_left = node3;node4->_left = node5;node4->_right = node6;return node1;
}注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后序详解重点讲解
2.2二叉树的再理解
二叉树是: 1. 空树 2. 非空:根节点,根节点的左子树、根节点的右子树组成的。
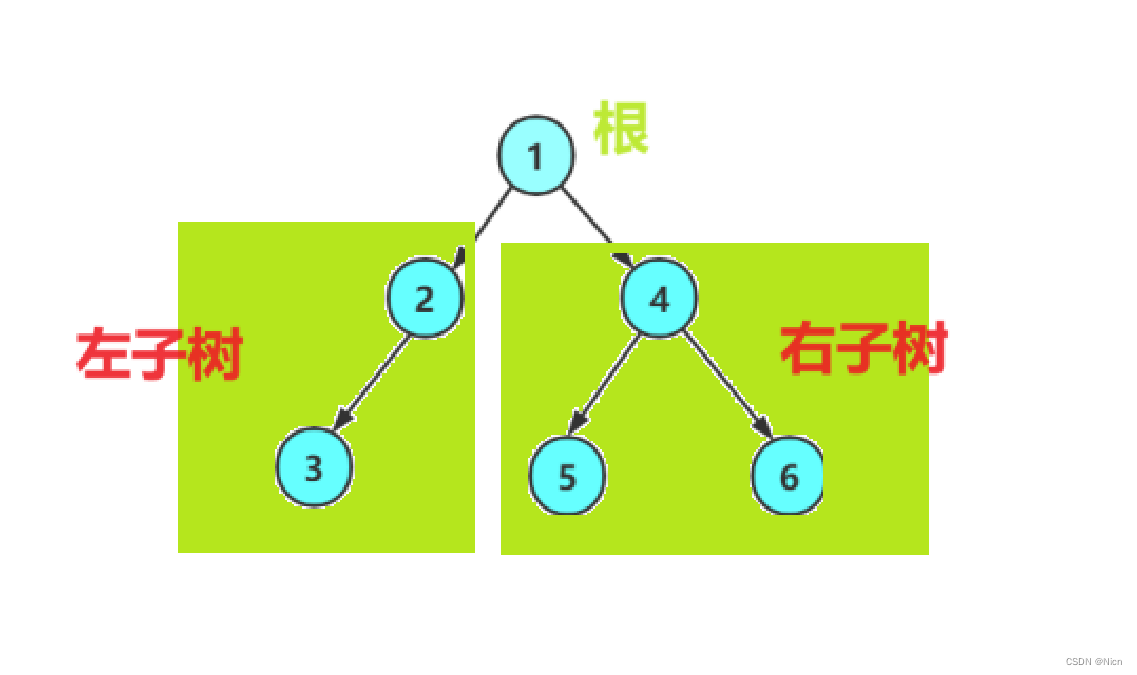
3.链式结构二叉树的遍历
二叉树的遍历
二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉 树中的节点进行相应的操作,并且每个节点只操作一次。
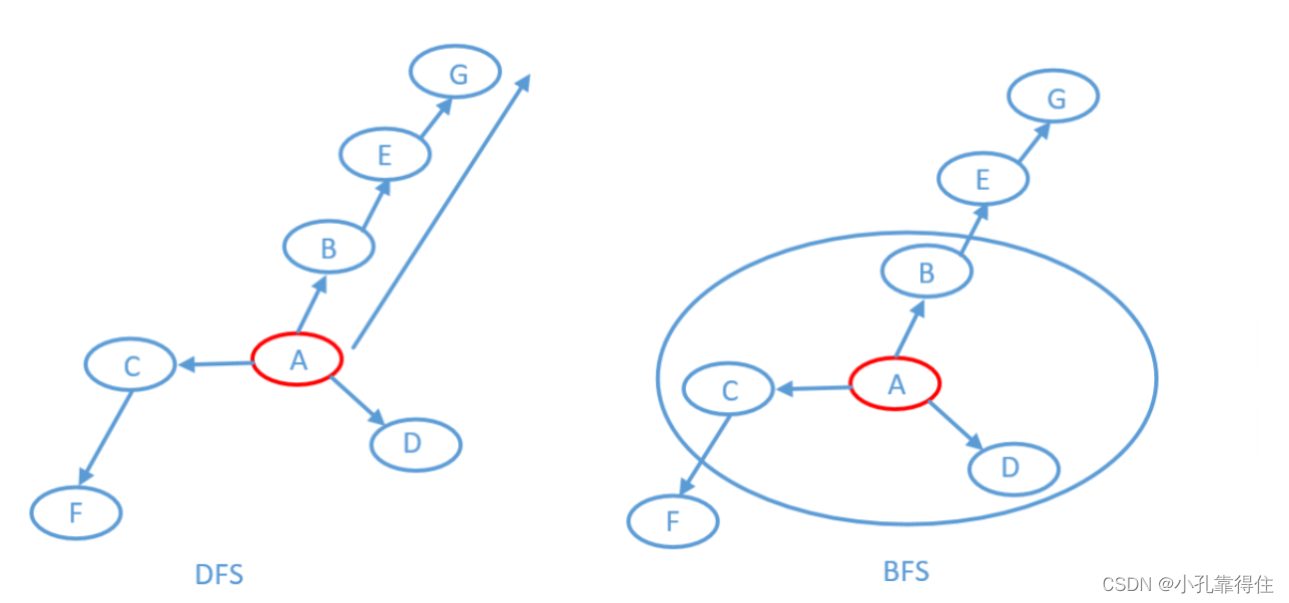
二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。根--左子树-右子树
- 2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。左子树--根--右子树
- 3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。左子树---右子树--根
3.1前序遍历实现:
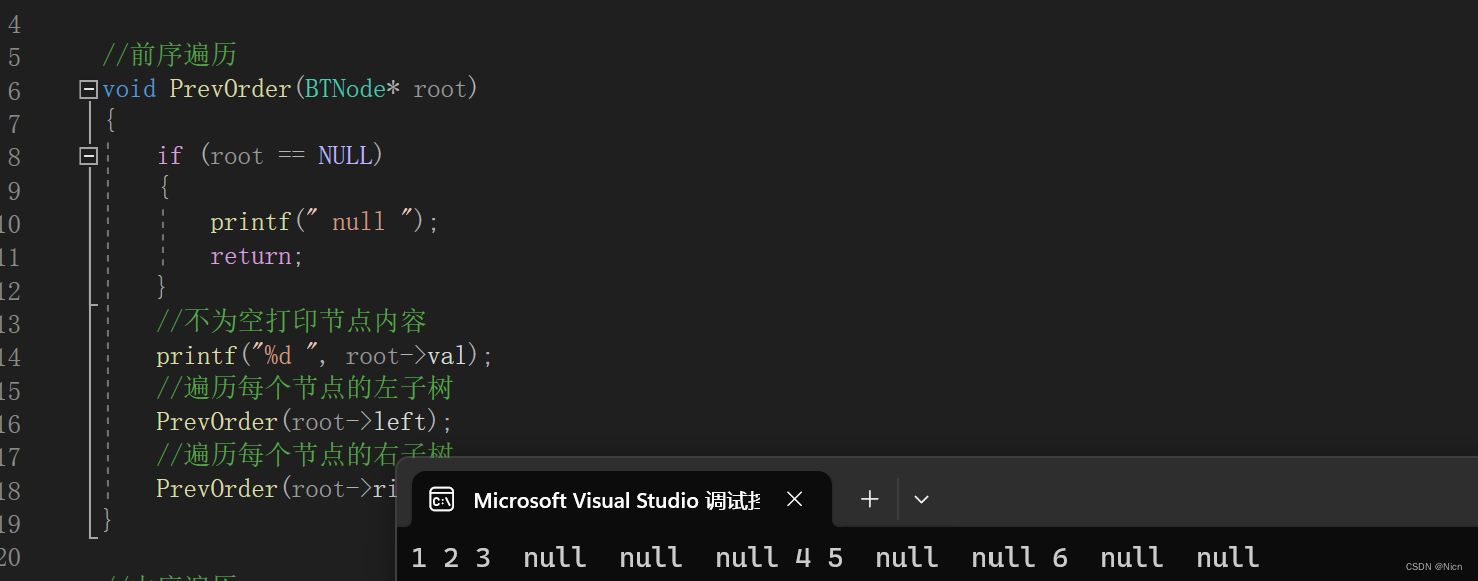
//前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){printf(" null ");return;}//不为空打印节点内容printf("%d ", root->val);//遍历每个节点的左子树PrevOrder(root->left);//遍历每个节点的右子树PrevOrder(root->right);
}递归展开图为:
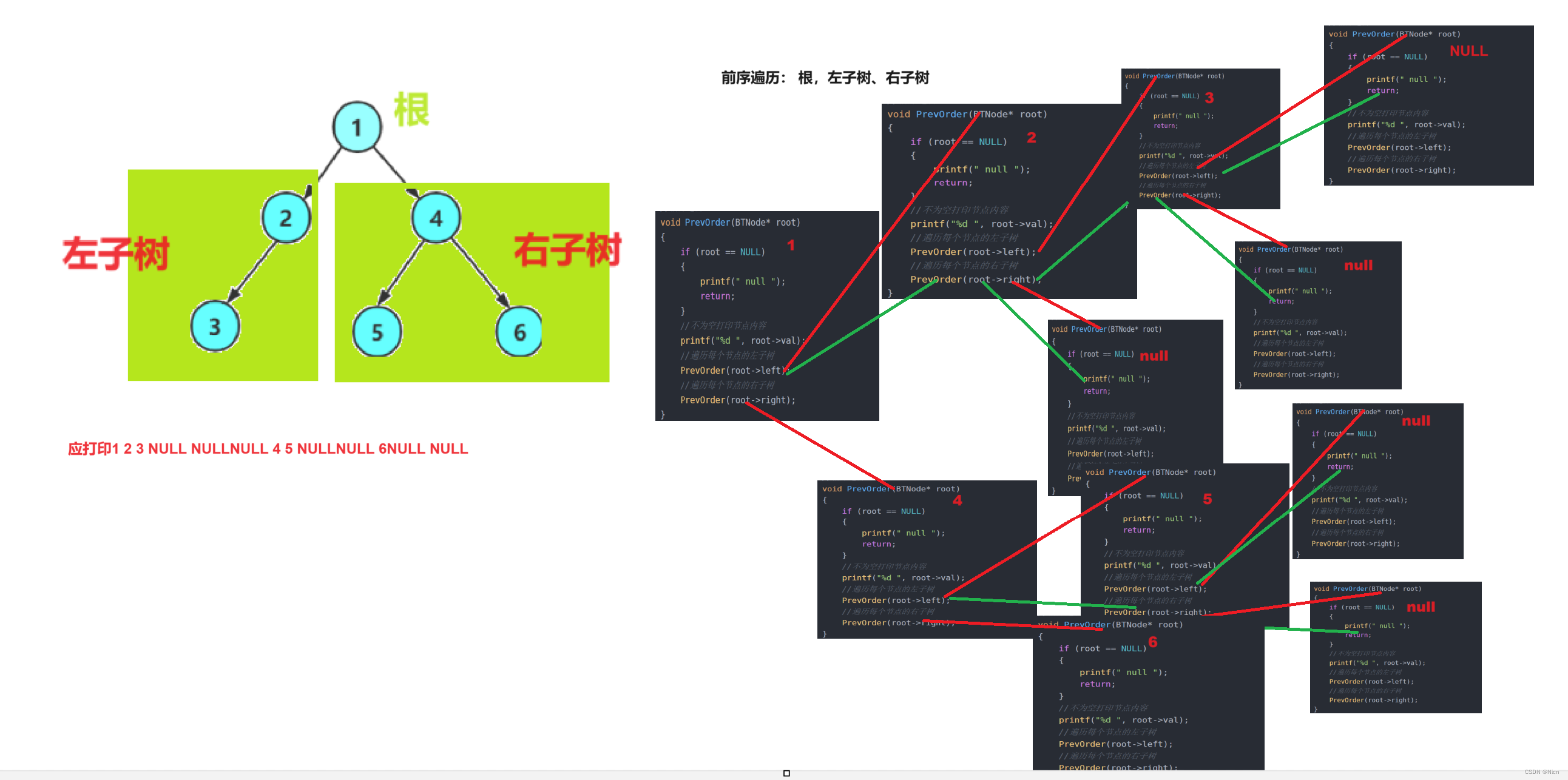
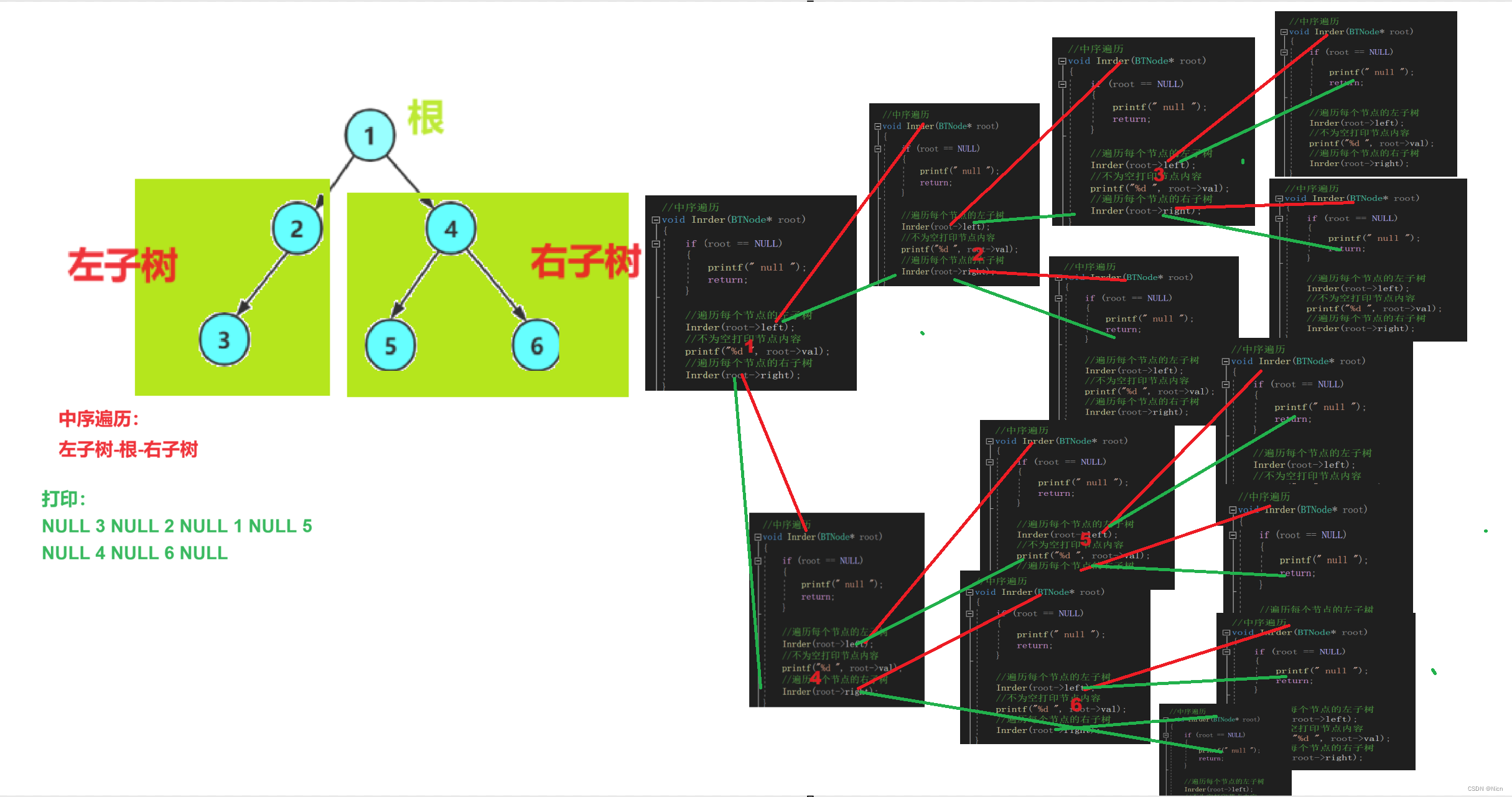
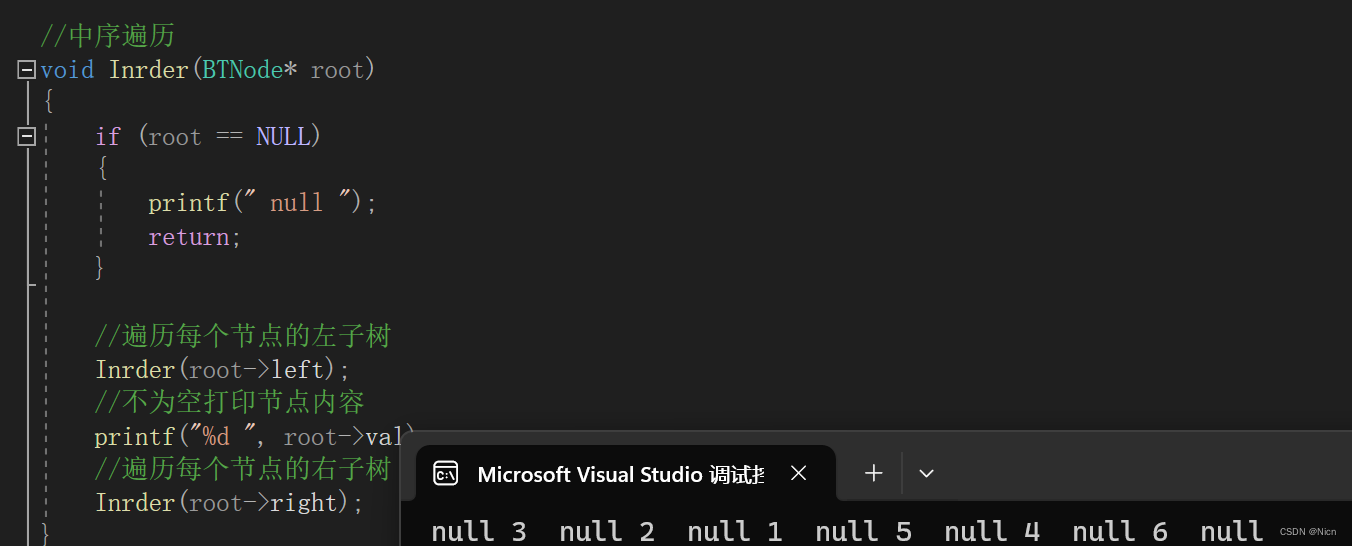
3.2中序遍历实现
//中序遍历 void Inrder(BTNode* root) {if (root == NULL){printf(" null ");return;}//遍历每个节点的左子树Inrder(root->left);//不为空打印节点内容printf("%d ", root->val);//遍历每个节点的右子树Inrder(root->right); }递归展开图为:
3.3后序遍历
void EndOrder(BTNode* root)
{if (root == NULL){printf(" null ");return;}//遍历每个节点的左子树EndOrder(root->left);//遍历每个节点的右子树EndOrder(root->right);//不为空打印节点内容printf("%d ", root->val);}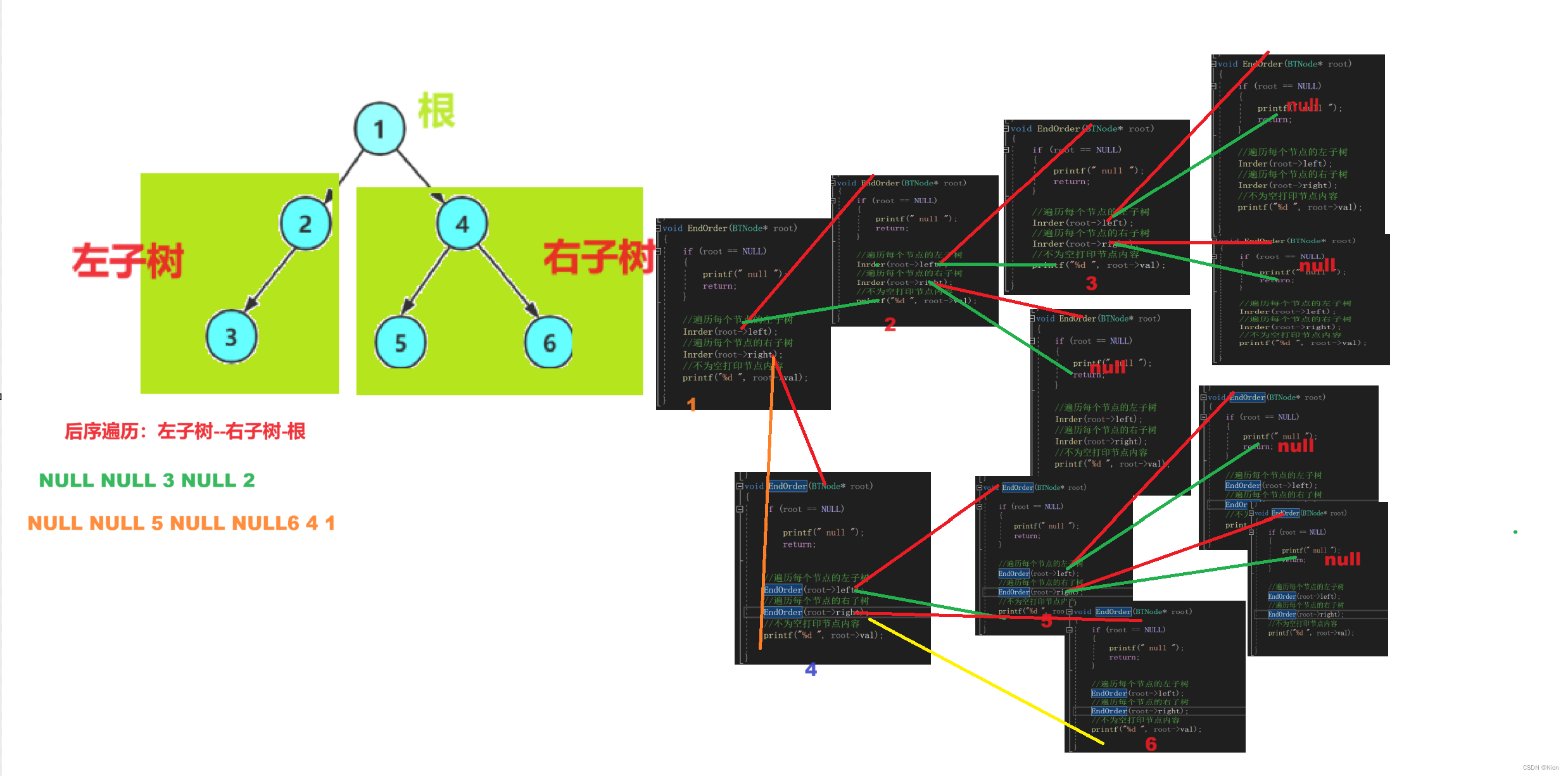
4.链式二叉树节点数目的计算
4.1 总节点个数的计算
简单思想:遍历一遍
错误代码1:
int TreeSize(BTNode* root)
{int size = 0;//记录树节点的个数if (root == NULL){return 0;}else{size++;//节点不为空,size+1}TreeSize(root->left);TreeSize(root->right);return size;}错误原因:每次调用函数,都会重新定义一个size,且赋值为0,当函数调用结束,变量销毁,size并没有带回调用这个函数的函数,最后输出的size为:1
错误代码2:
对上一个代码改进,将局部变量定义为全局变量:
局部的静态全局变量只会被执行一次
}//求二叉树的节点个数
int TreeSize(BTNode* root)
{static int size = 0;//记录树节点的个数if (root == NULL){return 0;}else{size++;//节点不为空,size+1}TreeSize(root->left);TreeSize(root->right);return size;} 
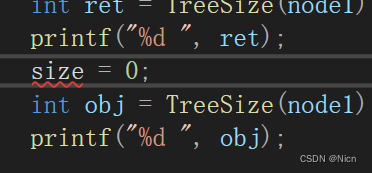
执行结果没有问题,但是当我们第二次调用这个函数或者再次计算其他树的节点个数的时候:
看到了明显的错误。第二次调用没有进行初始化,不符合用户的预期,因为static修饰的变的生命周期是全局,但是作用域没有扩张,不能手动修改。
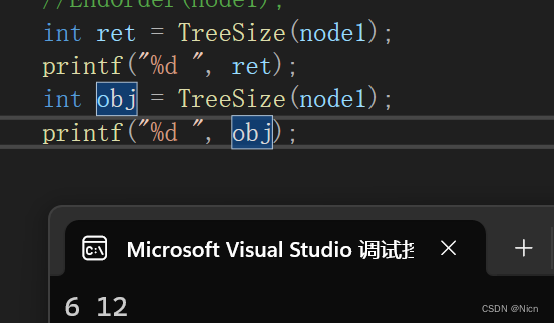
修改方式为将size定义为全局变量,然后手动每次调用前都初始化一下size:
int size = 0;//记录树节点的个数 int TreeSize(BTNode* root) {if (root == NULL){return 0;}else{size++;//节点不为空,size+1}TreeSize(root->left);TreeSize(root->right);return size;}int ret = TreeSize(node1); printf("%d ", ret); size = 0; int obj = TreeSize(node1); printf("%d ", obj);
最优解:递归子问题划分解
原理图解:
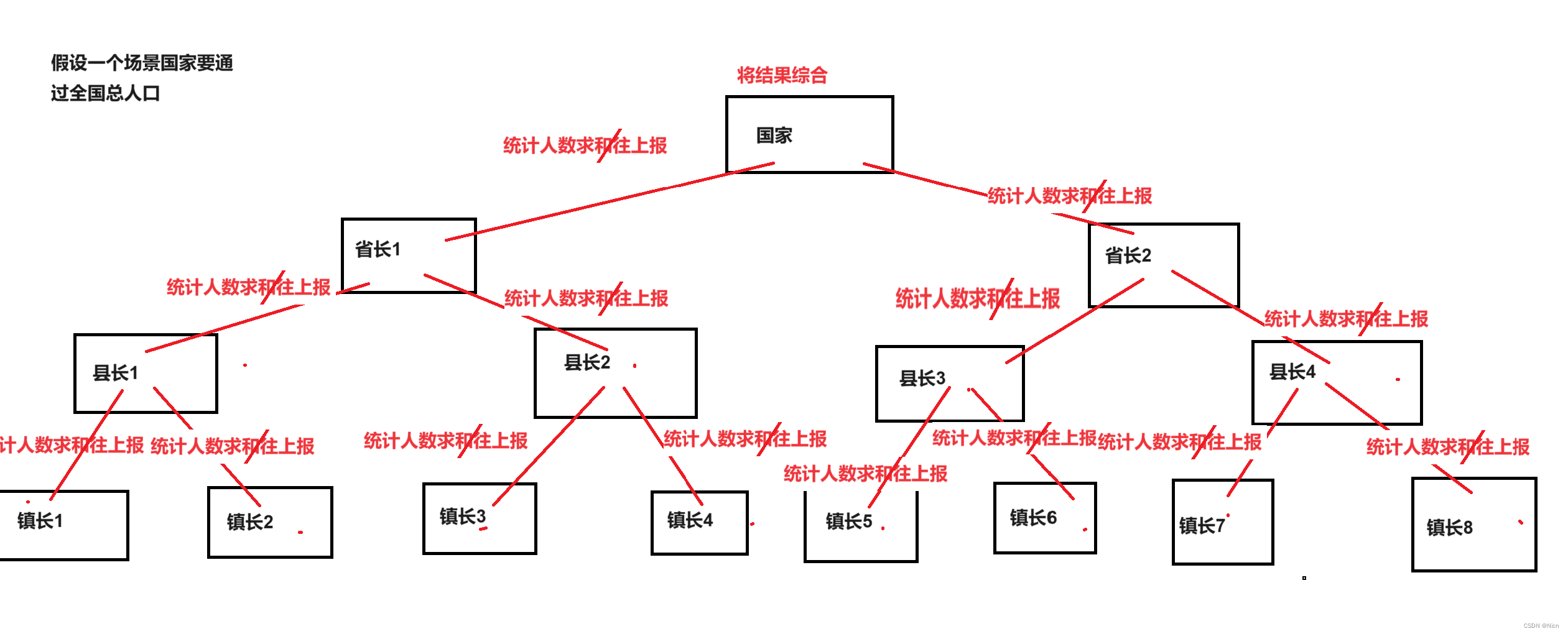
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;如果节点为空就返回0,如果不为空就返回左子树节点个数+右子树几点个数+自身
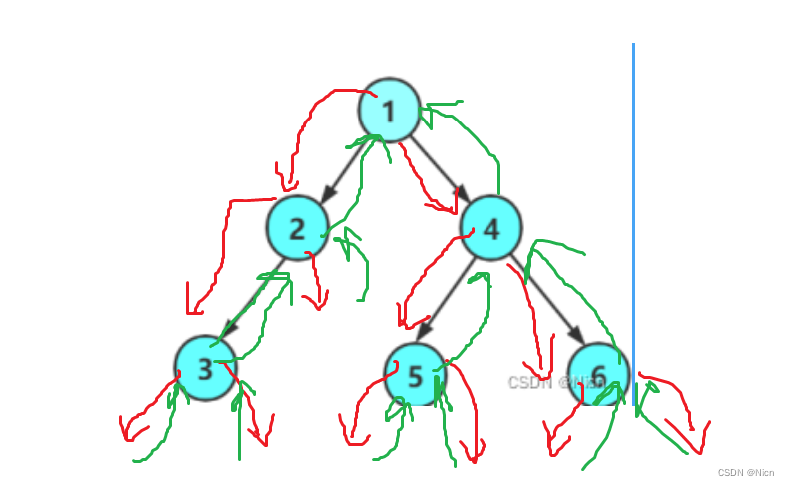
执行过程如图:红色代表向下执行,绿色代表返回:
4.2叶子节点个数的计算
思想:是空节点就返回0,是叶子节点就返回1,不是叶子节点就返回左子树的叶子节点数+右子树的叶子节点数。
叶子节点的特征:左子树与右子树为空
//叶子节点个数
int TreeLeaSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL)//叶子节点{return 1;}//不是空也不是叶子节点:return TreeLeaSize(root->left) + TreeLeaSize(root->right);}
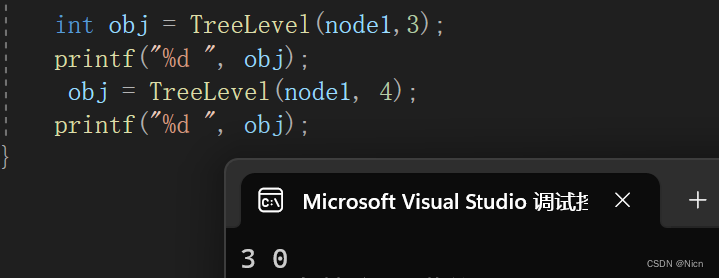
4.3第k层节点个数的计算
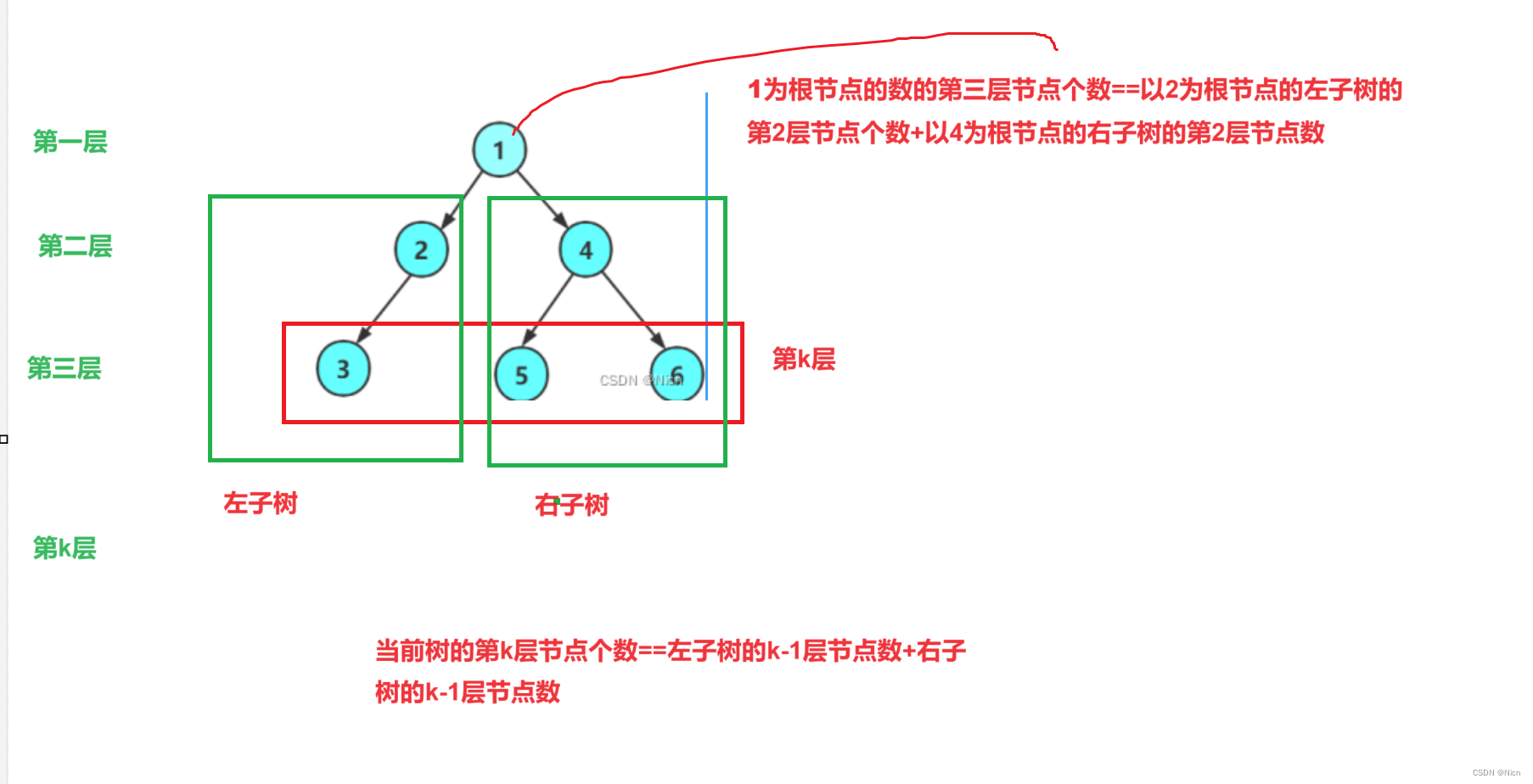

当层数减少到1,就返回这层节点的个数,每个节点都返回1,如果要求的k层没有节点就返回空
//第K层节点的个数
int TreeLevel(BTNode* root, int k)
{assert(k > 0);//层数都是正的,防止用户传错if (root == NULL){return 0;//树不存在或者遍历到空节点}if (k == 1){return 1;//递归到要求的那一层了}return TreeLevel(root->left, k - 1) + TreeLevel(root->right, k - 1);}
5.二叉树查找节点值为x的节点
推荐使用前序遍历效率高,后序遍历要最后才找根,根就遍历来两次,效率低了一层。
思路:如果根是就返回,如果不是就到左右子树中去找。
错误代码1:
BTNode* TreeFind(BTNode* root, int x)
{if (root == NULL){return NULL;}if (root->val = x){return root;}TreeFind(root->left, x);TreeFind(root->right, x);问题:到左右子树中去寻找过后,加入找到返回调用这个函数的函数中没有接收这个返回值的东西。
正确代码:
BTNode* TreeFind(BTNode* root, int x)
{if (root == NULL){return NULL;}if (root->val = x){return root;}BTNode* ret = NULL;ret = TreeFind(root->left, x);if (ret){return ret;}ret = TreeFind(root->right, x);if (ret){return ret;}return NULL;//左右都没有找到}6、二叉树的层序遍历
使用队列的思想,将树的根节点先入队列,将后面所有节点带出。
void LevelOrder(BTNode* root)
{Queue q;QUeueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);//取队头数据printf("%d ", front->val);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}//删除头部元素QueuepPop(&q);}QueueDestory(&q);
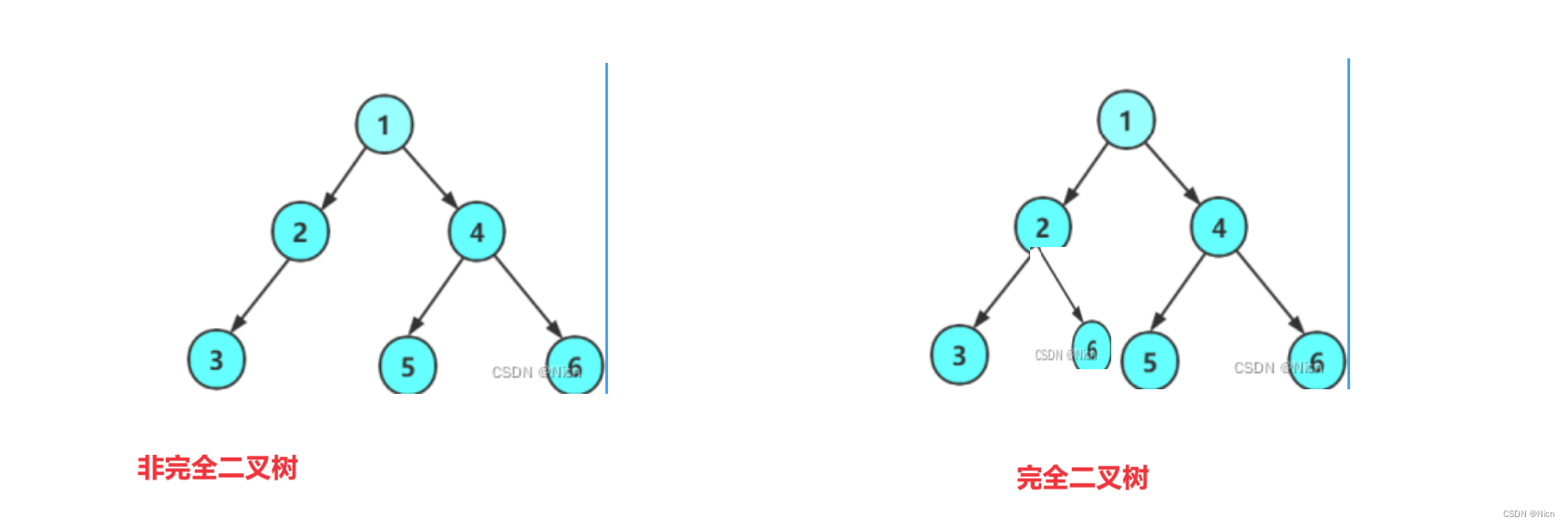
}6.1利用层序遍历判断树是否为完全二叉树
层序遍历:非空节点连续就是完全二叉树,非空节点不连续,非空节点中间有节点就不是完全二叉树
void LevelOrder(BTNode* root)
{Queue q;QUeueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);//取队头数据printf("%d ", front->val);if (front == NULL){break;//遇到空节点,跳出这层循环}QueuePush(&q, front->left);QueuePush(&q, front->right);//删除头部元素QueuepPop(&q);}//已经遇到空节点,如果队列后面的节点还有非空就不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);//取队头数据QueuepPop(&q);if (front != NULL){QueueDestory(&q);return false;}}QueueDestory(&q);return false;
}
7.二叉树的创建
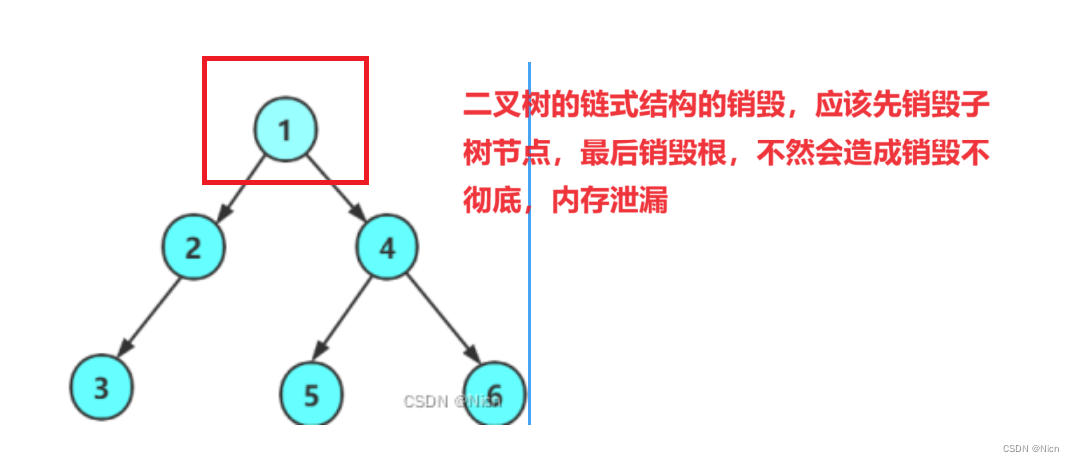
8.二叉树的销毁
由于每个节点都是在堆上malloc出来的,所以用完就销毁,返还给操作系统。
void TreeDestory(BTNode* root)
{if (root == NULL){return;}TreeDestory(root->left);TreeDestory(root->right);free(root);//root == NULL;这里不用置空,这里的root只是实参的零时拷贝//可以通过传入二级指针的方式来指针也可以在主函数置空}
9.结语
以上就是本期的所有内容,知识含量蛮多,大家可以配合解释和原码运行理解。创作不易,大家如果觉得还可以的话,欢迎大家三连,有问题的地方欢迎大家指正,一起交流学习,一起成长,我是Nicn,正在c++方向前行的奋斗者,数据结构内容持续更新中,感谢大家的关注与喜欢。