C语言（结构体，联合体，枚举的讲解）

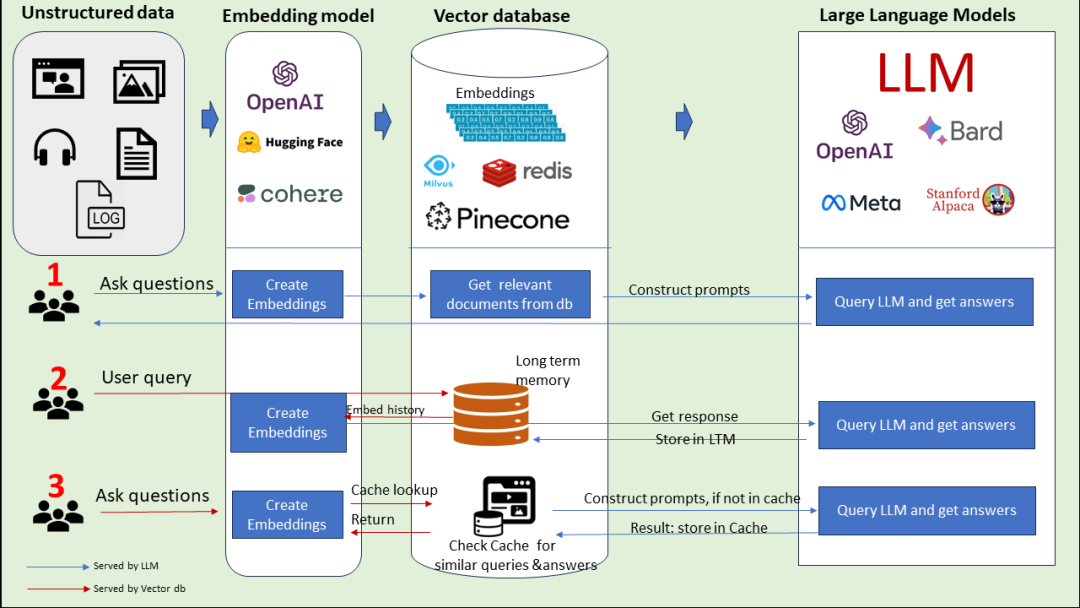
这期我们来讲解结构体，联合体，以及枚举的讲解，首先我们从概念开始一步一步的了解。

1，结构体

1.1概念

C 语言中的结构体是一种用户自定义的数据类型，它允许你将不同类型的变量组合在一起，从而形成一个新的数据类型。结构体在 C 语言中非常有用，可以用于表示复杂的数据结构，比如学生信息、员工记录、图形对象等。

定义结构体的基本语法如下：c
struct 结构体名 {数据类型 成员1;数据类型 成员2;// 更多成员...
};
在这里，struct 是关键字，后面跟着的是结构体的名称，
紧接着是由大括号括起来的成员列表。
每个成员都有其自己的数据类型，可以是基本类型（如整型、浮点型、字符型等），
也可以是其他的结构体类型。

1.2代码实现

很简单吧，我们先来试一下

1.3结构体内存对齐

什么是内存存对齐，为什么结构体会存在内存对齐，内存对齐的规则是什么，，反正也不会告诉你。

在 C 语言中，结构体内存对齐是指编译器在分配内存时，为了提高访问效率而进行的一种内存布局优化。结构体的内存对齐是由编译器来决定的，它遵循特定的对齐规则，以确保结构体成员的访问具有最佳的性能。

在大多数情况下，编译器会根据平台的要求和 CPU 架构的特性来进行内存对齐。常见的内存对齐规则如下：

1.成员变量的偏移量必须是其大小的整数倍。

2.结构体的大小必须是其最大成员大小的整数倍。

根据内存对齐规则，编译器会进行内存对齐，可能导致结构体的大小不等于其成员变量大小之和。这是因为编译器会在适当的位置插入填充字节，以确保结构体成员按照对齐要求排列，从而提高访问效率。

具体的对齐规则可能会因编译器和平台而异，你可以使用 sizeof 运算符来获取结构体的大小，以便更好地理解编译器对结构体内存布局所做的优化。

当然我们也可以通过设置偏移量来改变其大小

2，联合体

2.1概念

在 C 语言中，联合体（union）是一种特殊的数据结构，它允许在同一个内存位置存储不同类型的数据。与结构体不同的是，联合体中的各个成员共享同一块内存空间，因此联合体的大小由最大的成员决定。

2.2代码实现

3，枚举

3.1概念

在 C 语言中，枚举（enum）是一种用户定义的数据类型，用于定义一组具名的整型常量。枚举类型可以帮助提高代码的可读性，使程序员能够使用有意义的符号名称来表示特定的值。

3.2代码实现

3.3define和枚举对比

很多初学C语言的小伙伴觉得枚举很鸡肋，用define就能实现的事情干嘛要用枚举。

枚举的优点：

类型安全性：枚举提供了类型安全，因为枚举常量属于特定的枚举类型，在赋值和比较时具有类型信息。
可读性：枚举符号名可以使代码更加易读和清晰，因为它们提供了有意义的名称来表示常量值。
编译时检查：由于枚举常量在编译时被解析，因此编译器可以对其进行检查，避免拼写错误或值的误用。

宏定义的优点：

灵活性：宏定义可以定义更复杂的常量，如带参数的宏、条件编译等，具有更大的灵活性。
无类型约束：宏定义不受类型限制，可以用于定义任何类型的常量，包括字符串、表达式等。

如何选择：

当需要一组相关的常量，并且这些常量属于同一逻辑实体时，通常使用枚举更为合适。
当需要定义简单的常量或进行代码替换时，宏定义可能更加适用。

总的来说，枚举提供了更好的可读性和类型安全性，而宏定义则更加灵活。

存在就有道理第

4，每期一问

上期答案：如何写出自己的atoi函数

#include<stdio.h>
#include<assert.h>
#include<ctype.h>
#include<stdlib.h>
enum State
{VAILD,INVAILD
}Sta = INVAILD;//创造变量默认为非法int my_atoi(const char* str)
{assert(str);if (*str == '\0'){return 0;}while (isspace(*str)){str++;}int flag = 1;if (*str == '+'){flag = 1;str++;}else if (*str == '-'){flag = -1;str++;}long long ret = 0;while (*str != '\0'){if (isdigit(*str)){ret = ret * 10 + flag * (*str - '0');//减去字符0，才是数字0if (ret > INT_MAX || ret < INT_MIN){return 0;}}else{return (int)ret;//强制类型转化为int（函数的返回值是int）}str++;}if (*str == '\0'){Sta = VAILD; //正常转换完了，到末尾的 \0}return (int)ret;