在上篇文章我们了解了平衡二叉树的优势，了解到平衡二叉树能够对不平衡的节点施加旋转，使得树达趋于平衡，以提升查询效率，操作效率很高，与之同时也存在着不少的问题，例如我们在实际使用中会通常会将树加载到内存中，如果节点少的话倒没有什么问题，但节点一多，例如上百万的节点，则高度很大，这时候进行一次IO操作就会出现性能问题。

        关于此问题我们详细展开，平衡二叉树每个节点只存储一个键值和数据的，每个磁盘块仅仅存储一个键值和数据。如果要存储海量的数据（如1000w），那构建平衡二叉树的时候耗时就会多，其平衡二叉树的节点也会非常的多，高度也会极其高，查找数据时会进行很多次的磁盘IO（高度=IO次数），效率将会极低。为了解决这个问题，接下来我们来讲解多叉树，其数据结构就是一种单个节点可以存储多个键值和数据的平衡树。

多叉树

        又称“多路查找树（muitl-way search tree） ”，每一个节点的子树可以多余两个，且每个节点处可以存储多个元素，常见的就是B树、B+树等。多叉树通过重新组织节点，降低了树的高度，显著提高了IO效率。

此处的B是Balanced的意思，不是Binary的意思

 

         操作系统IO操作都会利用磁盘预读原理，如果一个节点大小是一个存储页（4kb），存储每个节点只需要一次IO即可完成存储。B树在存储系统里面广泛被使用，例如数据库系统和文件系统等。

B树

        也叫 B-Tree，B-树，全称是 Balanced Tree，是一种多路平衡查找树。一个节点包括多个key (数量看业务)，具有M阶的B树，每个节点最多有M-1个Key。节点的key元素个数就是指这个节点能够存储几个数据。每个节点最多有m个子节点，最少有M/2个子节点，其中M>2。

每个节点拥有最多的子节点，子节点的个数一般称为阶。

阶：m阶是代表每个节点最多有m个分支（子树）

        数据集合分布在整个树里面，叶子节点和非叶子节点都存储数据；类似在整个树里面做一次二分查找。B 树相对于平衡二叉树，每个节点存储了更多的键值（key）和数据（data）。实际业务中B树的阶数一般大于100，存储大量数据，B树高度也会很低，查询效率会更高, 

树的度：这棵树里面节点最大的度，节点的度：当前节点有几个孩子

 如下图为例：M阶B树，M=3,每个节点最多有M-1个Key，每个节点最多有M个节点，树的度=3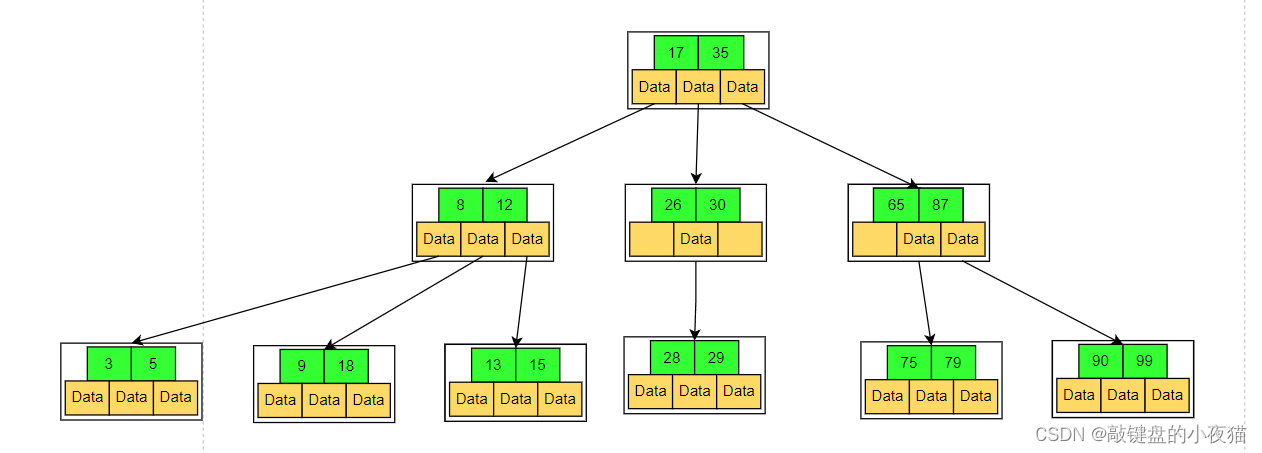

 动画效果演示：B-Tree Visualization

 应用场景

1）在数据库中，B树用来维护索引，用来提高查询效率，一个节点可以存储整个页（即磁盘块）；
2）在文件系统中，B树用来存储文件的目录信息，提高文件的访问效率；
3）在操作系统中，B树可以用来存储内存管理信息，提高内存的分配效率；

举一反三

        3层的B树，阶数为1024，最多容纳多少个元素？

答：B树的阶数表示每个结点最多可以有多少个子结点，因此B树的阶数为1024，表示每个结点最多可以有1024个子结点。由于B树的3层，因此根结点可以有1024个子结点，每个子结点又可以有1024个子结点，因此一个3层的B树，阶数为1024，B树的每一层的节点数都是阶数的幂次方。 

计算总容量：把每一层的节点数相加 即1024^1+1024^2+1024^3 大约是 11亿个节点，假如每个节点放一个元素就是11亿个，所以在10亿个数据中找目标值，常规小于3次磁盘IO即可找到目标值，比平衡二叉树的30次提升了不少，平衡二叉树的高度就等于每次查询数据时磁盘 IO 操作的次数。

10亿的数据量，log2(N)约等于30次磁盘IO，log2(N) 相当于2的多少次方（立方）等于N，例：log2 (8）= 3，2的30次方=1073741824，所以就是30次磁盘IO。