作者：CSDN @ _养乐多_

在神经网络领域，梯度下降是一种核心的优化算法，本文将介绍神经网络中梯度下降法更新参数的公式，并通过实例演示其在模型训练中的应用。通过本博客，读者将能够更好地理解深度学习中的优化算法和损失函数，为学习和应用深度学习打下坚实的基础。

---

---

一、概念

1.1 交叉熵损失函数

了解梯度下降方法更新参数之前，需要先了解交叉熵损失函数，可以参考《损失函数｜交叉熵损失函数》，讲的很详细。交叉熵可以理解为模型输出值和真实值之间的差异，交叉熵损失越小，表示模型预测结果与真实情况越接近，模型的精度也就越高。

梯度下降更新参数的过程其实就是在反向求导减小梯度的过程中找到差异最小时的模型参数。

1.2 梯度下降

在机器学习和深度学习中，经常需要通过调整模型的参数来使其在训练数据上表现得更好，而梯度下降是一种常用的方法。

梯度下降的基本思想是沿着目标函数的负梯度方向进行迭代，以找到函数的局部最小值。具体而言，对于一个多维函数，梯度下降通过计算目标函数在当前参数位置的梯度（即偏导数），然后按照梯度的反方向更新参数，使得函数值不断减小。这个过程重复进行，直到达到某个停止条件，比如达到了指定的迭代次数或者目标函数的变化小于某个阈值。

梯度下降的核心公式：

$${\theta }^{new}=\theta -\eta \frac{\partial LOSS}{\partial \theta }\text{\hspace{1em}(1)}$$

其中，${\theta }^{new}$表示新的权重，$\theta$表示旧的（初始/上一次迭代）权重，$\eta$ 是学习率（learning rate）。

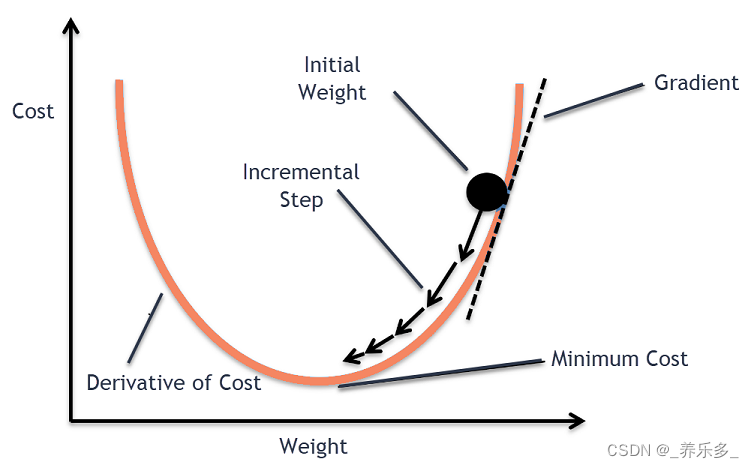
图片来自“Gradient Descent Algorithm: How does it Work in Machine Learning?”

梯度下降算法有多种变种，如批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）和小批量梯度下降（Mini-batch Gradient Descent）等，它们在计算梯度的方式和参数更新的规则上略有不同，但核心思想相似。

二、梯度下降更新模型参数

了解了交叉熵损失函数的概念之后，我们来看看梯度下降如何利用这个损失函数来更新模型参数。

这个过程是神经网络的核心，能看懂这个过程，也就基本懂深度神经网络了。

2.1 定义模型

首先，假设模型为下式，其中，$True$为模型的真实输出值，$\omega$和$b$是模型需要更新的参数，分别为权重和偏置。
$$True=\Sigma {\omega }_i\cdot x_i+b\text{\hspace{1em}(2)}$$

2.2 损失函数的定义

接下来，我们定义一个损失函数。在这个例子中，我们假设损失函数是交叉熵损失，因为这个函数简单且容易推导，但是$LOSS$函数使用均方差MSE（Mean Squared Error）的形式，这可能有些混淆。不管混淆不混淆吧，我们就用该函数来描述梯度下降更新参数的过程。

损失函数的定义：
$$LOSS=(真实输出值-期望输出值{)}^2\text{\hspace{1em}(3)}$$
$$LOSS=(True-Pred{)}^2\text{\hspace{1em}(4)}$$

其中，$True$ 是真实输出，$Pred$ 是模型预期输出。

$LOSS$对$True$求偏导，得

$$\frac{\partial LOSS}{\partial True}=2(True-Pred)\text{\hspace{1em}(5)}$$

2.3 对于权重$w_i$的更新

先对$w_i$求偏导，这里公式（6)是梯度下降方法的定式，得
$$w_i^{new}=w_i-\eta \frac{\partial LOSS}{\partial w_i}\text{\hspace{1em}(6)}$$
其中，$w_i^{new}$表示新的权重，$w_i$表示旧的（初始/上一次迭代）权重，$\eta$ 是学习率（learning rate）。

通过链式法则，$\frac{\partial LOSS}{\partial w_i}$可以表示为：
$$\frac{\partial LOSS}{\partial w_i}=\frac{\partial LOSS}{\partial True}\frac{\partial True}{\partial w_i}\text{\hspace{1em}(7)}$$
因为$True$是$\Sigma \omega \cdot x_i+b$计算得到的，所以：
$$\frac{\partial True}{\partial w_i}=x_i\text{\hspace{1em}(8)}$$
因此，权重 $w_i$的更新规则为：
$$w_i^{new}=w_i-\eta \cdot 2（True-Pred）\cdot x_i\text{\hspace{1em}(9)}$$

2.4 对于偏置$b$的更新

$$b^{new}=b-\eta \frac{\partial LOSS}{\partial b}\text{\hspace{1em}(10)}$$

其中，$b^{new}$表示新的偏置，$b$表示旧的（初始/上一次迭代）偏置，$\eta$ 是学习率（learning rate）。
同样的，通过链式法则，$\frac{\partial LOSS}{\partial b}$可以表示为：
$$\frac{\partial LOSS}{\partial b}=\frac{\partial LOSS}{\partial True}\frac{\partial True}{\partial b}\text{\hspace{1em}(11)}$$
因为$True$是$\Sigma \omega \cdot x_i+b$计算得到的，所以：

$$\frac{\partial True}{\partial b}=1\text{\hspace{1em}(12)}$$
因此，偏置$b$的更新规则为：
$$b^{new}=b-\eta \cdot 2(True-Pred)\text{\hspace{1em}(13)}$$

三、举例推导

3.1 样本数据

下表中，$X_1$和$X_2$分别为自变量，可以理解为特征变量，期望输出就是分类或者回归时用到的目标变量，可以理解为标签数据。

ID	$X_1$	$X_2$	期望输出
1	0.1	0.8	0.8
2	0.5	0.3	0.5
…	…	…	…

3.2 初始化模型

因为模型是 $True=\Sigma \omega \cdot x_i+b$ ，分别设置模型的初始参数：$\eta$为0.1，$w_1$为0，$w_2$为0，$b$为0。

3.3 第1次迭代

将样本1（$x_1$为0.1，$x_2$为0.8，期望输出为0.8）代入模型，经过$w_1\cdot x_1+w_2\cdot x_2+b$，得 $0✖0.1+0✖0.8+0$，最终输出值为0，然而期望输出值为0.8，根据损失函数$LOSS=(True-Pred{)}^2$,得$LOSS=(输出值-期望输出值{)}^2$，即$(0-0.8{)}^2$，那么$LOSS$为$0.64$。
根据公式(9)，$w_1^{new}=w_1-\eta \cdot 2(True-Pred)\cdot x_1$，先来更新$w_1$，得$0-0.1✖2✖(0-0.8)✖0.1$，最终得到新的权重$w_1$为0.016。
同样的更新$w_2$，$w_2^{new}=w_2-\eta \cdot 2(True-Pred)\cdot x_2$，得$0-0.1✖2✖(0-0.8)✖0.8$，得到新的权重$w_2$为0.128。
接着根据公式(13)，$b^{new}=b-\eta \cdot 2(True-Pred)$，更新偏置$b$，得$0-0.1✖2✖(0-0.8)$，得到新的偏置$b$为0.16。

3.4 第2次迭代

经过3.3节第1次迭代更新的参数，现在新的参数为：$\eta$为0.1，$w_1$为0.016，$w_2$为0.128，$b$为0.16。

接着基于这一组新的参数继续训练模型。

将样本2（$x_1$为0.5，$x_2$为0.3，期望输出为0.5）代入3.3节更新的模型中，经过$w_1\cdot x_1+w_2\cdot x_2+b$，得 $0.016✖0.5+0.128✖0.3+0.16$，最终输出值为0.2064，然而期望输出值为0.5，根据损失函数$LOSS=(True-Pred{)}^2$,得$LOSS=(输出值-期望输出值{)}^2$，即$(0.2065-0.5{)}^2$，那么$LOSS$为$0.0862$。
根据公式（9），$w_1^{new}=w_1-\eta \cdot 2(True-Pred)\cdot x_1$，先来更新$w_1$，得$0.1-0.1✖2✖(0.2064-0.5)✖0.1$，最终得到新的权重$w_1$为0.04536。
同样的更新$w_2$，$w_2^{new}=w_2-\eta \cdot 2(True-Pred)\cdot x_2$，得$0.128-0.1✖2✖(0.2064-0.5)✖0.3$，得到新的权重$w_2$为0.14562。
接着根据公式(13)，$b^{new}=b-\eta \cdot 2(True-Pred)$，更新偏置$b$，得$0.16-0.1✖2✖(0.2064-0.5)$，得到新的偏置$b$为0.21872。

3.5 第n次迭代

和前面的方式一样，用户设置迭代次数n，迭代n次结束以后就可以得到一组模型参数，作为本次训练的最终模型。以后只要有新的$X_1$，$X_2$输入，就会计算一个$输出Y$，这个过程就是模型应用（推理）。当然，并不是说迭代的次数越多，模型精度就越高，有可能会过拟合。

四、其他

模型精度也和学习率有关，学习率影响着模型在训练过程中收敛速度以及最终的收敛状态。

下图来自https://www.kdnuggets.com/2020/05/5-concepts-gradient-descent-cost-function.html。

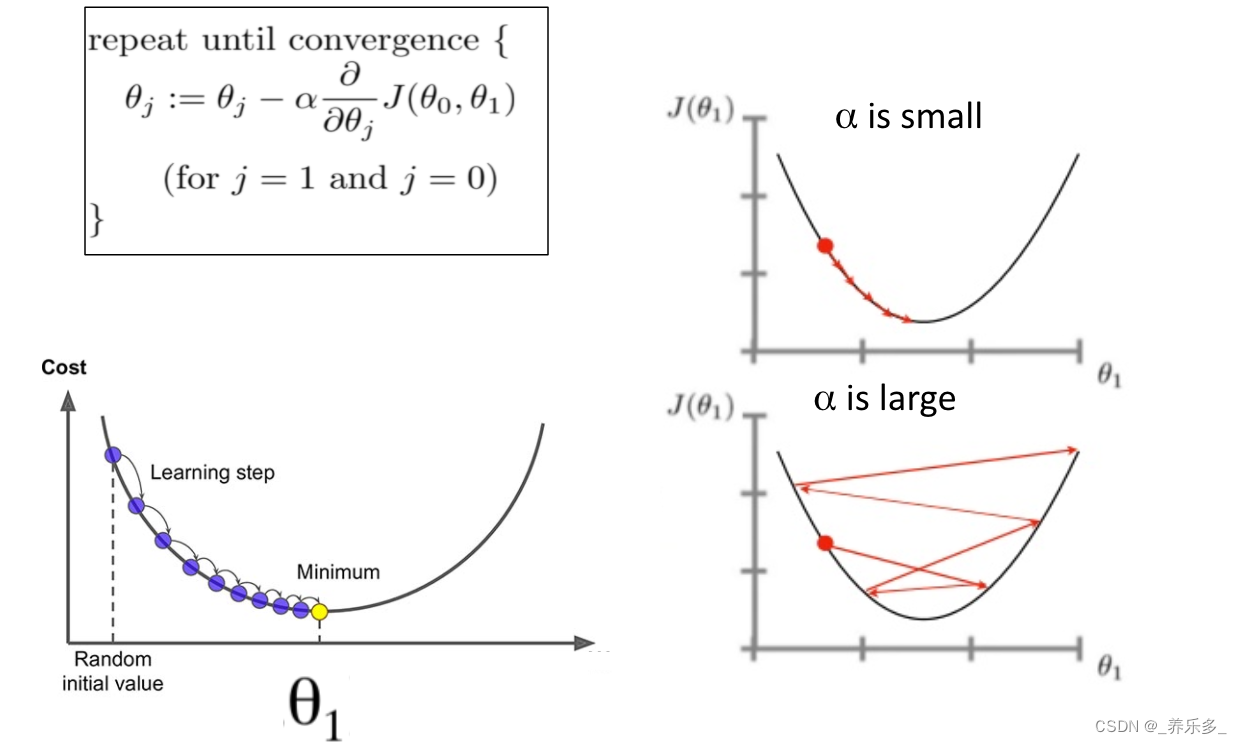
如上图右下图示所示，学习率过大可能导致参数在优化过程中发生震荡，甚至无法收敛；而学习率过小（上图右上图示）则可能导致收敛速度过慢，耗费大量的时间和计算资源。因此，需要在学习率和模型精度之间取一定的平衡。