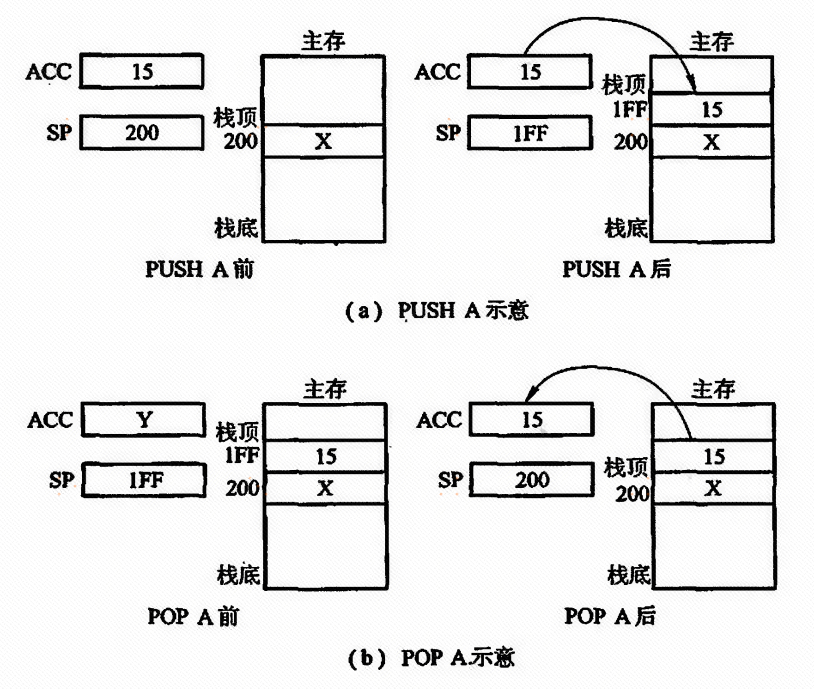
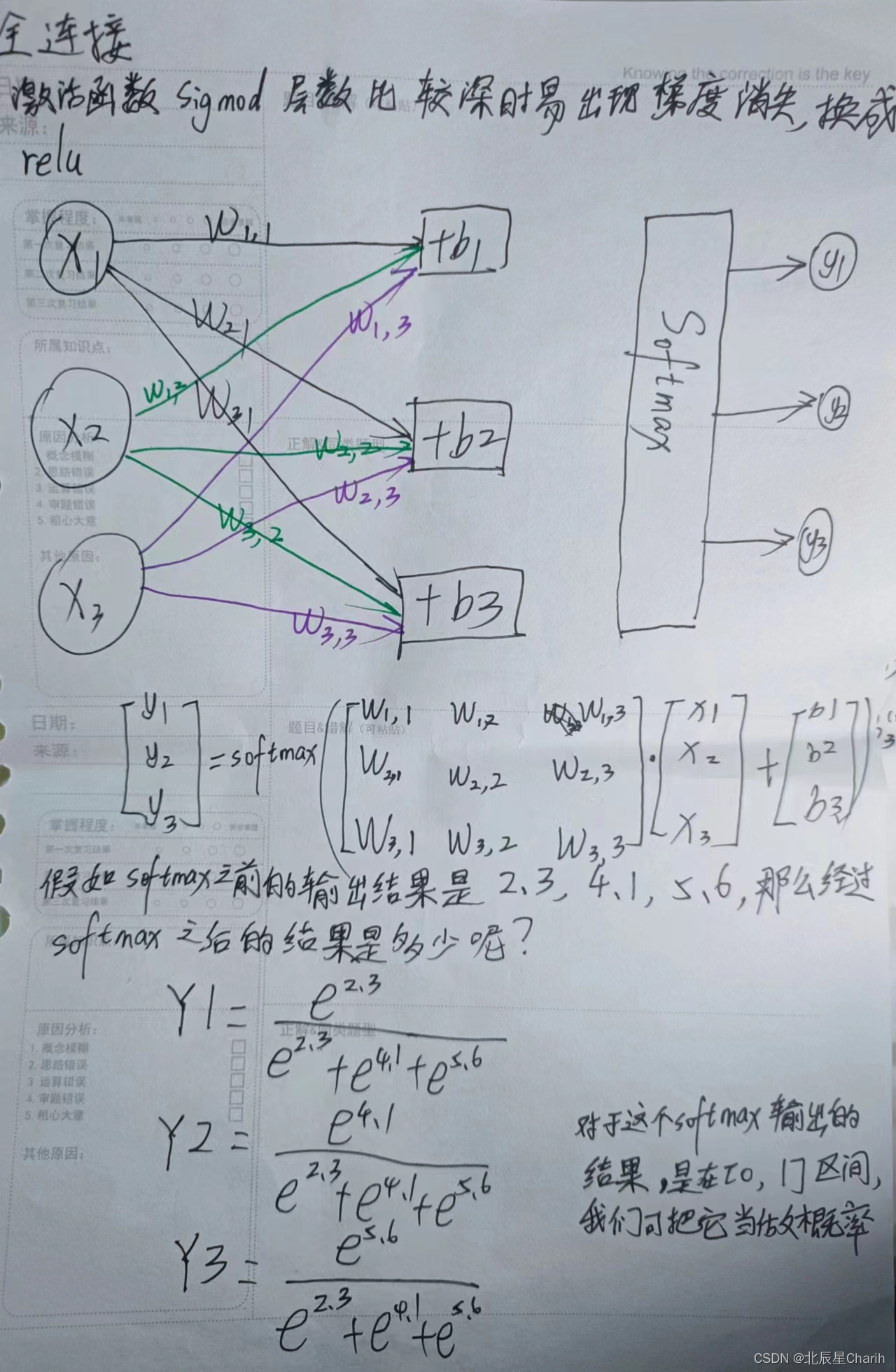
引言:
在计算机科学和算法领域中,快速幂算法是一种用于高效计算幂运算的技术。在实际编程中,特别是在处理大数幂运算时,快速幂算法能够显著提高计算效率。本文将介绍如何在Java中实现快速幂算法,并给出一些示例代码和应用场景。
一、什么是快速幂算法?
快速幂算法,也称为二分幂算法,通过将指数进行二进制拆分,从而减少幂运算的次数,从而提高计算效率。其基本思想是利用指数的二进制表示来降低计算时间复杂度,使得幂运算的时间复杂度从O(n)降低到O(logn)。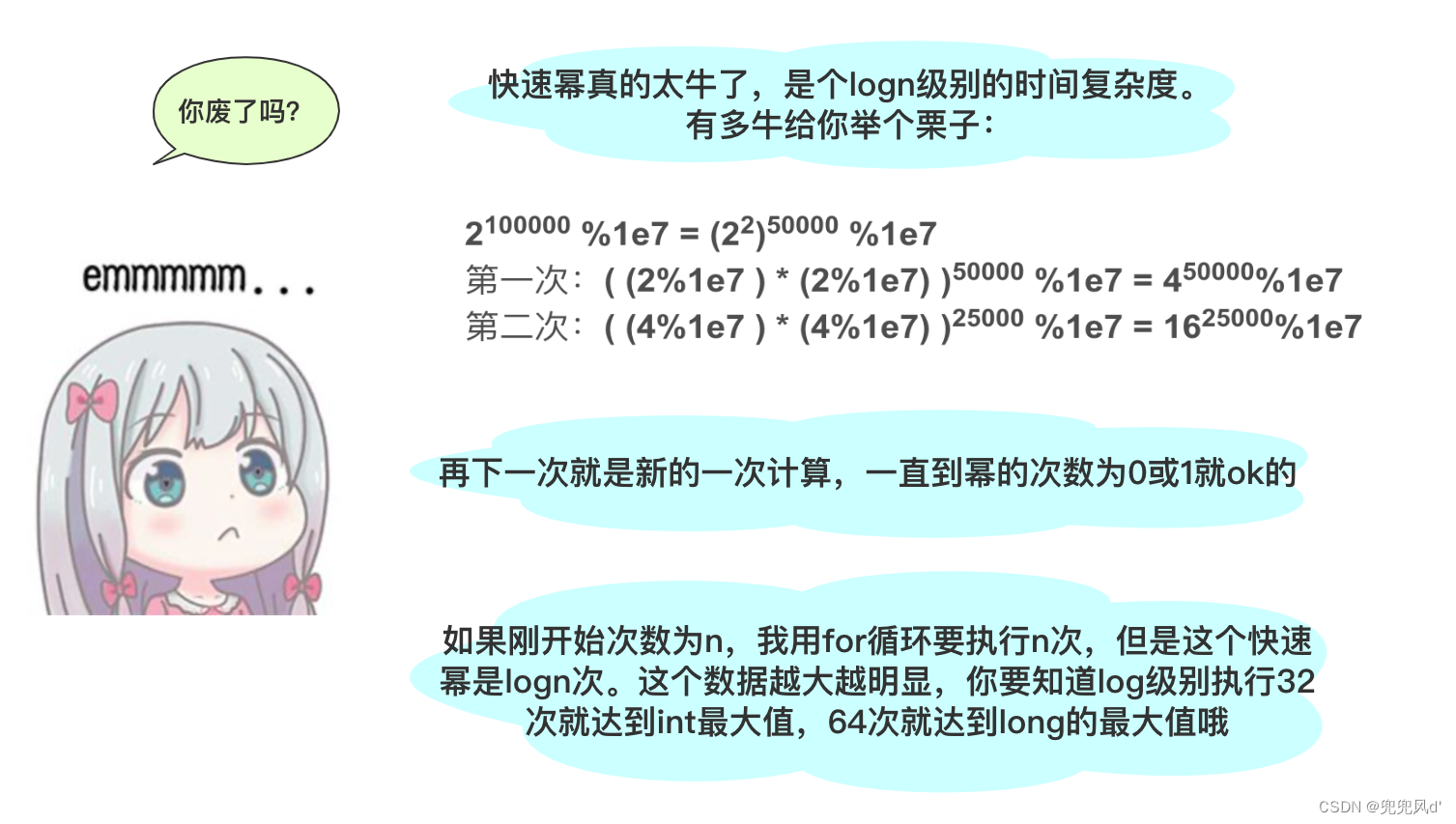
二、快速幂算法的实现
在Java中,我们可以通过递归或迭代的方式来实现快速幂算法。以下是一种简单的迭代实现方法:
public class FastPower {public static long fastPowerIterative(long base, long exponent) {long result = 1;while (exponent > 0) {if (exponent & 1 == 1) {result *= base;}base *= base;exponent >>= 1;}return result;}public static void main(String[] args) {long base = 2;long exponent = 10;long result = fastPowerIterative(base, exponent);System.out.println(base + " raised to the power of " + exponent + " is " + result);}
}
在上面的代码中,fastPowerIterative方法采用迭代的方式实现快速幂算法。我们通过循环将指数exponent拆分为二进制表示,并根据其二进制位的值来更新结果result和底数base,最终得到幂运算的结果。
三、快速幂算法的应用场景
快速幂算法在实际应用中有着广泛的应用,特别是在需要进行大数幂运算或求模运算时,可以显著提高计算效率。以下是一些快速幂算法常见的应用场景:
-
密码学中的应用:在RSA算法等密码学算法中,需要对大数进行幂运算,快速幂算法能够提高加密和解密的效率。
-
数论问题:在数论中,求解大数的幂对某个数取模的问题经常出现,快速幂算法可以快速求解这类问题。
-
动态规划:在一些动态规划问题中,需要计算状态的幂次方,快速幂算法可以优化状态转移的计算过程。
-
图论中的最短路径问题:在一些图论算法中,需要计算邻接矩阵的幂次方,快速幂算法可以加速这类计算。